Codeforces Round #453 (Div. 2)
传送门:http://codeforces.com/contest/902/problem
A. Visiting a Friend
time limit per test 1 second
memory limit per test 256 megabytes
Pig is visiting a friend.
Pig’s house is located at point 0, and his friend’s house is located at point m on an axis.
Pig can use teleports to move along the axis.
To use a teleport, Pig should come to a certain point (where the teleport is located) and choose where to move: for each teleport there is the rightmost point it can move Pig to, this point is known as the limit of the teleport.
Formally, a teleport located at point x with limit y can move Pig from point x to any point within the segment [x; y], including the bounds.
Determine if Pig can visit the friend using teleports only, or he should use his car.
Input
The first line contains two integers n and m (1 ≤ n ≤ 100, 1 ≤ m ≤ 100) — the number of teleports and the location of the friend’s house.
The next n lines contain information about teleports.
The i-th of these lines contains two integers ai and bi (0 ≤ ai ≤ bi ≤ m), where ai is the location of the i-th teleport, and bi is its limit.
It is guaranteed that ai ≥ ai - 1 for every i (2 ≤ i ≤ n).
Output
Print “YES” if there is a path from Pig’s house to his friend’s house that uses only teleports, and “NO” otherwise.
You can print each letter in arbitrary case (upper or lower).
Examples
input
3 5
0 2
2 4
3 5
output
YES
input
3 7
0 4
2 5
6 7
output
NO
Note
The first example is shown on the picture below:
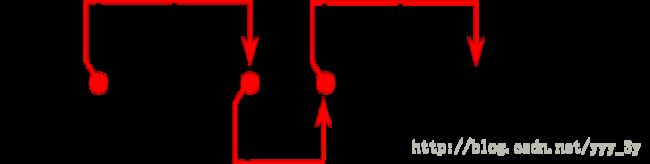
Pig can use the first teleport from his house (point 0) to reach point 2, then using the second teleport go from point 2 to point 3, then using the third teleport go from point 3 to point 5, where his friend lives.
The second example is shown on the picture below:

You can see that there is no path from Pig’s house to his friend’s house that uses only teleports.
题意:起点0,终点m。 现在给你n组a,b。 每组a,b表示可以从a开始到b之内的任意点,看一组样例就很好理解了。
思路: 记录pre_b 为当前能到达的最右边的点。看最后pre _b是否等于m。
#includeB. Coloring a Tree
time limit per test1 second
memory limit per test256 megabytes
inputstandard input
outputstandard output
You are given a rooted tree with n vertices. The vertices are numbered from 1 to n, the root is the vertex number 1.
Each vertex has a color, let’s denote the color of vertex v by cv. Initially cv = 0.
You have to color the tree into the given colors using the smallest possible number of steps. On each step you can choose a vertex v and a color x, and then color all vectices in the subtree of v (including v itself) in color x. In other words, for every vertex u, such that the path from root to u passes through v, set cu = x.
It is guaranteed that you have to color each vertex in a color different from 0.
You can learn what a rooted tree is using the link: https://en.wikipedia.org/wiki/Tree_(graph_theory).
Input
The first line contains a single integer n (2 ≤ n ≤ 104) — the number of vertices in the tree.
The second line contains n - 1 integers p2, p3, …, pn (1 ≤ pi < i), where pi means that there is an edge between vertices i and pi.
The third line contains n integers c1, c2, …, cn (1 ≤ ci ≤ n), where ci is the color you should color the i-th vertex into.
It is guaranteed that the given graph is a tree.
Output
Print a single integer — the minimum number of steps you have to perform to color the tree into given colors.
Examples
input
6
1 2 2 1 5
2 1 1 1 1 1
output
3
input
7
1 1 2 3 1 4
3 3 1 1 1 2 3
output
5
题意:给出1e4个点的树:n-1个数表示节点的父节点,然后n个数表示该节点的颜色。
问要涂多少次才能完成。(初始都为无色)
题解:dfs。建树之后搜一遍,如果当前结点和它的双亲结点一样不需要染色,如果不一样,就需要然后,然后记录下当前的颜色就行。
#includeC. Hashing Trees
time limit per test 2 seconds
memory limit per test 256 megabytes
Sasha is taking part in a programming competition. In one of the problems she should check if some rooted trees are isomorphic or not. She has never seen this problem before, but, being an experienced participant, she guessed that she should match trees to some sequences and then compare these sequences instead of trees. Sasha wants to match each tree with a sequence a0, a1, …, ah, where h is the height of the tree, and ai equals to the number of vertices that are at distance of i edges from root.
Unfortunately, this time Sasha’s intuition was wrong, and there could be several trees matching the same sequence. To show it, you need to write a program that, given the sequence ai, builds two non-isomorphic rooted trees that match that sequence, or determines that there is only one such tree.
Two rooted trees are isomorphic, if you can reenumerate the vertices of the first one in such a way, that the index of the root becomes equal the index of the root of the second tree, and these two trees become equal.
The height of a rooted tree is the maximum number of edges on a path from the root to any other vertex.
Input
The first line contains a single integer h (2 ≤ h ≤ 105) — the height of the tree.
The second line contains h + 1 integers — the sequence a0, a1, …, ah (1 ≤ ai ≤ 2·105). The sum of all ai does not exceed 2·105. It is guaranteed that there is at least one tree matching this sequence.
Output
If there is only one tree matching this sequence, print “perfect”.
Otherwise print “ambiguous” in the first line. In the second and in the third line print descriptions of two trees in the following format: in one line print integers, the k-th of them should be the parent of vertex k or be equal to zero, if the k-th vertex is the root.
These treese should be non-isomorphic and should match the given sequence.
Examples
input
2
1 1 1
output
perfect
input
2
1 2 2
output
ambiguous
0 1 1 3 3
0 1 1 3 2
题意:给你树的高度和每层(从0开始)的节点数。问是否存在非同构树。
如果不存在,输出perfect.
否则输出ambiguous,然后输出一组非同构树。
思路:如果连续两层都大于一,那么一定存在非同构树。
也就是说,如果不存在就是perfect。
主要还是考虑如何构造树,不难想到我们记录下两个连续的非1位置。
第一次输出就全部挂在右边。第二次输出一个挂在左边,剩下的挂在右边。一定是一颗非同构树。
#includeD. GCD of Polynomials
题意: 数学题,凑合凑合搞搞推公式喽~
样例1,(x,1)–>(1,0)
样例2,(x^2-1,x)–>(x,-1)–>(-1,0)
我们推下样例1的上一层。 易得 (x^2+1,x)–>(x,1)–>(1,0) 。感觉和2类似。
再来一层。 (x^3,x^2+1)–>(x^2+1,x)–>(x,1)–>(1,0).
再一层 (x^4+x^2+1,x^3)->(x^3,x^2+1)–>(x^2+1,x)–>(x,1)–>(1,0).
A1 =1 , A2 = X , A3 = x^2 ±1 ,A4 = X^3,A5 = x^4+x^2+1。
由此可以推论得递推式: Ai = Ai−1 * x ± Ai−2 (i ≥2 )
即:n的系数为n-1右移一位加上n-2的系数
这里用vector 存会方便很多。
vector.insert(pos,elem); //在pos位置插入一个elem元素的拷贝,返回新数据的位置。
vector.insert(pos,n,elem); //在pos位置插入n个elem数据,无返回值。
vector.insert(pos,beg,end); //在pos位置插入[beg,end)区间的数据,无返回值
#include