Dijkstra算法图解

最短路径问题

从图中的某个顶点出发到达另外一个顶点的所经过的边的权重和最小的一条路径，称为最短路径。

解决方法：

• Floyd算法
• Bellman-Ford算法
• SPFA算法
• Dijkstra算法

Djikstra算法

算法特点：Dijkstra算法适用于计算正权图（边权为正）上的单源最短路，即从单个源点出发，到所有节点的最短路。该算法同时适用于有向图和无向图。

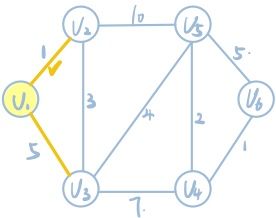
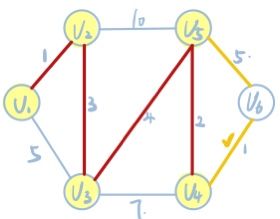
算法思路：从已确定最短路径的节点Vi出发，找到其中权值最小的边，如果原点到Vi的权值和加Vi到Vj的权值小于已知原点到Vj的权值和，则将原点到Vi的权值和加Vi到Vj的权值作为原点到Vj的最小权和。（讲的有点不是特别清楚，看图分析）

1.已知V1为原点，则从V1出发，找到其中权值最小的边。即V1到V2这条边，权值为2，则将V1->V2确定为原点到V2的最短路径。同时记V1到V3的权值为5，虽然不一定是最短路径，但要记录。

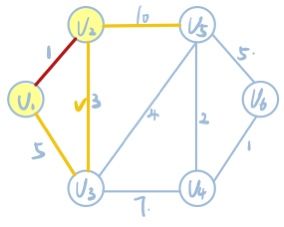
2.已确定V1和V2的最短路径，则V2出发，找到其中权值最小的边。即V2到V3这条边，且V1->V2->V3的权值和小于V1->V3的权值，即1+3<5，则将V1->V2->V3确定为原点到V3的最短路径。同时记V2->V5的权值10，V1->V2->V5的权值和为11，同理虽然不一定为最短路径，但要记录。

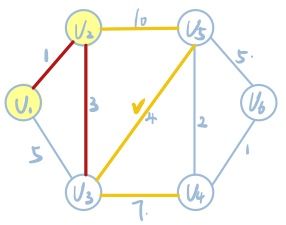
4已确定V1、V2和V3的最短路径，则V3出发，找到其中权值最小的边。即V3到V5这条边，且V1->V2->V3->V5的权值和为8，小于上一步骤中V1->V2->V5这条路径。则将V1->B2->V3->V5确定为原点到V5的最短路径。同时记V1->V2->V3->V4的权值和为11.

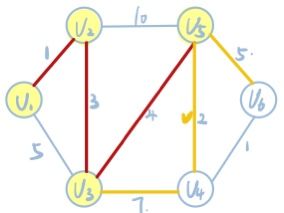
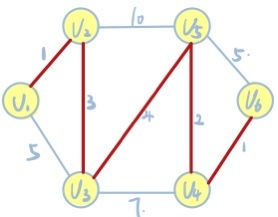
5.已确定V1、V2、V3和V5的最短路径，则从V5出发，找到权值最小的边。即V5->V4这条边，且V1->V2->V3->V5->V4的权值和为10，小于上衣步骤中V1->V2->V3->V4这条路径。则将V1->V2->V3->V5->V4确定为原点到V4的最短路径。同时记V1->V2->V3->V5->V6的权值和为13.

6.已确定V1、V2、V3、V5和V4的最短路径，则从V4出发，找到权值最小的边。即V4->V6这条边，且V1->V2->V3->V5->V4->V6的权值和为11，小于上一步骤中V1->V2->V3->V5->V6这条路径。则将V1->V2->V3->V5->V4->V6确定为原点到V6的最短路径。至此，所有节点的最短路径都已确定完毕。

为实现这个思路，我们需要定义一个结构体用来存放每一条边，并且记录好起点、终点和权值。

struct edge{
	int from, to, w;//起点，终点，权值 
	edge(int u, int v, int d){ from=u;to=v;w=d;}
};
vectore[num];//e[i]用于存放以节点i为起点的所有边。

同时再定义一个结构体用来存放节点编号以及到原点的权值和。

struct node{
	int id, dist;//节点编号，到原点的距离
	node(int u, int d){ id=u;dist=d;}
	bool operator <(const node &a)const
	{	return dist > a.dist;}//排序规则：按dist从小到大排序 
};

 定义三个数组分别记录每个节点的前驱节点、到原点的权值和、是否已确定为最短路径。

int pre[num];//前驱节点
int dis[num];//到原点权值和
int done[num];//是否已为最短路径

 接下来就是最重要的Dijkstra函数的一个实现过程，思路已在前面图中展现，代码通过注释配合图解应该能够理解。

邻接表存图dijkstra。

#include
#include
#include
#include
using namespace std;
const int inf = 0x3f3f3f3f;
const int num = 1001;

struct edge{
	int from, to, w;//起点，终点，权值 
	edge(int u, int v, int d){ from=u;to=v;w=d;}
};
vectore[num];

struct node{
	int id, dist;//节点编号，到原点的距离
	node(int u, int d){ id=u;dist=d;}
	bool operator <(const node &a)const
	{	return dist > a.dist;}//排序规则：按dist从小到大排序 
};

int n, m, s;
int pre[num];
int dis[num];
int done[num];
//分别记录节点i的前驱节点，到原点的距离，是否已取得最短距离

void print_path(int u, int v){//输出从点u到点v的最短距离路径 
	if(u==v){	printf("%d", u);return;}
	print_path(u, pre[v]);
	printf("->%d", v);
} 

void dijkstra(){
	for(int i=1; i<=n; i++){
		dis[i] = inf;
		done[i] = 0;
	}
	s = 1;
	dis[s] = 0;
	
	priority_queueq;//按dist从小到达排序的优先队列 
	q.push(node(s, dis[s]));
	
	while(!q.empty()){
		//取出队列中的第一个node（含节点编号和距离） 
		node u = q.top();
		q.pop();
		
		if(done[u.id])	continue;//若节点u.id未已取得最短路径，再执行后续操作 
		done[u.id] = 1;
		
		for(int i=0; i u.dist + y.w){
				dis[y.to] = u.dist + y.w;
				q.push(node(y.to, dis[y.to]));
				pre[y.to] = u.id;
			}
		}
	}
}

int main(){
	while(~scanf("%d%d", &n, &m) && n && m){//n个节点，m条边 
		for(int i=1; i<=n; i++)	e[i].clear();//清空所有边
		
		while(m--){
			int u, v, w;
			scanf("%d%d%d", &u, &v, &w);
			e[u].push_back(edge(u, v, w));
			e[v].push_back(edge(v, u, w));
			//（无向图）将边分别插入e[u]、e[v] 队列中 
		} 
		
		dijkstra(); 
	}
	return 0;
}

链式前向星存图dijkstra（恢复注释代码即hdu1595的解）

#include 
#include 
#include 
using namespace std;
const int inf = 0x3f3f3f3f;
const int maxm = 1e6;
const int maxn = 1006;

struct edge{
	int to, w, next;
} e[maxm];

struct node{
	int id, s;
	node(int a,int b){id = a;s = b;}
	bool operator <(const node a)const{
		return a.s < s;}
};

int n, m, cnt;
int id[maxm];					//最短路上经过的边的序号
int vis[maxn];					//标记数组
int head[maxm];					//链式前向星头结点
int dist[maxn];					//距离数组
int pre[maxn];					//前驱数组
priority_queueq;

void addedge(int x,int y,int w){
	e[cnt].to = y;
	e[cnt].w = w;
	e[cnt].next = head[x];
	head[x] = cnt++;
}

void clear_set(){
	for (int i = 1; i <= n; i++)
		vis[i] = 0;
	fill(dist, dist + maxn, inf);
	while(!q.empty())
		q.pop();
}

void init(){
	cnt = 0;
	for (int i = 1; i <= n; i++){
		head[i] = pre[i] = -1;
		id[i] = 0;
	}
}

int dijkstra(int flag,int n){
	clear_set();
	dist[1] = 0;
	q.push(node(1, 0));
	while(!q.empty()){
		node p = q.top();
		q.pop();
		if(vis[p.id])
			continue;
		vis[p.id] = 1;
		for(int i = head[p.id]; ~i; i = e[i].next){				//head[p.id]访问的是边的编号 
			edge t = e[i];
			if(!vis[t.to] && dist[t.to] > dist[p.id] + t.w){			//松弛 
				dist[t.to] = dist[p.id] + t.w;
				q.push(node(t.to,dist[t.to]));
				if(flag == 1){					
					pre[t.to] = p.id;				//记录前驱节点 
					// id[t.to] = i;					//记录到达这个点的边的序号 
				}
			}
		}
	}
	if(dist[n] == inf)
		return -1;
	return dist[n];
}

int main(){
	while(~scanf("%d%d",&n,&m)){
		init();
		for(int i = 0; i < m; i++){
			int x, y, z;
			scanf("%d%d%d", &x, &y, &z);
			addedge(x, y, z);
			addedge(y, x, z);
		}
		int ans = dijkstra(1,n);
		// int t = n;
		// while(t != -1){					//枚举最短路经过的所有边，分别进行一次"删除"
		// 	int w = e[id[t]].w;
		// 	e[id[t]].w = inf;
		// 	ans = max(ans, dijkstra(0, n));
		// 	e[id[t]].w = w;	
		// 	t = pre[t];
		// }
		printf("%d\n",ans);
	}
	return 0;
}

 

（文末补充，如果有哪里写的不对或是表述不清的地方，欢迎指出。