Codeforces Round #498 (Div.3)
目录
A - Adjacent Replacements
B - Polycarp's Practice
C - Three Parts of the Array
D - Two Strings Swaps
E - Military Problem
F - Xor-Paths
A - Adjacent Replacements
题意:
有一个含有n个元素的数列, 1 <= ai <=1e9,求数列进行下列操作后的结果。
操作从上往下执行
将数列中所有的1变成2
将数列中所有的2变成1
...
将数列中所有的 1e9-1 变成 1e9
将数列中所有的 1e9 变成 1e9-1
题解:
每两次操作,奇数不变,偶数变为比原来小1的奇数
#include
#include
#include
using namespace std;
const int maxn = 1e3 + 20;
typedef long long LL;
int n,a[maxn];
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) {
int x;
scanf("%d",&x);
if(i-1) printf(" ");
if(x&1) printf("%d",x);
else printf("%d",x-1);
}
printf("\n");
return 0;
}
B - Polycarp's Practice
题意:
将一个含有n个元素的数列分为不相交的k块,每块要连续,求出每块的最大值之和,以及从左到右输出划分后每块的元素个数
题解:
因为可以一个数作为一个区间,所以前k大的数必然可以分到不同的k个区间中去
所以只要先进行一个排序,找到前k大的数的位置,再按位置来划分即可
#include
#include
#include
#include
using namespace std;
const int maxn = 2e3 + 20;
typedef long long LL;
int n,k,pos[maxn];
struct node{
int a, id;
friend bool operator < (node a,node b){
return a.a > b.a;
}
}a[maxn];
int main()
{
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++) {
scanf("%d",&a[i].a);
a[i].id = i;
}
sort(a+1, a+1+n);
int mx = 0;
for(int i=1;i<=k;i++) {
mx += a[i].a;
pos[a[i].id] = 1;
}
int flag = 0, cnt = 0;
printf("%d\n",mx);
if(k==1){
printf("%d\n",n);
return 0;
}
for(int i=1;i<=n;i++){
cnt ++;
if(pos[i]){
if(flag) printf(" ");
printf("%d",cnt);
flag ++;
cnt = 0;
if(flag == k-1) {
flag = i;
printf(" %d\n", n-flag);
break;
}
}
}
return 0;
}
C - Three Parts of the Array
题意:
将一个数列分为不相交连续的3块,可以为空,三块的元素和分别为sum1,sum2,sum3
求 sum1 = sum3 的最大值
题解:
直接遍历所有的找到最大的即可
#include
#include
#include
#include
using namespace std;
const int maxn = 2e5 + 20;
typedef long long LL;
LL n,k,a[maxn],sum[maxn];
int main()
{
scanf("%lld",&n);
for(int i=1;i<=n;i++) {
scanf("%lld",&a[i]);
sum[i] = sum[i-1] + a[i];
}
LL l = 1, r = n, mx = 0;
while(l= r) break;
if(sum[l] == sum[n] - sum[r-1]) mx = sum[l];
l ++;
}
printf("%lld\n",mx);
return 0;
}
D - Two Strings Swaps
题意:
有两个长度均为n的字符串a,b
对a,b串有下列三种操作( i = 1, 2, .., n ):
1、将 a[i] 与a[n-i+1] 互换
2、将b[i] 与 b[n-i+1] 互换
3、将a[i] 与 b[i] 互换
但是有可能经过多次上述操作后依旧不能使得串a与串b相等,所以请你求出最少改变字符串a中的几个字符,才能使得新的串a和串b经过多次操作后完全相同。
题解:
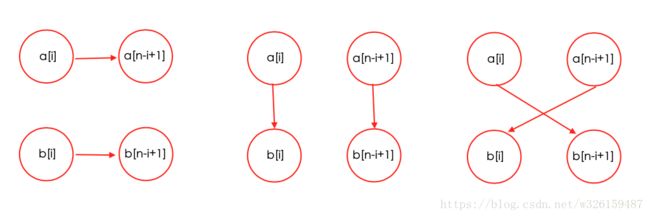
因为i与n-i+1恰好是头尾的对称位置,总结操作可以得出结论:a[i], a[n-i+1], b[i], b[n-i+1]四个字符是可以任意交换的
即要使得ab两串可以完全相同,即每组字母都要有两对相同的字母才有可能。
而字母匹配的方式有如下三种
从三种中找出最大的相同的个数cnt,然后 2-cnt 就是需要改变的个数,因为一对不一样只需要改变其中一个字母为另一个即可
需要注意的是第一种匹配的方式,由于只能够改变a串且在改变前不可交换ab串,所以当a串两个相同但b串两个不同时不能只改变一个b串中的字母,因为b串不可改变。
所以只能变a串,有两种可能:
1、a串的字母与b的两个均不同; 这样的这种匹配方式就要变两次,即令cnt = 0
2、a串的字母与b的其中一个相同; 那样的话只用改变a中的一个即可,令cnt = 1
但是其实后面两种包含了第二种可能,所以只需要把最大相同个数置零即可
#include
#include
#include
using namespace std;
const int maxn = 1e5 + 10;
int n, ans;
char a[maxn], b[maxn];
int same(char a,char b){return a == b;}
int add(int p1, int p2){
int ans = same(a[p1],a[p2]) + same(b[p1],b[p2]);
if(a[p1]==a[p2] && b[p1]!=b[p2]) ans = 0; // 只能改a串不能改b串
ans = max(ans, same(a[p1],b[p1]) + same(a[p2],b[p2]));
ans = max(ans, same(a[p1],b[p2]) + same(a[p2],b[p1]));
return 2-ans;
}
int main()
{
scanf("%d%s%s", &n, a+1, b+1);
for(int i=1;i<=n/2;i++) ans += add(i, n-i+1);
if(n%2==1 && a[n/2+1] != b[n/2+1]) ans ++;
printf("%d\n",ans);
return 0;
}
E - Military Problem
题意:
有一颗含有n个节点的树,1为根结点,给出其余节点的父亲节点,有m个询问,每个询问有两个数字ui,ki
对每个询问输出结果。
询问的意思就是以ui作为深度优先搜索的起点,求这次搜索的到的第ki个节点是哪一个,若不存在输出-1。
思路:
由DFS的性质可以知道,以u为起点进行dfs第k个点A,在以1作为起点进行dfs中的序号为 k - 1 + dfn[u]
其中dfn[u] 为以1作为起点进行DFS的节点为u的序号
另外还有判断是否有第k个点,只要在DFS的过程中记录每个点回溯时其下方最后一个点的dfn即可,然后进行比较可以判断是否存在第k个点。
#include
#include
#include
#include
#include
using namespace std;
const int maxn = 2e5 + 20;
typedef long long LL;
int n,k,x,y,dfn[maxn],id[maxn],ed[maxn];
vectorG[maxn];
int sz = 0;
void dfs(int x){
dfn[x] = ++sz; // 记录当前dfn
id[sz] = x; // 记录dfn为sz 对应的数值为多少,便于查找
for(int i=0;ied[x]) printf("-1\n"); // 判断是否在x点下方
else printf("%d\n",id[to]);
}
return 0;
}
F - Xor-Paths
题意:
有一个n行m列的矩阵,矩阵的每个点都有各自的值aij,求从(1,1)走到(n,m)路径上的所有值的异或等于k的路径条数。
题解:
直接遍历所有路径复杂度过高
所以要利用到异或的性质,即:a ^ b ^ c ^ d = (a^b) ^ (c^d) 和 a^b = k => a = k ^ b
然后将整个矩阵分割成两块(要尽量对称),对(1,1) 和 (n,m)分别进行一次DFS搜索,搜索的终点为距离(1,1) , (n,m)相差最小的点,即 x - 1 + y - 1 = n - x + m - y 得到等式 x+y = (n+m)/2 + 1
这样每次DFS的最高也不会超过2^20,大大减少了时间
然后就可以先从(1,1)开始,记录满足 x+y = (n+m)/2 + 1 的节点的所有异或值以及条数mp[x][val]
再从(n,m)开始,每满足 x+y = (n+m)/2 + 1 就增加一次答案的贡献,mp[x][当前路径总异或值^k^a[x][y]]
因为a[x][y]用了两次所以再异或一次来抵消掉
#include
#include
#include
#include
#include