搜索初步1
搜索算法是利用计算机的高性能来有目的的穷举一个问题解空间的部分或所有的可能情况,从而求出问题的解的一种方法。现阶段一般有枚举算法、深度优先搜索、广度优先搜索、A*算法、回溯算法、蒙特卡洛树搜索、散列函数等算法。
目录:
1.深度优先搜索(DFS)
2.广度优先搜索(BFS)
3.剪枝
3.经典例题
1.深度优先搜索
深度优先搜索,又叫DFS,顾名思义就是按照深度优先的顺序对于“问题状态空间”进行搜索的算法。
深度优先搜索的核心思想
举例说明一下:下图是一个无向图,如果我们从A点发起深度优先搜索,则我们可能得到如下的一个访问过程:A->B->E(没有路了!回溯到A)->C->F->H->G->D(没有路,最终回溯到A,A也没有未访问的相邻节点,本次搜索结束)。纯粹的不撞南墙不回头。

基本算法框架:
int search(int k) {
if(到目的地)
输出解;
else {
for(int i=1;i<=算符总数;i++) {
if(满足条件) {
保存条件
search(k+1);
恢复:保存条件之前的结果(回溯一步)
}
}
}
}
回溯:主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。不能把当前的条件保留下来影响后面的搜索(当然,有一些条件是可以不用改的,只要你能保证它不会影响后续的搜索或者它在后续会被覆盖掉)。
2.广度优先搜索
广度优先搜索,又称宽度优先搜索或者BFS,是一种最简便的图的搜索算法之一。
广度优先搜索的核心思想
从初始节点开始,应有算符生成第一层节点,检查目标节点是否在这些节点中,若没有,再用产生规则将所有的第一层的节点逐一延展,得到第二层节点,并逐一检查第二层中是否有目标节点,若没有…依次检查下去,直到发现目标节点。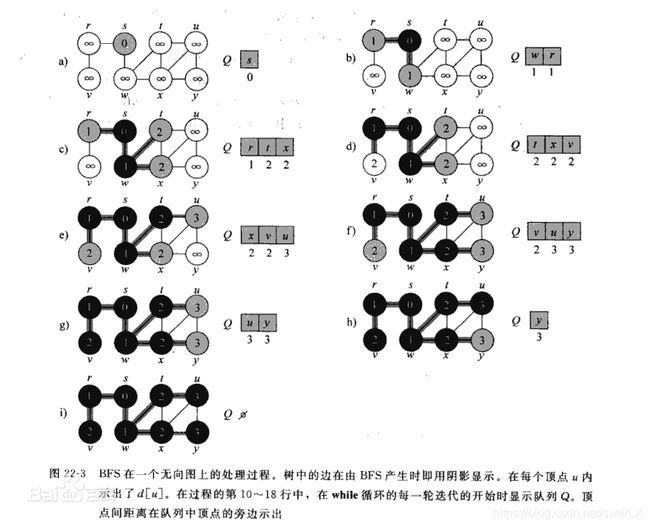
基本算法框架:
举个例子:我们从(bx,by)开始,要在一个长宽分别为n和m的矩阵中搜索一个节点(xx,yy)。
int ex[4]={1,0,-1,0};
int ey[4]={0,1,0,-1};
void BFS(int bx,int by) {
vis[bx][by]=1;
queue a,b;
a.push(bx),b.push(by);
while(a.size()) {
int x=a.front(),y=b.front();
a.pop(),b.pop();
if(x==xx && y==yy) {
printf("YES");
return ;
}
for(int i=0;i<4;i++) {
int nx=x+ex[i],ny=y+ey[i];
if(nx>0 && ny>0 && nx<=n && ny<=m && vis[nx][ny]==0) {
vis[nx][ny]=1;
a.push(nx),b.push(ny);
}
}
}
printf("NO");
return ;
}
DFS和BFS的区别:
DFS可以说是碰运气似的乱搜索,可能会出现答案就在身边,而却在其他地方搜索了很久,而且第一时间找到的答案不一定就是最佳答案,所以必须要将所有的路径都搜索完。
而BFS就完全不同了,它就是稳打稳扎,一步一步慢慢向前。而且第一时间搜索到的答案一定是最佳答案。但当答案离初始节点很远时,时间和空间就会大幅度提高。
剪枝
1.优化搜索顺序
在一些搜索问题中,搜索树的各个层次、各个分支之间的顺序是不固定的。不同的搜索顺序会产生不同的搜索树,会导致搜索效率变高。
2.排除等效冗余
当我们能判断从当前节点的不同分支搜索下去结果是一样的,那我们搜索一次就可以了。
3.可行性剪枝
如果我们可以判断当前节点搜索下去绝对找不到结果,我们就不用找了。
4.最优性剪枝
在最优化问题中,如果当前花费的代价已经超过了当前搜索到的最优解,我们就可以不在搜索下去了。
5.记忆化
可以记录每个状态的搜索结果,再重复搜索的时候直接检索并返回。这就好比我们用DFS时,标记一个节点是否已经被访问过。
经典例题
1.特殊的质数肋骨 Superprime Rib
题目描述
农民约翰的母牛总是产生最好的肋骨。你能通过农民约翰和美国农业部标记在每根肋骨上的数字认出它们。农民约翰确定他卖给买方的是真正的质数肋骨,是因为从右边开始切下肋骨,每次还剩下的肋骨上的数字都组成一个质数。
举例来说:7 3 3 1 全部肋骨上的数字7331 7331 是质数;三根肋骨 733 733是质数;二根肋骨73 73是质数;当然,最后一根肋骨7 7也是质数。7331被叫做长度4的特殊质数。
写一个程序对给定的肋骨的数目n,求出所有的特殊质数。1 不是质数。
【数据范围】
对于100%的数据,1<= n <=8
这就是一个简单的DFS板题
代码1:
#include
using namespace std;
int n, sum = 1;
bool o(int t) {
for (int i = 2; i <= sqrt(t); i++) {
if (t % i == 0)
return 0;
}
return 1;
}
bool yu(int t) {
for (int i = 1; i <= n; i++) {
if (o(t) == 0 || t == 1)
return 0;
t /= 10;
}
return 1;
}
void cha(int book) {
if (book >= sum * 10)
return;
if (yu(book))
printf("%d\n", book);
cha(book + 1);
return;
}
int main() {
scanf("%d", &n);
for (int i = 1; i < n; i++) sum *= 10;
cha(sum);
return 0;
}
非常完美的超时了!
确实,时间复杂度太大了
代码2:
#include
using namespace std;
int n, sum = 1, book;
bool v[100000005];
bool yu(int t) {
for (int i = 1; i <= n; i++) {
if (v[t] == 1)
return 0;
t /= 10;
}
return 1;
}
void primes() {
for (int i = 2; i <= book; i++) {
if (v[i])
continue;
if (yu(i) == 1 && i >= sum && i <= book)
printf("%d\n", i);
for (int j = i; j <= book / i; j++) v[i * j] = 1;
}
return;
}
int main() {
v[1] = 1;
scanf("%d", &n);
int t = 10;
for (int i = 1; i < n; i++) {
sum *= 10;
book += t * 9;
t *= 10;
}
book += 9;
primes();
return 0;
}
这次用了Eratosthenes筛法
能过关!
但我们其实能根据代码1来打表
代码3:
#include
using namespace std;
int ans[9][20]={{},{0,2,3,5,7},{0,23,29,31,37,53,59,71,73,79},{0,233,239,293,311,313,317,373,379,593,599,719,733,739,797},{0,2333,2339,2393,2399,2939,3119,3137,3733,3739,3793,3797,5939,7193,7331,7333,7393},{0,23333,23339,23399,23993,29399,31193,31379,37337,37339,37397,59393,59399,71933,73331,73939},{0,233993,239933,293999,373379,373393,593933,593993,719333,739391,739393,739397,739399},{0,2339933,2399333,2939999,3733799,5939333,7393913,7393931,7393933},{0,23399339,29399999,37337999,59393339,73939133}};
int book[9]={0,4,9,14,16,15,12,8,5};
int main() {
int n;
scanf("%d",&n);
for(int i=1;i<=book[n];i++)
printf("%d\n",ans[n][i]);
return 0;
}
不要小看了打表,关键时刻可以救你命!
2.八皇后问题
题目描述
在国际象棋棋盘上放置八个皇后,要求每两个皇后之间不能直接吃掉对方。
样例输出:
No. 1
1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 1
0 1 0 0 0 0 0 0
0 0 0 1 0 0 0 0
0 0 0 0 0 1 0 0
0 0 1 0 0 0 0 0
No. 2
1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 0 1 0 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 1
0 1 0 0 0 0 0 0
0 0 0 0 1 0 0 0
0 0 1 0 0 0 0 0
No. 3
1 0 0 0 0 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 1
0 0 1 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 0 1 0 0 0 0
0 1 0 0 0 0 0 0
0 0 0 0 1 0 0 0
No. 4
1 0 0 0 0 0 0 0
0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 1
0 0 0 0 0 1 0 0
0 0 1 0 0 0 0 0
0 0 0 0 0 0 1 0
0 1 0 0 0 0 0 0
0 0 0 1 0 0 0 0
No. 5
0 0 0 0 0 1 0 0
1 0 0 0 0 0 0 0
0 0 0 0 1 0 0 0
0 1 0 0 0 0 0 0
0 0 0 0 0 0 0 1
0 0 1 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 0 1 0 0 0 0
No. 6
0 0 0 1 0 0 0 0
1 0 0 0 0 0 0 0
0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 1
0 1 0 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 1 0 0 0 0 0
0 0 0 0 0 1 0 0
No. 7
0 0 0 0 1 0 0 0
1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1
0 0 0 1 0 0 0 0
0 1 0 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 1 0 0 0 0 0
0 0 0 0 0 1 0 0
No. 8
0 0 1 0 0 0 0 0
1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 1
0 1 0 0 0 0 0 0
0 0 0 1 0 0 0 0
0 0 0 0 0 1 0 0
No. 9
0 0 0 0 1 0 0 0
1 0 0 0 0 0 0 0
0 0 0 1 0 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 1
0 1 0 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 1 0 0 0 0 0
…以下省略
这也是一道DFS
但我们怎么来记忆化呢?
我们可以分析分析:
皇后是可以杀一个‘米’字型
横竖不用担心
但撇怎嘛办?
撇我们可以发现每一个节点的x和y相加结果相同
那捺呢?
捺则是x和y相减的结果相同
so
代码1:
#include
using namespace std;
int sum = 1;
bool ans[10][10], shu[10], zx[30], yx[30]; // z j,y j
void print() {
printf("No. %d\n", sum);
sum++;
for (int i = 1; i <= 8; i++) {
for (int j = 1; j <= 8; j++) printf("%d ", ans[i][j]);
printf("\n");
}
return;
}
void cha(int t) {
if (t == 9) {
print();
return;
}
for (int i = 1; i <= 8; i++) {
if (shu[i] == 0 && zx[t - i + 8] == 0 && yx[t + i] == 0) {
shu[i] = 1, zx[t - i + 8] = 1, yx[t + i] = 1;
ans[t][i] = 1;
cha(t + 1);
ans[t][i] = 0;
shu[i] = 0, zx[t - i + 8] = 0, yx[t + i] = 0;
}
}
return;
}
int main() {
cha(1);
return 0;
}
灰常完美,所有的点都炸了
怎么会这样呢?
我们来观察一下样例,好像样例没有规律耶?
但仔细一瞧,细细一品
这样例中的t应该是列,而我们是行
于是正解该这样:
#include
using namespace std;
int sum;
bool ans[10][10], shu[10], zx[30], yx[30];
void print() {
sum++;
printf("No. %d\n", sum);
for (int i = 1; i <= 8; i++) {
for (int j = 1; j <= 8; j++) printf("%d ", ans[j][i]);
printf("\n");
}
return;
}
void cha(int t) {
if (t == 9) {
print();
return;
}
for (int i = 1; i <= 8; i++) {
if (shu[i] == 0 && zx[t - i + 8] == 0 && yx[t + i] == 0) {
shu[i] = 1, zx[t - i + 8] = 1, yx[t + i] = 1;
ans[t][i] = 1;
cha(t + 1);
ans[t][i] = 0;
shu[i] = 0, zx[t - i + 8] = 0, yx[t + i] = 0;
}
}
return;
}
int main() {
cha(1);
return 0;
}
只用输出时改一下就可以了!!!
3.木棒
题目描述
乔治拿来一组等长的木棒,将它们随机地砍断,使得每一节木棍的长度都不超过50个长度单位。然后他又想把这些木棍恢复到为裁截前的状态,但忘记了初始时有多少木棒以及木棒的初始长度。
请你设计一个程序,帮助乔治计算木棒的可能最小长度。
每一节木棍的长度都用大于零的整数表示。
注意: 数据中可能包含长度大于50的木棒,请在处理时忽略这些木棒。
输入包含多组数据,每组数据包括两行。
第一行是一个不超过64的整数,表示砍断之后共有多少节木棍。
第二行是截断以后,所得到的各节木棍的长度。
在最后一组数据之后,是一个零。
输出格式
为每组数据,分别输出原始木棒的可能最小长度,每组数据占一行。
我们可以从小到大枚举原始木棒的长度len(也就是枚举答案)。当然,len应该是所有木棒长度中和sum的约数,并且原始木棒长度的根数cnt就等于sum/len。
对于每个len,我们可以依次搜索每根原始木棒有哪些木棒拼成。则搜索所面对的状态包括:已经拼好的根数,正在拼的木棒的长度,每根木棒的使用情况。在每个状态下,我们就从尚未使用的木棒中选一根来尝试拼。
但这个算法效率比较低,要考虑剪枝:
1.优化搜索顺序:
将木棒长度从大到小排序,优先使用长的木棒
2.排除等效冗余:
(1)可以限制先后加入一根原始木棒是递减的
(2)对于当前原始木棒,记录最近一次尝试的木棒。如果搜索失败,就回溯,不在尝试(因为必然也失败)
(3)如果当前原始木棒尝试拼入的第一根木棒返回失败,则直接判断当前分支失败。
(4)如果当前原始木棒中拼入一根木棒后,木棒恰好拼接完整,并且接下来拼接剩余原始木棒失败,则整个失败。
代码:
#include
using namespace std;
int a[105],c[105],n,len,ans,j;
bool cmp(int x,int y) {
return x>y;
}
int cha(int yp,int yc,int l) {
if(yp==ans+1)
return 1;
if(yc==len)
return cha(yp+1,0,1);
int k=0;
for(int i=l;i<=j;i++) {
if(c[i]==0 && yc+a[i]<=len && k!=a[i]) {
c[i]=1;
if(cha(yp,yc+a[i],i+1)==1)
return 1;
c[i]=0;
k=a[i];
if(yc==0 || yc+a[i]==len)
return 0;
}
}
return 0;
}
int main() {
while(scanf("%d",&n) && n) {
int sum=0,v=0,x;
j=0;
for(int i=1;i<=n;i++) {
scanf("%d",&x);
if(x<=50) {
a[++j]=x;
sum+=a[j];
v=(v>a[j]?v:a[j]);
}
}
sort(a+1,a+j+1,cmp);
for(len=v; len<=sum; len++) {
if(sum%len==0) {
memset(c,0,sizeof(c));
ans=sum/len;
if(cha(1,0,1)) {
printf("%d\n",len);
break;
}
}
}
}
return 0;
}