线性代数系列讲解第一篇 矩阵

1.矩阵

先简单讲解什么是矩阵，给小白们一个印象。矩阵可以是说从解方程组得来，为什么这么说呢，先举个例子：
$$\{\begin{array}{c}2x-y=0\\ -x+2y=3\end{array}$$
我们可以将其写成
$$\left[\begin{array}{cc}2& -1\\ -1& 2\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{c}0\\ 3\end{array}\right]$$
这里可能涉及到矩阵的乘法，我们先不管，后面我们进行详解，这里的第一个矩阵为
$$\left[\begin{array}{cc}2& -1\\ -1& 2\end{array}\right]$$
如果有个人跟你说第一行第二列是啥，那么我们得规定什么是行什么是列。请见下图

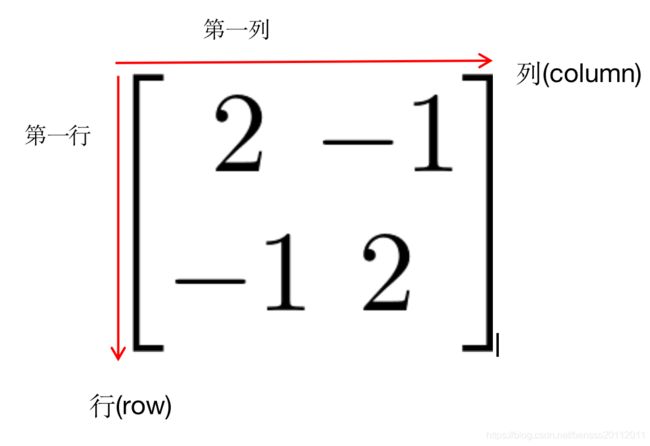
则我们可以回答了这个矩阵第一行第二列是-1啦，讲完了什么是矩阵了，那就来讲讲对矩阵的理解。
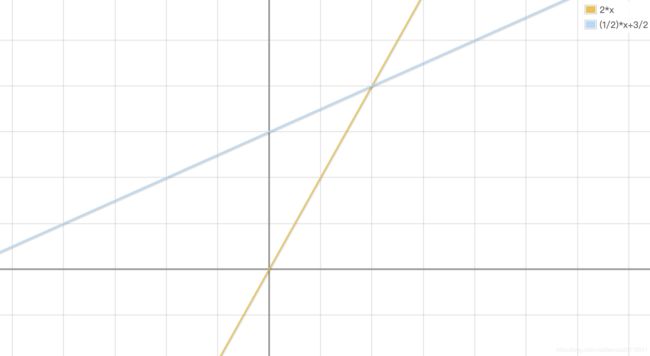
行图像：从行的角度看就是行的线性组合(方程组形式)
$$\begin{array}{c}2x-y=0\\ -x+2y=3\end{array}$$
可以这样看，矩阵的第一行是$\left[\begin{array}{cc}2& -1\end{array}\right]$,2的意思是我们需要$\left[\begin{array}{c}x\\ y\end{array}\right]$中2倍的第一行，-1的意思是我们需要$\left[\begin{array}{c}x\\ y\end{array}\right]$中-1倍的第二行，就是$2x-y=0$
下图为行图像

列图像：从列的角度看就是列的线性组合
$$x\left[\begin{array}{c}2\\ -1\end{array}\right]+y\left[\begin{array}{c}-1\\ 2\end{array}\right]=\left[\begin{array}{c}0\\ 3\end{array}\right]$$
可以这样看，$\left[\begin{array}{c}x\\ y\end{array}\right]$中第一行为$x$表示我们需要 $\left[\begin{array}{cc}2& -1\\ -1& 2\end{array}\right]$中$x$倍的第一列即$x\left[\begin{array}{c}2\\ -1\end{array}\right]$
当x=1，y=2时候如下图

我们可以通过以上看出：
1.以矩阵$\left[\begin{array}{cc}2& -1\\ -1& 2\end{array}\right]$来看，如果我们想对这个矩阵各列进行线性组合怎么办，我们只需要在它右边乘上一个矩阵即可。
2.以矩阵$\left[\begin{array}{c}x\\ y\end{array}\right]$来看，我们想对这个矩阵各行线性组合怎么办，我们只需要在它左边乘上一个矩阵即可。

总结：对于一个矩阵来说，我们想对其行进行线性组合，只需要在它左边乘上矩阵，想对其列进行线性组合，在它右边乘上矩阵。

2.矩阵的乘法

(1).总的公式$$c_{ij}=a_{i1}{b}_{1j}+a_{i2}{b}_{2j}+\cdots +a_{in}{b}_{nj}=\sum _{k=1}^n{a}_{ik}{b}_{kj}$$

先解释一下下标的问题，$c_{ij}$表示$C$中第i行第j列元素。
设$A$为$m$x$n$的矩阵,$B$为$n$x$p$的矩阵，则矩阵$A$与矩阵$B$相乘得到矩阵$C$，如下图
$$\underset{A}{{\left[\begin{array}{ccc}& & \\ & & \\ a_{31}& a_{32}& \cdots \\ & & \end{array}\right]}_{m\ast n}}\underset{B}{{\left[\begin{array}{ccccc}& & & b_{14}& \\ & & & b_{24}& \\ & & & ⋮& \end{array}\right]}_{n\ast p}}=\underset{C}{{\left[\begin{array}{ccccc}& & & & \\ & & & & \\ & & & c_{34}& \\ & & & & \end{array}\right]}_{m\ast p}}$$
我们要注意，$A$中第二个数要与B中第一个数相等，即n，不然会出现无法相乘的情况。
我们可以看出$A$中的第三行和$B$中的第二列得出$C$中的$c_{34}$
$$\begin{gathered} c_{34}=(A的第三行)\cdot (B的第四列) \\ =a_{13}{b}_{14}+a_{32}{b}_{24}+\cdots =\sum _{k=1}^n{a}_{3k}{b}_{k4} \end{gathered}$$

(2)列的线性组合

我们还是以上面三个矩阵为例，$B$中的每一列就相当于对A中的列进行线性组合得到$C$中的第一列，
我们拿出$B$中的第一列$\left[\begin{array}{c}{b}_{11}\\ b_{21}\\ ⋮\\ b_{n1}\end{array}\right]$ 和 $A$ 进行计算，如下
$$\underset{A}{\left[\begin{array}{ccccc}⋮& ⋮& ⋮& ⋮& ⋮\\ col1& col2& col3& \cdots & \cdots \\ ⋮& ⋮& ⋮& ⋮& ⋮\end{array}\right]}\left[\begin{array}{c}{b}_{11}\\ b_{21}\\ ⋮\\ b_{n1}\end{array}\right]=\left[\begin{array}{c}{c}_{11}\\ c_{21}\\ ⋮\\ c_{m1}\end{array}\right]$$
可以看成
$$b_{11}\left[\begin{array}{c}col1\\ of\\ A\end{array}\right]+b_{21}\left[\begin{array}{c}col2\\ of\\ A\end{array}\right]+\cdots +b_{n1}\left[\begin{array}{c}coln\\ of\\ A\end{array}\right]=\left[\begin{array}{c}{c}_{11}\\ c_{21}\\ ⋮\\ c_{m1}\end{array}\right]$$

(3)行的线性组合

我们拿出$A$中的第一行$\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\end{array}\right]$ 和 $B$ 进行计算，
$$\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\end{array}\right]\underset{B}{\left[\begin{array}{ccc}\cdots & row1& \cdots \\ \cdots & row2& \cdots \\ \cdots & row3& \cdots \end{array}\right]}=\left[\begin{array}{cccc}{c}_{11}& c_{12}& \cdots & c_{1p}\end{array}\right]$$
可以看成
$$a_{11}\left[\begin{array}{c}row1ofB\end{array}\right]+a_{12}\left[\begin{array}{c}row2ofB\end{array}\right]+\cdots +a_{1n}\left[\begin{array}{c}rownofB\end{array}\right]=\left[\begin{array}{cccc}{c}_{11}& c_{12}& \cdots & c_{1p}\end{array}\right]$$

(4)$A$中的列(mx1)X$B$中的行(1xp)

$$AB=\sum _{i=1}^{n}coliofA\ast rowiofB$$
举个例子你就明白了
$$\left[\begin{array}{cc}2& 7\\ 3& 8\\ 4& 9\end{array}\right]\left[\begin{array}{cc}1& 6\\ 0& 0\end{array}\right]=\left[\begin{array}{c}2\\ 3\\ 4\end{array}\right]\left[\begin{array}{cc}1& 6\end{array}\right]+\left[\begin{array}{c}7\\ 8\\ 9\end{array}\right]\left[\begin{array}{cc}0& 0\end{array}\right]=\left[\begin{array}{cc}2& 12\\ 3& 18\\ 4& 24\end{array}\right]$$

(5)分块乘法

$$\left[\begin{array}{cc}{A}_1& A_2\\ A_3& A_4\end{array}\right]\left[\begin{array}{cc}{B}_1& B_2\\ B_3& B_4\end{array}\right]=\left[\begin{array}{cc}{C}_1& C_2\\ C_3& C_4\end{array}\right]$$
$$C_1=A_1{B}_1+A_2{B}_3$$
分块可以不均等分，每一块都要划分相乘应符合乘法原则。

3.矩阵的类型

(1)单位阵 $I$(identity)

$$I={\left[\begin{array}{cccc}1& 0& \cdots & 0\\ 0& 1& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & 1\end{array}\right]}_{n\ast n}$$

(2)转置矩阵(transpose matrix)

定义：$(A^T{)}_{ij}=A_{ji}$
举个例子
$${\left[\begin{array}{cc}1& 3\\ 2& 3\\ 4& 1\end{array}\right]}^T=\left[\begin{array}{ccc}1& 2& 4\\ 3& 3& 1\end{array}\right]$$
自己对比一下你就知道如何求转置矩阵了，然后你可以先看下面的对称矩阵之后反过来继续看这里。
先简单讲讲什么叫方阵，什么叫长方阵。方阵就是长得规规矩矩的，像个正方形的矩阵，如上面的单位阵。而长方阵就是长得像长方形的矩阵，如转置矩阵的例子，两个都是长方阵。好了介绍完这两者区别之后，我就要给出结论了哈哈。
对于所有的长方阵R(对于方阵也是成立的)，$R^{T}R$一定是对称矩阵(symmetric matrix).
先举个例子之后来个证明，我们就拿上面两个矩阵试试不就知道了吗。
$${\left[\begin{array}{cc}1& 3\\ 2& 3\\ 4& 1\end{array}\right]}^T\left[\begin{array}{ccc}1& 2& 4\\ 3& 3& 1\end{array}\right]=\left[\begin{array}{ccc}10& 11& 7\\ 11& 13& 11\\ 7& 11& 17\end{array}\right]$$
证明:$$(R^{T}R{)}^T=R^{T}R$$
可能你对这样的转置不是很明白，那我就细细的讲一遍，举个例子不久明白了么。
假设有两个矩阵$A$和$B$，分别如下
$$A=\left[\begin{array}{ccc}1& 2& 3\\ 3& 3& 1\end{array}\right]B=\left[\begin{array}{ccc}1& 5& 3\\ 2& 6& 4\\ 4& 7& 5\end{array}\right]$$
我们可以先看看
$$AB=\left[\begin{array}{ccc}17& 38& 26\\ 13& 40& 26\end{array}\right](AB{)}^T=\left[\begin{array}{cc}17& 13\\ 38& 40\\ 26& 26\end{array}\right]$$
那让我们看看
$$B^T{A}^T=\left[\begin{array}{ccc}1& 2& 4\\ 5& 6& 7\\ 3& 4& 5\end{array}\right]\left[\begin{array}{cc}1& 3\\ 2& 3\\ 3& 1\end{array}\right]=\left[\begin{array}{cc}17& 13\\ 38& 40\\ 26& 26\end{array}\right]$$
由于我们对$AB$进行转置操作，使得原先的列变成行，而$AB$是B将A中的列进行线性组合，在转置后则要变成$B$将$A$中的行进行线性组合，则$B$要进行左乘同时$A$和$B$都要进行转置才可以。即
$$(AB{)}^T=B^T{A}^T$$

(3)对称矩阵S(symmetric matrix)

定义：$$A^T=A$$
举个例子吧：
$$\left[\begin{array}{ccc}3& 1& 7\\ 1& 2& 9\\ 7& 9& 4\end{array}\right]$$这个就是对称矩阵，对称矩阵很有用，之后还有详解。

(4)置换矩阵$P$(permutation matrix)

置换矩阵是一种系数只由0和1组成的方块矩阵。置换矩阵的每一行和每一列都恰好有一个1，其余元素都是0。上述是维基百科的解释，这个意思是置换矩阵是单位阵$I$各行排列的结果。
举个例子3X3单位阵的置换矩阵有如下：
$${\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]}_{,}{\left[\begin{array}{ccc}0& 1& 0\\ 1& 0& 0\\ 0& 0& 1\end{array}\right]}_{,}{\left[\begin{array}{ccc}0& 0& 1\\ 0& 1& 0\\ 1& 0& 0\end{array}\right]}_{,}{\left[\begin{array}{ccc}1& 0& 0\\ 0& 0& 1\\ 0& 1& 0\end{array}\right]}_{,}{\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 1& 0& 0\end{array}\right]}_{,}\left[\begin{array}{ccc}0& 0& 1\\ 1& 0& 0\\ 0& 1& 0\end{array}\right]$$
总共6种置换矩阵，通过分析，我们可以看成n行（或n列）进行排列而得出的置换矩阵，而这个排列的结果总共是$n!$种。
置换矩阵有一个很好的性质就是$P^{-1}=P^T$，我们可以分析以上例子，随便先找个矩阵比如$\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 1& 0& 0\end{array}\right]$,我们将它和它的转置相乘可得
$$\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 1& 0& 0\end{array}\right]\left[\begin{array}{ccc}0& 0& 1\\ 1& 0& 0\\ 0& 1& 0\end{array}\right]=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$$
我们惊奇地发现它和它的转置相乘变成了单位阵即$P{P}^T=I$，根据矩阵的逆的定义（这里不懂的可以先跳过）我们可以得到$P^{-1}=P^T$，你也可以试试其他的置换矩阵。为什么呢，等到我讲到正交矩阵的时候你在回来看你就明白了。