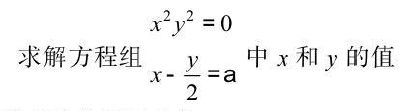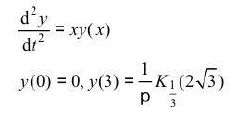matlab---方程求解

代数方程符号解

>> syms a b c x
>> s = a * x ^ 2 + b * x + c;
>> solve(s)

ans =

 -(b + (b^2 - 4*a*c)^(1/2))/(2*a)
 -(b - (b^2 - 4*a*c)^(1/2))/(2*a)

%如果想求指定符号解，将其加入solve中
>> b = solve(s, b)

b =

-(a*x^2 + c)/x

代数方程组中符号解

>> syms x y alpha
>> [x, y] = solve(x^2*y^2, x-y/2-alpha)

x =

 alpha
     0


y =

        0
 -2*alpha

>> s = solve('u^2-v^2=a^2', 'u+v=1', 'a^2-2*a=3');
>> m = [s.a, s.u, s.v]

m =

[ -1, 1,  0]   %每一行包含了方程组的一组解
[  3, 5, -4]

齐次方程组求解
齐次线性方程AX=0, rank(A)=r

>> a = [1 1 1 1 -3 -1 1;
        1 0 0 0 1 1 0;
        -2 0 0 -1 0 -1 -2];
>> r = rank(a);
>> x = null(a, 'r')            %注意r必须加引号

x =                            %列向量为ax=0的一个基本解

     0    -1    -1     0
    -1     2     1     1
     1     0     0     0
     0     2     1    -2
     0     1     0     0
     0     0     1     0
     0     0     0     1

非齐次方程组求解
rank(a) = r = n

>> a = [5 0 4 2; 1 -1 2 1; 4 1 2 0; 1 1 1 1];
>> b = [3; 1; 1; 0];
>> x = zeros(4, 1);     %4元列向量
>> x = linsolve(a, b)

x =

    1.0000
   -1.0000
   -1.0000
    1.0000

rank(a) = r > n

>> a = [2 -1 3;3 1 -5;4 -1 1;1 3 -13];
>> b = [3; 0; 3; -6];
>> x = a\b

x =

    1.0000
    2.0000
    1.0000

微分方程求解

>> dsolve('Dy = t * y')

ans =

C2*exp(t^2/2)

%也可加入初始条件
>> x = dsolve('Dy = t * y', 'y(0) = 2')

x =

2*exp(t^2/2)

微分方程组求解

>> y = dsolve('D2y=x*y', 'y(0)=0', 'y(3)=besselk(1/3, 2*sqrt(3))/pi', 'x')

y =

(3^(1/2)*besselk(1/3, 2*3^(1/2))*airy(0, x))/(pi*(3^(1/2)*airy(0, 3) - airy(2, 3))) - (besselk(1/3, 2*3^(1/2))*airy(2, x))/(pi*(3^(1/2)*airy(0, 3) - airy(2, 3)))

求导

>> syms x;
>> y = sin(5 * x);
>> diff(y)        %一阶导

ans =

5*cos(5*x)

 >> diff(y, 2)    %二阶导

ans =

-25*sin(5*x)

>> syms s t
>> f = sin(s * t);
>> diff(f, t)     %对t求导

ans =

s*cos(s*t)

求积分

>> syms x t z alpha
>> int(-2 * x / (1 + x^2) ^ 2)     %积分

ans =

1/(x^2 + 1)

>> int(x * log(1 + x), 0 , 1)      %定积分

ans =

1/4

>> int(2 * x, sin(t), 1)          %定积分，积分范围为（sin(t), 1)

ans =

cos(t)^2

求极限

>> syms h n x;
>> limit( (cos(x+h) - cos(x) ) / h, h, 0)  %当h趋向于0时的极限

ans =

-sin(x)

>> limit(x/abs(x), x, 0, 'left')    %左极限

ans =

-1

>> limit(x/abs(x), x, 0, 'right')   %右极限

ans =

1

求级数

>> syms k;
>> symsum(1/2^k, 1, inf)    %1到无穷的和

ans =

1

>> symsum(sin(k*pi)*k, 0, n)   %0到n的和

ans =

- (exp(-pi*(n + 1)*i)*(2*n + 1)*i)/8 + (exp(pi*(n + 1)*i)*(2*n + 1)*i)/8

>> symsum(x^k/sym('k!'), k, 0, inf)  %自变量为k，0到无穷的和

ans =

exp(x)