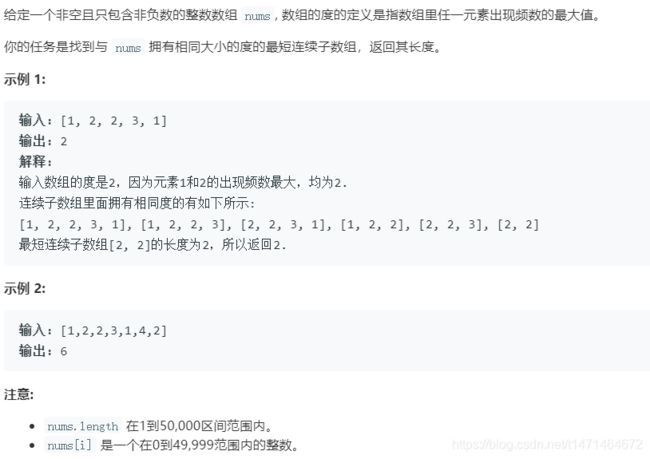
5.23力扣 最大子数组和 前缀和+单调栈
面试题 16.16. 部分排序
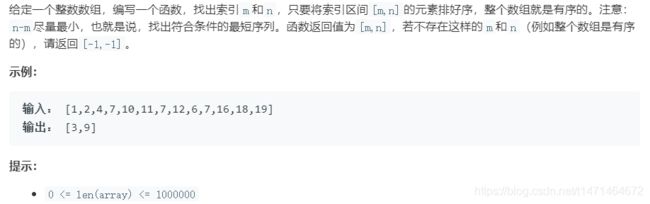
当一个数a[i]左侧有一个数比它大的时候,或者右侧有一个数比它小的时候,它一定是在被排序的序列内。
因为一个数如果 左边的数都比它小,右边的数都比它大,显然没必要排序。
那么对于元素 a[i] 来说,如果它左边存在大于 a[i] 的元素,那么 a[i] 是一定要参与到排序里去的。或者说如果它右边存在小于 a[i] 的元素,那么 a[i] 也是要参与到排序里去的。
所以我们只需要寻找最靠右的那个数(满足左边存在大于它的数),和最靠左的那个数(满足右边存在小于它的数),那么这两个数之间就是要排序的区间了。
为什么最靠右的那个(满足左边存在大于它的数)数一定能保证右边没有更小的数了呢?因为如果右边还有更小的数,那么那个更小的数才是更靠右的啊,这就矛盾了。
class Solution:
def subSort(self, array: List[int]) -> List[int]:
#分成三部分,左侧排好序,中间未排序,右侧排好序
#left部分最大值应小于中间部分最小值,right部分最小值应大于中间部分最大值,如果不符合,则更新中间部分左右边界
#对于a[i],如果左边存在比他大的值,说明a[i]需要排序,找到最右边的a[i]
#对于a[j],如果右边存在比他小的值,说明a[j]需要排序,找到最左边的a[j],此时l左边的值
maxn,minn=float('-inf'),float('inf')
l,r=-1,-1
for i in range(len(array)):
if array[i]<maxn:
r=i
else:
maxn=array[i]
for j in range(len(array)-1,-1,-1):
if array[j]>minn:
l=j
else:
minn=array[j]
return [l,r]
class Solution:
def findShortestSubArray(self, nums: List[int]) -> int:
arr=defaultdict(int)
for i in nums:
arr[i]+=1
minl=float('inf')
b=max(arr.values())
l=0
hash=defaultdict(int)
for r in range(len(nums)):
hash[nums[r]]+=1
while max(hash.values())== b and l<=r:
minl=min(minl,r-l+1)
hash[nums[l]]-=1
l+=1
return minl
672. 灯泡开关 Ⅱ
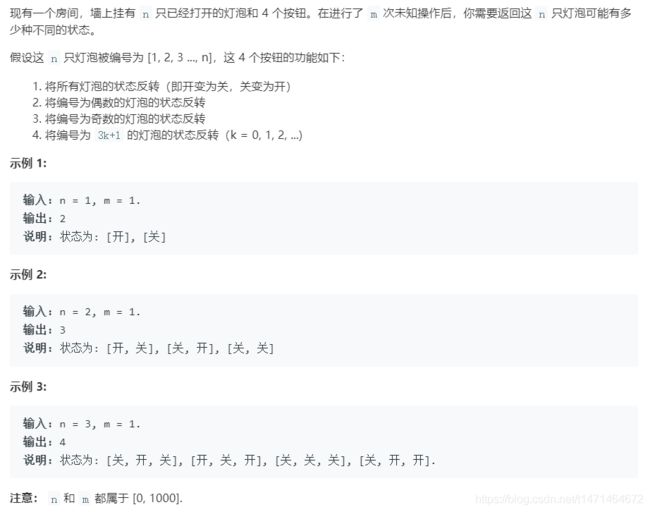
题解:
https://blog.csdn.net/lemonmillie/article/details/86619755
进行第一种操作时,一个灯泡和n个灯泡是一样的,只有开关关闭两种状态,
进行第二种、第三种操作,只有两个灯泡和n个灯泡是一样的,奇数看成一个灯泡,偶数看成一个灯泡。
进行第四种操作时,只有3个灯泡和有n个灯泡是一样的,3k、3k + 1、3k + 2看成三个灯泡。
n=min(n,3)
如果n >= 3,m >= 3,则可能情况就是3个灯泡的所有可能情况,每个灯泡2种情况,则总数是2**3=8种
class Solution(object):
def flipLights(self, n, m):
"""
:type n: int
:type m: int
:rtype: int
"""
if n==0:
return 0
if m==0:
return 1
if n==1:
return 2
if n==2:
return 3 if m==1 else 4
if m==1:
return 4
if m==2:
return 7
return 8
前缀和+单调栈
560 1248 1371 前缀和+哈希表
1310. 子数组异或查询
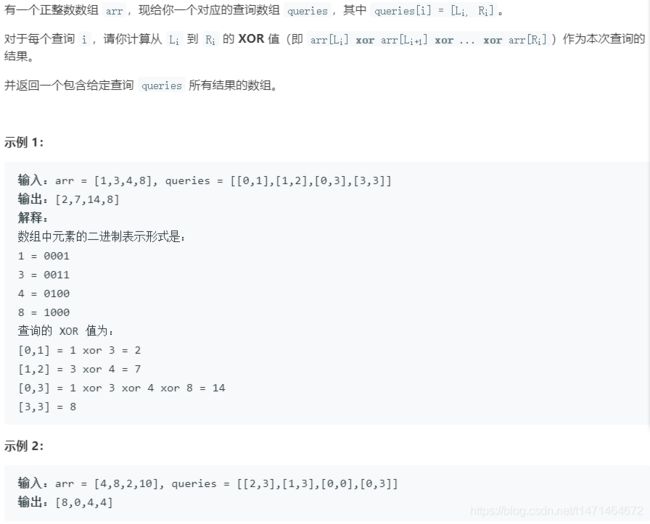

异或的性质:x ^ y ^ x = y
0^x=x
nums :1 3 4 8
pre : 0 ,0^1 0^1^3 0^1^3^4 0^1^3^4^8
nums[1]^nums[3]=pre[1]^pre[4]
class Solution:
def xorQueries(self, arr: List[int], queries: List[List[int]]) -> List[int]:
pre=[0]
res=[]
for i in range(len(arr)):
pre.append(pre[i]^arr[i])
for l,r in queries:
res.append(pre[l]^pre[r+1])
return res
class NumArray:
def __init__(self, nums: List[int]):
self.pre=[0]*(len(nums)+1)
for i in range(1,len(nums)+1):
self.pre[i]=self.pre[i-1]+nums[i-1]
def sumRange(self, i: int, j: int) -> int:
return self.pre[j+1]-self.pre[i]
单调栈
参考:https://muyids.github.io/simple-algorithm/chapter/%E5%8D%95%E8%B0%83%E6%A0%88.html
单调栈分两类问题:
一种是从中间某一元素开始,求解此元素左右两边的最大或最小值 另一种求解整个序列,递增或递减子序列的最大跨度
单调递增栈用于查找两边第一个小于当前元素的值,单调递减栈用于查找两边第一个大于当前元素的值
85 最大矩形 同84
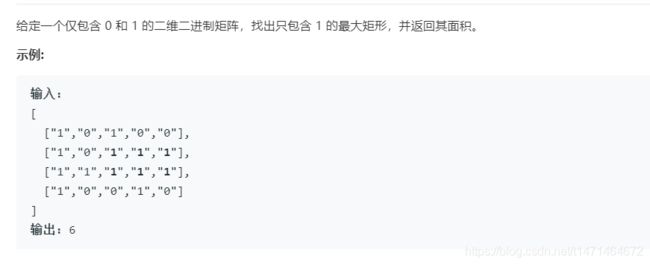
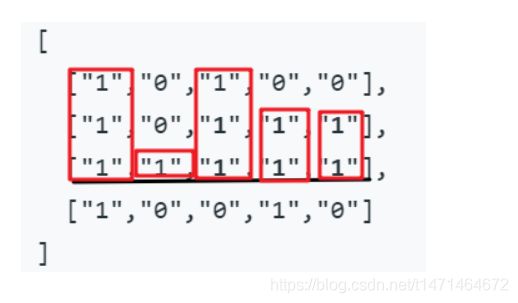
以当前行为底,每一层计算一次高度,求构成的最大矩形面积
为了保证可以弹出所有数据,高度数组前后增加0
class Solution:
def maximalRectangle(self, matrix: List[List[str]]) -> int:
if not matrix or not matrix[0]:
return 0
row=len(matrix)
col=len(matrix[0])
#两端增加哨兵元素
#最后一个0是为了保证计算最后面的高度单调非递减的矩形面积,需要一个0将栈顶元素弹出,最后留在栈内的元素都是高度为0的列
heights=[0]*(col+2)
res=0
for i in range(row):
stack=[0]
for j in range(1,col+2):
#遍历每一列计算当前行时的矩形高度,如果为‘0’,则高度清0
#先计算高度,在判断是否需要更新面积
if 1<=j<=col:
if matrix[i][j-1]=='1':
heights[j]+=1
else:
heights[j]=0
#构造单调非递减栈,当前高度小于栈顶高度时,弹出栈顶元素cur,以cur为高度,新的栈顶元素为左边最近的小于cur高度的矩形,当前元素heights[j]为右边最近的小于cur高度的,宽*高
while stack and heights[stack[-1]]>heights[j]:
cur=stack.pop()
res=max(res,(j-stack[-1]-1)*heights[cur])
stack.append(j)
return res
全局单调栈 962 1124
1124. 表现良好的最长时间段 外层循环中,如果i 用单调栈构造单调递减栈,存储前缀和数组中最小元素的最左边下标,然后从后往前遍历,当pre[j]大于栈顶所指元素时,更新宽度 962. 最大宽度坡 1186 删除一次得到子数组的最大值 动态规划法: 53. 最大子序和
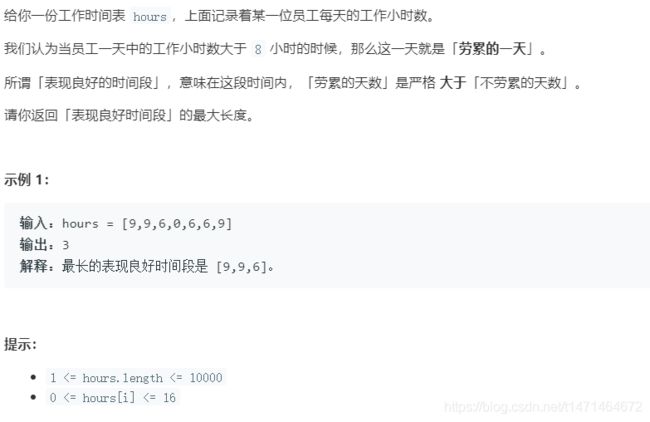
将大于8h的设为1,小于8h的设为-1,变成了求某一个子列的和大于0,且这个子列最长
用前缀和可以很快的计算出任何一段子列的和
返回表现良好时间段的最大长度,即求最长的一段中,得分 1 的个数大于得分 −1 的个数,也就是求 score 数组中最长的一段子数组,其和大于 0,
目的是找到一个 i
在内层循环中,那么对于ires = 0
num = len(pre)
for i in range(num):
for j in range(num - 1, i, -1):
if pre[i] < pre[j]:
res = max(j - i, res)
continue # 说明此时剩下的(i,j)不是候选项,从新的i继续
因为如果pre[j] > pre[i1], 那么(i1, j)一定不会是答案,因为(i, j)更长.
如果pre[j] < pre[i1], 那么(i1, j)也一定不会是答案,因为我们要找pre[j] -pre[i1] > 0的(i, j)
所以从头遍历pre,找到一个严格单调递减的数组
从单调递减栈从选取i,pre从右往左遍历j
因为j从后往前遍历,当满足条件时,用(stack[-1],j)更新宽度,此时j的左边不用再遍历了,因为就算符合条件,宽度也没有(stack[-1],j)大,同时j的右边数据都小于栈顶所指元素,且单调递减栈,栈的左边元素数值都大于栈顶元素,那么也不需要从pre的右端重新遍历,因为j右边的pre都不满足pre[j]>pre[i],所以更新完宽度弹出栈顶元素,继续判断class Solution:
def longestWPI(self, hours: List[int]) -> int:
arr=[]
for i in range(len(hours)):
if hours[i]>8:
arr.append(1)
else:
arr.append(-1)
pre=[0]*(len(arr)+1)
for i in range(1,len(arr)+1):
pre[i]=pre[i-1]+arr[i-1]
stack=[]
res=0
# 顺序生成单调栈,栈中元素从第一个元素开始严格单调递减,最后一个元素肯定是数组中的最小元素所在位置
#保存从左到右出现的最小值的最左边下标
for i in range(len(pre)):
while not stack or pre[stack[-1]]>pre[i]:
stack.append(i)
for i in range(len(pre)-1,-1,-1):
while stack and pre[stack[-1]]<pre[i]:
res=max(res,i-stack[-1])
stack.pop()
return res

根据题意需要找出最大宽度并且A[i] <= A[j],很容易想到i需要从左往右,j从右往左遍历数组。
A[i]的值越小越容易得到最大宽度,同时还要考虑i尽可能的小
正向扫描记录严格的单调递减A[i]的下标,反向扫描比较A[j]与栈顶元素,符合条件则弹出栈顶元素,更新坡度最大子数组和

前后缀和:
l[i]表示从左边开始的以arr[i]结尾的子数组和的最大值
r[i]表示从右边开始的以arr[i]结尾的子数组和的最大值
l[i - 1] + r[i + 1]的含义就是删除arr[i]的子数组最大值class Solution:
def maximumSum(self, arr: List[int]) -> int:
if len(arr)==1:
return arr[0]
#l表示从左边开始,以arr[i]为结尾的subArraySum的最大值
#r表示从右边开始,以arr[i]为结尾的subArraySum的最大值
l=[arr[0]]*len(arr)
r=[arr[-1]]*len(arr)
res=float('-inf')
for i in range(1,len(arr)):
l[i]=max(arr[i],l[i-1]+arr[i])
res=max(res,l[i])
for i in range(len(arr)-2,-1,-1):
r[i]=max(arr[i],r[i+1]+arr[i])
res=max(res,r[i])
for i in range(1,len(arr)-1):
res=max(res,l[i-1]+r[i+1])
return res
dp[i][j]表示以arr[i]结尾的,已经删除j次的子数组最大值
dp[i][0]:表示以arr[i]结尾的,最大子数组和(以防有负数,要和当前值比较)(前缀和)class Solution:
def maximumSum(self, arr: List[int]) -> int:
if len(arr)==1:
return arr[0]
k=1
#dp[i][j]表示以arr[i]为结尾,删除J次的子数组和最大值
dp=[[0 for _ in range(k+1)] for _ in range(len(arr))]
dp[0][0]=arr[0]
maxr=float('-inf')
for i in range(1,len(arr)):
#以arr[i]为结尾的,最大子数组和
dp[i][0]=max(dp[i-1][0]+arr[i],arr[i])
#因为可以删除也可不删除,
maxr=max(maxr,dp[i][0])
for i in range(1,len(arr)):
for j in range(1,k+1):
#删除arr[i]元素 或者不删
dp[i][j]=max(dp[i-1][j-1],dp[i-1][j]+arr[i])
maxr=max(maxr,dp[i][j])
return maxr
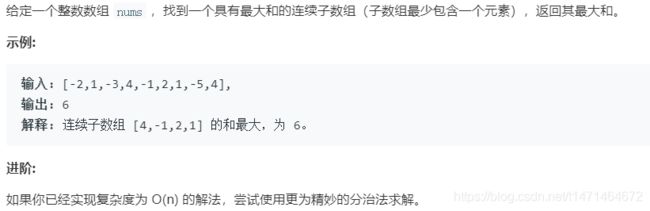
动态规划:
nums[i]是单独成为一段还是加入上一段
dp[i]只与dp[i-1]有关,可以考虑用一个变量维持,空间复杂度降到O(1)class Solution:
def maxSubArray(self, nums: List[int]) -> int:
if len(nums)==1:
return nums[0]
# dp=[0]*len(nums)
maxr=nums[0]
# dp[0]=nums[0]
pre=nums[0]
for i in range(1,len(nums)):
pre=max(pre+nums[i],nums[i])
maxr=max(maxr,pre)
# dp[i]=max(dp[i-1]+nums[i],nums[i])
# maxr=max(maxr,dp[i])
return maxr