[bzoj5016][莫队算法]一个简单的询问

Description

给你一个长度为N的序列ai，1≤i≤N和q组询问，每组询问读入l1,r1,l2,r2，需输出
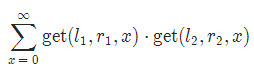
get(l,r,x)表示计算区间[l,r]中，数字x出现了多少次。

Input

第一行，一个数字N，表示序列长度。 第二行，N个数字，表示a1～aN 第三行，一个数字Q，表示询问个数。
第4～Q+3行，每行四个数字l1,r1,l2,r2，表示询问。 N,Q≤50000 N1≤ai≤N 1≤l1≤r1≤N 1≤l2≤r2≤N
注意：答案有可能超过int的最大值

Output

对于每组询问，输出一行一个数字，表示答案

Sample Input

5

1 1 1 1 1

2

1 2 3 4

1 1 4 4

Sample Output

4

1

题解

这个一眼可以看出来莫队吧。。
然后一开始打了个非常不优秀的双区间莫队，T成傻子
怎么办？？
我们把式子推一下，可以化成
(Sigma(get(0,r1,x))−Sigma(get(0,l1−1,x)))∗(Sigma(get(0,r2,x)−Sigma(get(0,l2−1,x)))) ( S i g m a ( g e t ( 0 , r 1 , x ) ) − S i g m a ( g e t ( 0 , l 1 − 1 , x ) ) ) ∗ ( S i g m a ( g e t ( 0 , r 2 , x ) − S i g m a ( g e t ( 0 , l 2 − 1 , x ) ) ) )
= Sigma(get(0,r1,x))∗Sigma(get(0,r2,x))−Sigma(get(0,r1,x))∗Sigma(get(0,l2−1,x))−Sigma(get(0,l1−1,x))∗Sigma(0,r2,x)+Sigma(get(0,l1−1,x))∗Sigma(get(0,l2−1,x)) S i g m a ( g e t ( 0 , r 1 , x ) ) ∗ S i g m a ( g e t ( 0 , r 2 , x ) ) − S i g m a ( g e t ( 0 , r 1 , x ) ) ∗ S i g m a ( g e t ( 0 , l 2 − 1 , x ) ) − S i g m a ( g e t ( 0 , l 1 − 1 , x ) ) ∗ S i g m a ( 0 , r 2 , x ) + S i g m a ( g e t ( 0 , l 1 − 1 , x ) ) ∗ S i g m a ( g e t ( 0 , l 2 − 1 , x ) )
设 G(x,y,c) G ( x , y , c ) 表示 Sigma(get(0,x,c))∗Sigma(get(0,y,c)) S i g m a ( g e t ( 0 , x , c ) ) ∗ S i g m a ( g e t ( 0 , y , c ) )
那么还可以化为
G(r1,r2,x)−G(r1,l2−1,x)−G(l1−1,r2,x)+G(l1−1,l2−1,x) G ( r 1 , r 2 , x ) − G ( r 1 , l 2 − 1 , x ) − G ( l 1 − 1 , r 2 , x ) + G ( l 1 − 1 , l 2 − 1 , x )
于是我们可以把一个式子拆成四个，分别莫队算贡献
然后就没了。。

#include
#include
#include
#include
#include
using namespace std;
typedef long long LL;
struct node
{
    int l,r,pos,op;
}a[211000];int cnt,n,q;
int pos[51000],block;
bool cmp(node n1,node n2){return pos[n1.l]!=pos[n2.l]?pos[n1.l]<pos[n2.l]:n1.rint col[51000];
int gx[51000],gy[51000];
LL ans;
LL answer[51000];
void addl(int now){gx[col[now]]++;ans+=gy[col[now]];}
void addr(int now){gy[col[now]]++;ans+=gx[col[now]];}
void dell(int now){gx[col[now]]--;ans-=gy[col[now]];}
void delr(int now){gy[col[now]]--;ans-=gx[col[now]];}

int main()
{
    scanf("%d",&n);block=sqrt(n);
    for(int i=1;i<=n;i++)scanf("%d",&col[i]),pos[i]=(i-1)/block+1;
    scanf("%d",&q);
    for(int i=1;i<=q;i++)
    {
        int l1,r1,l2,r2;
        scanf("%d%d%d%d",&l1,&r1,&l2,&r2);
        cnt++;a[cnt].l=r1;a[cnt].r=r2;a[cnt].pos=i;a[cnt].op=1;
        cnt++;a[cnt].l=r1;a[cnt].r=l2-1;a[cnt].pos=i;a[cnt].op=-1;
        cnt++;a[cnt].l=l1-1;a[cnt].r=r2;a[cnt].pos=i;a[cnt].op=-1;
        cnt++;a[cnt].l=l1-1;a[cnt].r=l2-1;a[cnt].pos=i;a[cnt].op=1;
    }
    sort(a+1,a+1+cnt,cmp);
    for(int i=1;i<=a[1].l;i++)gx[col[i]]++;
    for(int i=1;i<=a[1].r;i++)gy[col[i]]++;
    for(int i=1;i<=n;i++)ans+=(LL)gx[i]*gy[i];
    answer[a[1].pos]+=ans*a[1].op;
    int l=a[1].l,r=a[1].r;
    for(int i=2;i<=cnt;i++)
    {
        while(lwhile(l>a[i].l)dell(l--);
        while(rwhile(r>a[i].r)delr(r--);
        answer[a[i].pos]+=ans*a[i].op;
    }
    for(int i=1;i<=q;i++)printf("%lld\n",answer[i]);
    return 0;
}