零钱兑换--动态规划
Leetcode 323
零钱兑换
题目描述:给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
示例1:
输入: coins = [1, 2, 5], amount = 11
输出: 3
解释: 11 = 5 + 5 + 1
示例2:
输入: coins = [2], amount = 3
输出: -1
解法一:穷举法
解题思路: 每一种硬币种类的组合都求出来,当它满足和等于amount且数量较小时,就用一个MinCost来保存
代码实现:这里代码只能用递归来写,因为你不知道有多少种硬币
public class Solution {
public int coinChange(int[] coins, int amount)
{
return coinChange(0, coins, amount);
}
private int coinChange(int idxCoin, int[] coins, int amount)
{
if (amount == 0)
return 0;
if (idxCoin < coins.length && amount > 0)
{
int maxVal = amount / coins[idxCoin];
int minCost = Integer.MAX_VALUE;
for (int x = 0; x <= maxVal; x++)
{
if (amount >= x * coins[idxCoin])
{
int res = coinChange(idxCoin + 1, coins, amount - x * coins[idxCoin]);
if (res != -1)
minCost = Math.min(minCost, res + x);//从低往上传的minCost+x跟当前的minCost比较
}
}
return minCost == Integer.MAX_VALUE? -1: minCost;
}
return -1;
}
}
时间复杂度O(S^n),可能每种可能都要试一遍
时间复杂度O(n),最坏的情况下,递归的最大深度为n
这个解法显然超时了
解法二:动态规划(自上往下)
解题思路:
F(S): 组成金额S所需的最少硬币数量
[c0,c1,c2,c2…]:每枚硬币的面额
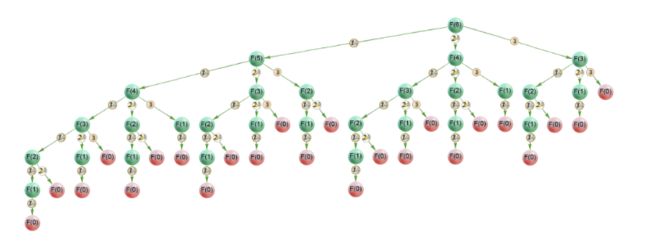
这个问题其实是有最优子结构的,我们假设F©是组成金额所需的最少硬币,则最后一枚硬币可能有好几种可能,所以F(C) = F(C-c)+1
我们可以看到,这里就是我们熟悉的动态规划题了,我们知道,动态规划的一个重要思想就是减少重复计算,这里我们可以看到f(1)被计算了11次,我们应该把每次计算的F(i)值保存下来
完整代码
public class Solution {
public int coinChange(int[] coins, int amount)
{
return coinChange(coins, amount, new int[amount]);
}
private int coinChange(int[] coins, int rem, int[] count)
{
if(rem<0)
return -1;
if(rem==0)
return 0;
if(count[rem-1]!=0) //计算过的,直接返回
return count[rem-1];
int min = Integer.MAX_VALUE;
for(int coin: coins)
{
int res = coinChange(coins,rem-coin,count);
if(res>=0 && res时间复杂度为O(Sn)
空间复杂度为O(S)
解法三:动态规划(自下往上)
**解题思路:**跟上面的方法类似,但是这次是从下往上求,可以得到转移方程为:
F(i) = min(F(i-c1),F(i-c2),...,F(i-ci))+1
完整代码:
public class Solution {
public int coinChange(int[] coins, int amount)
{
int max = amount+1;
int[] dp = new int[amount+1];
Arrays.fill(dp, max); //初始化为最大
dp[0] = 0;
for(int i=1; i<=amount; i++) //求F(1)到F(amount)
{
for(int j=0; jamount?-1:dp[amount];
}
}
时间复杂度为O(Sn)
空间复杂度为O(S)
解法四:DFS+剪枝
解题思路:
我们从面额大的硬币开始减。从使用最多枚递减到0枚,然后有两种情况要退出递归
-
当我们使用当前硬币恰好能凑出amount,则退出递归,因为再往下减也不会更好
-
当我们当前使用的硬币数量+1>=之前求出的最少硬币数量,也要退出递归,因为你减少一个当前使用的硬币,用来兑换更小面额的硬币,情况不会更好
class Solution { int ans=Integer.MAX_VALUE; public int coinChange(int[] coins, int amount) { Arrays.sort(coins); dfs(coins,coins.length-1,amount,0); return ans==Integer.MAX_VALUE?-1:ans; } public void dfs(int[] coins,int index,int amount,int cnt){ if(index<0){ return; } for(int c=amount/coins[index];c>=0;c--){ int na=amount-c*coins[index]; int ncnt=cnt+c; if(na==0){ ans=Math.min(ans,ncnt); break;//剪枝1 } if(ncnt+1>=ans){ //这个ans是从下面递归求出来的 break; //剪枝2 } dfs(coins,index-1,na,ncnt); } } }
心得体会
一味的做题反而不好,而且我连最开始的组合怎么写都忘了,当时竟然每想到递归,一看到动态规划题目 ,就总想着上面扩展,转移方程,结果连最基本的递归都忘了,而且动态规划的关键也不是找出什么转移方程,主要还是减少重复的计算
解题思路以及题目来源
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/coin-change/solution/322-ling-qian-dui-huan-by-leetcode-solution/
来源:力扣(LeetCode)
是找出什么转移方程,主要还是减少重复的计算
解题思路以及题目来源
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/coin-change/solution/322-ling-qian-dui-huan-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。