6.11 力扣 一开始不想做题效率就下来了 回溯法(全排列问题)
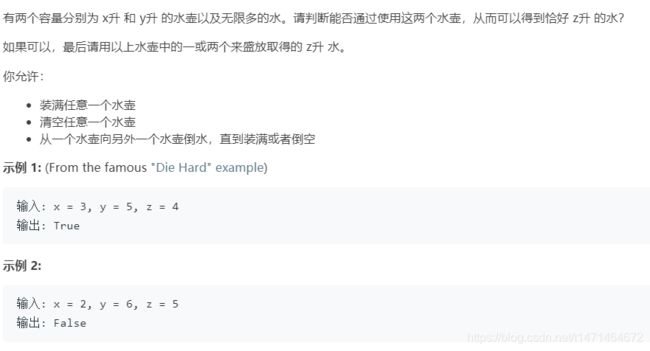
365. 水壶问题
数学方法:
每次操作只会让桶里的水总量增加 x,增加 y,减少 x,或者减少 y,两个桶不可能同时有水且不满。操作的结果都至少有一个桶是空的或者满的;
我们可以认为每次操作只会给水的总量带来 x 或者 y 的变化量。两个壶中水的总量一定为:ax+by,a,b是整数,因此我们的目标可以改写成:找到一对整数 a,b,使得 ax+by==z,且z<=x+y
贝祖定理:若x,y是整数,且gcd(x,y)=d,那么对于任意的整数a,b,ax+by都一定是d的倍数,特别地,一定存在整数a,b,使ax+by=d成立。因此我们只需要找到 x, y 的最大公约数并判断 z 是否是它的倍数即可
class Solution:
def canMeasureWater(self, x: int, y: int, z: int) -> bool:
if x+y<z:
return False
if x==0 or y==0:
return z==0 or x+y==z
return z%math.gcd(x,y)==0
891. 子序列宽度之和

子序列,不要求连续,因此可以先排序在计算

(2**(left)-2**(right))*A[i]
对于索引为i的元素,左边有 i个元素,右边有n-i-1个元素

class Solution:
def sumSubseqWidths(self, A: List[int]) -> int:
mod=1000000007
A.sort()
two=[0]*len(A)
two[0]=1
ans=0
#提前计算2的幂
for i in range(1,len(A)):
two[i]=two[i-1]<<1
for i in range(len(A)):
left=i
right=len(A)-i-1
ans+=((two[left]-two[right])*A[i])
return ans%mod
面试题 16.21. 交换和

s1=sum(arr1),s2=sum(arr2)
s1-a+b=s2-b+a
a-b=(s1-s2)/2
如果s1-s2为奇数,那么不存在可以交换的数据
class Solution:
def findSwapValues(self, array1: List[int], array2: List[int]) -> List[int]:
s1=sum(array1)
s2=sum(array2)
#用List会超时,set可以
a1=set(array1)
target=(s1-s2)/2
if (s1-s2)&1:
return []
for b in array2:
if b+target in a1:
return [int(b+target),b]
return []
1442. 形成两个异或相等数组的三元组数目


如果ab,则a^b0
找到一个区间i-k,使中间数据异或值为0,固定了两端索引,中间的j随便取,j取任意满足i
class Solution:
def countTriplets(self, arr: List[int]) -> int:
if len(arr)<2:
return 0
res=0
for i in range(len(arr)):
tmp=arr[i]
for j in range(i+1,len(arr)):
tmp^=arr[j]
if tmp==0:
res+=j-i
return res
利用前缀异或结果 60. 第k个排列 回溯加剪枝 31. 下一个排列 9. 回文数 面试题 17.19. 消失的两个数字

故可以定义一个 xor[i]=a[0] ^ a[1]^ …^ a[i]
只要求得满足 xor[i-1]==xor[k] 的i,k 即可满足①式。
找到两个相同前缀异或值的下标i,k,(i+1)-k即满足条件,满足i+1class Solution:
def countTriplets(self, arr: List[int]) -> int:
if len(arr)<2:
return 0
res=0
# 存储前缀异或结果相同的下标
dic={0:[-1]}
tmp=0
for i in range(len(arr)):
tmp^=arr[i]
if tmp not in dic:
dic[tmp]=[i]
else:
for j in dic[tmp]:
res+=i-j-1
dic[tmp].append(i)
return res

math.factorial; 阶乘 函数
根据每一位数字,确定第k个排列
https://leetcode-cn.com/problems/permutation-sequence/solution/golang-100-faster-by-a-bai-152/


排列的编号为从 0 到 N! - 1,而不是从 1到 N!。因此 N = 3 时,k = 2。k=k-1class Solution:
def getPermutation(self, n: int, k: int) -> str:
ans=[str(i) for i in range(1,n+1)]
#索引从0开始,第k个的索引为k-1,所以要减去1
k-=1
res=''
while n>0:
n-=1
#除数,余数
a,k=divmod(k,math.factorial(n))
res+=ans.pop(a)
return res
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
res=[]
def dfs(arr,tmp):
if len(arr)==0:
res.append(tmp)
for i in range(len(arr)):
dfs(arr[:i]+arr[i+1:],tmp+[arr[i]])
dfs(nums,[])
return res
class Solution:
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
res=[]
def dfs(arr,tmp):
if len(arr)==0:
if tmp not in res:
res.append(tmp)
for i in range(len(arr)):
dfs(arr[:i]+arr[i+1:],tmp+[arr[i]])
dfs(nums,[])
return res
在一定会产生重复结果集的地方剪枝。可以在搜索之前就对候选数组排序,一旦发现这一支搜索下去可能搜索到重复的元素就停止搜索,这样结果集中不会包含重复元素。
1)用过的元素不能再被使用
2)当当前元素和前一个元素值相同(此处隐含这个元素的index>0),并且前一个元素还没有被使用过的时候,我们要剪枝
如果前一个重复元素没有使用过,那么在当前重复元素下一层的可选项中一定会存在,存在 2,2’ 和2’ 2一致的情况,需要剪枝class Solution:
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
nums.sort()
res=[]
used=[False]*len(nums)
def dfs(arr,used,tmp):
if len(tmp)==len(arr):
res.append(tmp)
return
for i in range(len(arr)):
if used[i]:
continue
if i>0 and nums[i]==nums[i-1] and not used[i-1]:
continue
used[i]=True
dfs(arr,used,tmp+[arr[i]])
used[i]=False
dfs(nums,used,[])
return res

需要从右边找到第一对两个连续的数字 a[i] 和 a[i-1],它们满足 a[i]>a[i-1],现在,没有对 a[i-1]右侧的重新排列可以创建更大的排列,因为该子数组由数字按降序组成。因此,我们需要重新排列 a[i-1]右边的数字,包括它自己。
需要倒序从后面的数寻找比该索引值第一个大的数的索引。
为了使增幅尽可能的小,在尽可能靠右的低位进行交换,需要从后向前查找,将一个尽可能小的大数与前面的小数(索引为i-1)交换,将「大数」换到前面后,当前I-1处的值已经变成大数了,交换并不改变i-1后面的数的降序排列,需要将i-1后面的所有数重置为升序,升序排列就是最小的排列。以 123465 为例:首先按照上一步,交换 5 和 4,得到 123564;然后需要将 5 之后的数重置为升序,得到 123546。显然 123546 比 123564 更小,123546 就是 123465 的下一个排列
字典序是从开始挨个数字进行比较,class Solution:
def nextPermutation(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
for i in range(len(nums)-1,-1,-1):
if nums[i]>nums[i-1]:
#从i开始到结尾的数组是降序排列,已经不能再大了,所以要改变i-1位的值,换成较小的大数,所以从最后一位开始,找到的第一个大于Nums[i-1]的数,就是i-1后面的数中第一个大于该索引值的数
for j in range(len(nums)-1,i-1,-1):
if nums[j]>nums[i-1]:
nums[i-1],nums[j]=nums[j],nums[i-1]
#交换之后需要对i-1后面数由降序变为升序
nums[i:]=sorted(nums[i:])
return

将后半段数字取出来反转,用%10取出最后一位数字,每取一位最低数字后,都要自除以10

末尾为0的数直接返回False,因为整形的数首位不可能为0class Solution:
def isPalindrome(self, x: int) -> bool:
if x<0 or x%10==0 and x!=0:
return False
res=0
while x>res:
y=x%10
res=res*10+y
x//=10
return x==res or x==res//10
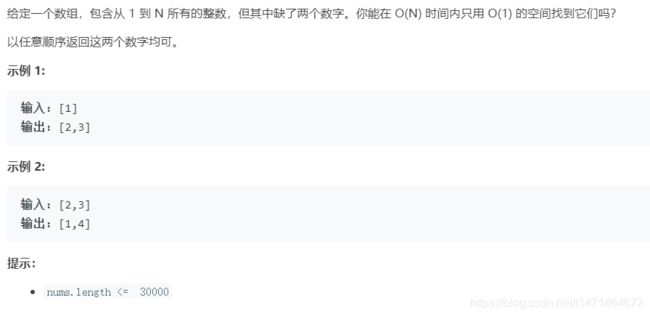
根据异或值
按照 ans 某一位为 1 来划分两个集合,ans为1的一位说明两个数字在这一位上是不同的,其实取任意一位是 1 的位都是可以的。但是最简单的方法就是取最低位 1 ,因为这样可以采用位运算 x&(−x) 直接得到
x&(-x):返回二进制最右边的1class Solution:
def missingTwo(self, nums: List[int]) -> List[int]:
ans=0
n=len(nums)
for num in nums:
ans^=num
for i in range(1,n+3):
ans^=i
#根据某一位为1划分两个集合,每个集合包含一个消失的数字
ans=ans&(-ans)
a_a=0
a_b=0
for num in nums:
if num&ans:
a_a^=num
else:
a_b^=num
for i in range(1,n+3):
if i&ans:
a_a^=i
else:
a_b^=i
return [a_a,a_b]

