【算法】动态规划+“背包九讲”原理超详细讲解+常见dp问题（9种）总结

一.动态规划（DP）

动态规划（DP）通俗讲解
1、什么是动态规划？
这里参考百度百科，动态规划是求解决策过程最优化的数学方法。把多阶段过程转化为一系列单阶段问题，利用各阶段之间的关系，逐个求解，创立了解决这类过程优化问题的新方法——动态规划。

2、什么时候要用动态规划？
如果要求一个问题的最优解（通常是最大值或者最小值），而且该问题能够分解成若干个子问题，并且小问题之间也存在重叠的子问题，则考虑采用动态规划。

3、怎么使用动态规划？
我把下面称为动态规划五部曲：

1. 判题题意是否为找出一个问题的最优解
2. 从上往下分析问题，大问题可以分解为子问题，子问题中还有更小的子问题
3. 从下往上分析问题 ，找出这些问题之间的关联（状态转移方程）
4. 讨论底层的边界问题
5. 解决问题（通常使用数组进行迭代求出最优解）
   文字来源

下面这个图是我们离散老师讲的一点动态规划，第一问是最基础的贪心，相信大家都会，第二问的DP如果是初学者建议把图片里的过程看一遍理解一下，（类似01背包）对理解下面的背包有好处。

二.背包九讲

（1）完全背包

考虑有 n 种物品，第 i 种物品的每个重量为 wi，价值为 vi，有无限多个。 我们手头有一个大小为 m的背包，需要算出能装下的最大总价值。

我们设 f(i) 表示大小为 i 的背包最多能装的价值，那么可以得到一个转移方程:$$f(i)=maxf(i-w1)+v1,f(i-w2)+v2,...,f(i-wn)+vn$$写成简洁一些的形式:
$$f(i)=maxf(i-wj)+vj$$初始条件为:
$$f(0)=0$$
尝试用代码来实现:

for (int i = 0; i <= m; ++i) {
    for (int j = 1; j <= n; ++j) {
        if (i - w[j] >= 0)
            f[i] = max(f[i], f[i - w[j]] + v[j]);
    } 
}

交换两重循环的顺序也是可以的:

for (int i = 1; i <= n; ++i) {
    for (int j = w[i]; j <= m; ++j) {
        f[j] = max(f[j], f[j - w[i]] + v[i]); 
    }
}

完全背包是正序，全程贪心的思想用max取最大值
我们总共有 m 个状态，每个状态需要进行 n 次转移，故最终的复杂度为 O(nm)。

P1616 疯狂的采药(完全背包)

P1616 疯狂的采药
LiYuxiang是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。为此，他想拜附近最有威望的医师为师。医师为了判断他的资质，给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同种类的草药，采每一种都需要一些时间，每一种也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。”
如果你是LiYuxiang，你能完成这个任务吗？
此题和原题的不同点：
1.每种草药可以无限制地疯狂采摘。
2.药的种类眼花缭乱，采药时间好长好长啊！师傅等得菊花都谢了！
输入格式
输入第一行有两个整数T（1 <= T <= 100000）和M（1 <= M <= 10000），用一个空格隔开，T代表总共能够用来采药的时间，M代表山洞里的草药的数目。接下来的M行每行包括两个在1到10000之间（包括1和10000）的整数，分别表示采摘某种草药的时间和这种草药的价值。
输出格式
输出一行，这一行只包含一个整数，表示在规定的时间内，可以采到的草药的最大总价值。
输入输出样例
输入

70 3
71 100
69 1
1 2

输出

140

#include
using namespace std;
int dp[100005],tim[100005],vis[100005],t,m,n;
int main()
{
    cin>>t>>m;
    for(int i=0;i<m;i++)
        cin>>tim[i]>>vis[i];
    for(int i=0;i<m;i++)
        for(int j=tim[i];j<=t;j++)
        dp[j]=max(dp[j],dp[j-tim[i]]+vis[i]);//选拿和不拿中最大的那一个（拿的话就要把之前放进去的丢掉空出当前物品的重量）
    cout<<dp[t]<<endl;
    return 0;
}

（2）01背包

将上面的问题稍微进行改动:

考虑有 n 种物品，第 i 种物品的每个重量为 wi，价值为 vi。 每种物品只有 1 件。 有一个大小为 m的背包，需要算出能装下的最大总价值。

我们不能再像刚才那样设计状态了。因为每个物品取过之后就不能再取，所以状态还需要记录物品的相关信息。
考虑如何将问题转化成规模更小的子问题。对于某个物品，在最终的方案中要么不取、要么取，于是我们对这两种情况来分类讨论，转化为子问题:

• 如果没有取第 n 个物品，那么相当于只有前 n − 1 个物品、背包大小相同的子问题;
• 如果取了第 n 个物品，那么相当于只有前 n − 1 个物品（n-1个物品已经经过了了选择）、背包大小减去 w_n 的子问题，在它的答案上再加上 v_n的价值。
  在两种情况中取价值更高的，得到答案。
  状态和转移:
  设 f(i, j) 表示使用编号为 1 ∼ i 的物品，背包容量为 j 时的最大价值， 有转移方程

$$f(i,j)=max(f(i-1,j),f(i-1,j-wi)+vi)$$
初始条件为:
$$f(0,\ast )=0$$

for (int i = 1; i <= n; ++i) {
    for (int j = 0; j <= m; ++j) {
        if (j < w[i])
            f[i][j] = f[i - 1][j];
        else
            f[i][j] = max(f[i - 1][j], f[i - 1][j - w[i]] + v[i]);//f[i-1]是指已经选过i-1件物品了
} }

时间复杂度为 O(nm)。注意到这段代码的空间复杂度也达到了 O(nm)， 在一些问题中无法接受。我们将尝试对它进行优化。

滚动数组

观察刚才的代码:每个 f[i][j] 在转移时只用到了 f[i-1][*]。也 就是说，比 i-1 更小的再也不会被用到。如果把 f 看成一张二维的表 格，那么只有两行的格子是 “活跃” 的。基于这一思想，我们可以只保存这两行。
具体的实现可以参考如下:

int p = 1, q = 0;
for (int i = 1; i <= n; ++i) {
    for (int j = 0; j <= m; ++j) { 
    if (j < w[i])
        f[p][j] = f[q][j];
    else
        f[p][j] = max(f[q][j], f[q][j - w[i]] + v[i]); 
        swap(p, q);//用第一行求出第二行以后，第二行又作为第一行求下一行，每次只用到两行的空间
} }

一维数组

继续刚才的思路:把 f 看成一张二维的表格，那么每个格子在转移时 只会用到上一行中在它左侧的格子。如果我们调整一下转移的顺序，每 一行从右往左进行更新(j 从大到小)，那么 “活跃” 的格子就正好只有上一行的左半部分以及这一行的右半部分。

那么实际上我们只需要保存这些活跃格子的状态就行了。
一维数组
代码实现:

for (int i = 1; i <= n; ++i) {
    for (int j = m; j >= w[i]; --j) {// 倒序！！！
        f[j] = max(f[j], f[j - w[i]] + v[i]); }
}

注意到当 j

P1048 采药（01背包）

P1048 采药
题目描述
辰辰是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。为此，他想拜附近最有威望的医师为师。医师为了判断他的资质，给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同的草药，采每一株都需要一些时间，每一株也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。”
如果你是辰辰，你能完成这个任务吗？
输入格式
第一行有22个整数M(1≤M≤100)，用一个空格隔开，TT代表总共能够用来采药的时间，M代表山洞里的草药的数目。
接下来的M行每行包括两个在1到100之间（包括1和100）的整数，分别表示采摘某株草药的时间和这株草药的价值。
输出格式
1个整数，表示在规定的时间内可以采到的草药的最大总价值。
输入

70 3
71 100
69 1
1 2

输出

3

#include
using namespace std;
const int maxn=1005;
int dp[maxn],w[maxn],vis[maxn],n,m,t;
int main()
{
    cin>>t>>m;
    for(int i=1;i<=m;i++)
        cin>>w[i]>>vis[i];
    for(int i=1;i<=m;i++)
        for(int j=t;j>=0;--j)
            if(j>=w[i])//01倒序完全正序
                dp[j]=max(dp[j],dp[j-w[i]]+vis[i]);
    cout<<dp[t]<<endl;
    return 0;
}

（3）多重背包

在之前的问题基础上，再进行一些改动:

考虑有 n 种物品，第 i 种物品的每个重量为 w_i，价值为 v_i。 第 i 种物品最多能取 c_i 件。 有一个大小为 m的背包，需要算出能装下的最大总价值。

转化为 01 背包
尝试将这个问题转化为我们已知的问题…
对于每种 c_i 个的物品，将它拆成 c_i个 “01 物品”，然后使用 01 背包的算法进行解决。
问题解决了，但代价是什么?但这样的复杂度高达 O(m ∑ ci)，难以接受。

更合理的分组
我们将物品拆分的目的是:使拆分后的物品的选取方法可以表示出拆分前的选取方法。
那么显然刚才的拆分方法产生了大量冗余信息，拆出来的物品都是相同 的，而我们却重复计算了许多相同的选法。这就很不符合 dp 的核心思想。考虑换一种更加合理的、产生更少新物品的分组。

整数拆分（二进制拆分）

给出正整数 n，将 n 分为尽可能少的正整数之和，使得从中选取若干个求和，可以得到 1 ∼ n 的所有整数。
如7=1+2+4，13=1+2+4+6。那么1~13中任意一个数都可以用拆出来的1，2，4，6中的几个数组合相加得到，放到题目中就可以实现所有物品试一遍来比较最大值的优化方案。
首先估计出答案的一个下界:假设分成了 k 个数，那么根据乘法原理， 最多可以表示 2k 个不同的数。于是 2k ≥ n，即k ≥ log2 n
然后可以简单地构造出一个解:

1. 将1,2,4,…,2i 不断地加入集合，直到再加入下一个会导致加起来
   超过 n;
2. 然后将剩下的 n −∑加入集合。
   容易验证，可以组合出所有整数。
   代码实现:

void partition(int n)
{
for (int i = 1; i <= n; i *= 2) {
    /* 将 i 加入答案; */
    n -= i; 
}
if (n > 0) 
{/* 将 n 加入答案; */} 
}

复杂度O(nm log m)

P1776 宝物筛选（多重背包）

P1776 宝物筛选
题目描述
终于，破解了千年的难题。小F 找到了王室的宝物室，里面堆满了无数价值连城的宝物。
这下小 F可发财了，嘎嘎。但是这里的宝物实在是太多了，小 FF 的采集车似乎装不下那么多宝物。看来小 FF 只能含泪舍弃其中的一部分宝物了。

小 F 对洞穴里的宝物进行了整理，他发现每样宝物都有一件或者多件。他粗略估算了下每样宝物的价值，之后开始了宝物筛选工作：小 FF 有一个最大载重为 W 的采集车，洞穴里总共有 n 种宝物，每种宝物的价值为 v_i
，重量为 w_i，每种宝物有 m_i件。小 F 希望在采集车不超载的前提下，选择一些宝物装进采集车，使得它们的价值和最大。
输入格式
第一行为一个整数 n 和 W，分别表示宝物种数和采集车的最大载重。

接下来 nn 行每行三个整数v_i，w_i，m_i。
输出格式
输出仅一个整数，表示在采集车不超载的情况下收集的宝物的最大价值。

#include
using namespace std;
const int maxn=1000005;
int dp[maxn],v[maxn],w[maxn],n,wc,a,b,c,cnt;
int main()
{
    cin>>n>>wc;
    for(int i=0;i<n;i++)
    {
        cin>>a>>b>>c;
        for(int j=1;j<=c;j<<=1)//二进制拆分防止爆炸
        {/*拆成好多个01背包（比如原来是三种拆成15种用cnt计数）*/
            v[++cnt]=a*j;
            w[cnt]=b*j;
            c-=j;
        }
        if(c)v[++cnt]=a*c,w[cnt]=b*c;
    }
    for(int i=1;i<=cnt;i++)
        for(int j=wc;j>=w[i];j--)
            dp[j]=max(dp[j],dp[j-w[i]]+v[i]);//普通的01背包
    printf("%d\n",dp[wc]);
    return 0;
}

（4）二维费用背包

在之前问题的基础上，每个物品有两个维度的费用(例如重量和体积) w_i 和 z_i，均不能超过背包对应的容量。
以 01 背包为例，设 f(i, j, k) 表示使用编号为 1 ∼ i 的物品，背包两个维 度的容量分别为 j 和 k 时的最大价值，有转移方程
$$f(i,j,k)=maxf(i-1,j,k),f(i-1,j-wi,k-zi)+vi$$
空间优化
滚动数组显然是可以的。进一步的优化，想象一个三维的表格，我们发 现 “活跃” 的格子总数不会超过一层，于是可以倒序循环，去掉第一维。

P1507 NASA的食物计划（二维费用背包）

P1507 NASA的食物计划
题目背景
NASA(美国航空航天局)因为航天飞机的隔热瓦等其他安全技术问题一直大伤脑筋,因此在各方压力下终止了航天飞机的历史,但是此类事情会不会在以后发生，谁也无法保证,在遇到这类航天问题时,解决方法也许只能让航天员出仓维修,但是多次的维修会消耗航天员大量的能量,因此NASA便想设计一种食品方案,让体积和承重有限的条件下多装载一些高卡路里的食物.
题目描述
航天飞机的体积有限,当然如果载过重的物品,燃料会浪费很多钱,每件食品都有各自的体积、质量以及所含卡路里,在告诉你体积和质量的最大值的情况下,请输出能达到的食品方案所含卡路里的最大值,当然每个食品只能使用一次.
输入格式
第一行 两个数 体积最大值(<400)和质量最大值(<400)
第二行 一个数 食品总数N(<50).
第三行－第3+N行
每行三个数 体积(<400) 质量(<400) 所含卡路里(<500)
输出格式
一个数 所能达到的最大卡路里(int范围内)

#include
using namespace std;
typedef long long ll;
const ll N=1e3+7;
const ll mod=1e9+7;
ll mv,mw,n,v[N],w[N],c[N],dp[N][N];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    cin>>mv>>mw;
    cin>>n;
    for(int i=1;i<=n;++i)
        cin>>v[i]>>w[i]>>c[i];
    for(int i=1;i<=n;++i)
        for(int j=mv;j>=v[i];--j)
            for(int k=mw;k>=w[i];--k)
            dp[j][k]=max(dp[j][k],dp[j-v[i]][k-w[i]]+c[i]);
    cout<<dp[mv][mw]<<endl;
    return 0;
}

（5）混合背包

将刚才的 01 背包、多重背包、完全背包进行混合，有的物品只能取有限个，有的可以任意取，怎么解决这个问题呢?
一个简单粗暴的方法是，将所有的物品都当成多重物品(考虑取的个数上限)，然后按照多重背包来做。复杂度 O(nm log m)。
如果只有 01 物品和无限物品，那么可以使用一维数组，遇到 01 物品时 倒序循环，遇到无限物品时正序循环。复杂度 O(nm)。

P1833樱花（混合背包）

P1833樱花
题目描述
爱与愁大神后院里种了n棵樱花树，每棵都有美学值C_i。爱与愁大神在每天上学前都会来赏花。爱与愁大神可是生物学霸，他懂得如何欣赏樱花：一种樱花树看一遍过，一种樱花树最多看A_i遍，一种樱花树可以看无数遍。但是看每棵樱花树都有一定的时间T_i 。爱与愁大神离去上学的时间只剩下一小会儿了。求解看哪几棵樱花树能使美学值最高且爱与愁大神能准时（或提早）去上学。
输入格式
共n+1行：
第1行：三个数：现在时间Ts（几点：几分），去上学的时间Te（几点：几分），爱与愁大神院子里有几棵樱花树n。

第2行~第n+1行：每行三个数：看完第i棵树的耗费时间Ti，第i棵树的美学值Ci，看第i棵树的次数Pi（Pi=0表示无数次，Pi是其他数字表示最多可看的次数Pi）。

输出格式
只有一个整数，表示最大美学值。

#include
using namespace std;
const int maxn=1000005;
int w[maxn],vis[maxn],c,nx,ny,ex,ey,n,m,cnt,a,b,dp[maxn];
int main()
{
    scanf("%d:%d%d:%d%d",&nx,&ny,&ex,&ey,&n);//scanf()的妙用
    int tim=(ex*60+ey)-(nx*60+ny);
    for(int i=1;i<=n;i++)
    {
        cin>>a>>b>>c;
        if(!c)c=999999;
        for(int j=1;j<=c;j<<=1)
        {
            vis[++cnt]=b*j;
            w[cnt]=a*j;
            c-=j;
        }
        if(c)vis[++cnt]=c*b,w[cnt]=c*a;
    }
    for(int i=1;i<=cnt;i++)
        for(int j=tim;j>=w[i];j--)
        dp[j]=max(dp[j],dp[j-w[i]]+vis[i]);
    cout<<dp[tim]<<endl;
    return 0;
}

（6）分组背包

在 01 背包的基础上，每个物品属于一个组，每组中的物品是互斥的 (最多只能取一件)。
考虑把每个组当成一个 “物品”，可以取其中的一个，或者不取。
设 f(i, j) 表示对于前 i 组物品，使用容量为 j 的背包，可以装的最大价
值。那么转移方程为
$$f(i,j)=max(f(i-1,j),f(i-1,j-wk)+vk)k\in Gi$$
也可以优化成一维数组

P1757 通天之分组背包（分组背包）

P1757 通天之分组背包
题目描述
自01背包问世之后，小A对此深感兴趣。一天，小A去远游，却发现他的背包不同于01背包，他的物品大致可分为k组，每组中的物品相互冲突，现在，他想知道最大的利用价值是多少。
输入格式
两个数m,n，表示一共有n件物品，总重量为m

接下来n行，每行3个数ai,bi,ci，表示物品的重量，利用价值，所属组数

输出格式
一个数，最大的利用价值

输入输出样例
输入

45 3
10 10 1
10 5 1
50 400 2

输出

10

#include
using namespace std;
const int maxn=100005;
int dp[1005][005],w[maxn],vis[maxn],d[maxn],f[maxn],n,m,t,x,num=0;
int main()
{
    std::ios::sync_with_stdio(false);
    cin>>m>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>w[i]>>vis[i]>>x;
        num=max(num,x);
        ++d[x];
        dp[x][d[x]]=i;
    }
    for(int k=1;k<=num;k++)
        for(int j=m;j>=0;j--)
            for(int i=1;i<=d[k];i++)
            {
                int xx=dp[k][i];
                if(j>=w[xx])
                    f[j]=max(f[j],f[j-w[xx]]+vis[xx]);
            }

    cout<<f[m]<<endl;
    return 0;
}

（7）树形背包

在 01 背包的基础上，每个物品可能依赖于某个其他物品(需要选那个 物品，才能选这个物品)，并且这个依赖关系构成一棵树。
有时候，可能有多个物品没有依赖，可以增加一个重量和价值为 0 的虚 拟物品，将它作为这些物品的依赖，从而构成一棵树。

1.dfs 序

对于一棵有根树，我们从树根开始进行 dfs，按照遇到结点的顺序给结 点重新编号，称为 dfs 序(先序)，那么有如下性质:
对于每棵子树，树根在 dfs 序列中最先出现 一棵子树在 dfs 序中对应连续的一段区间

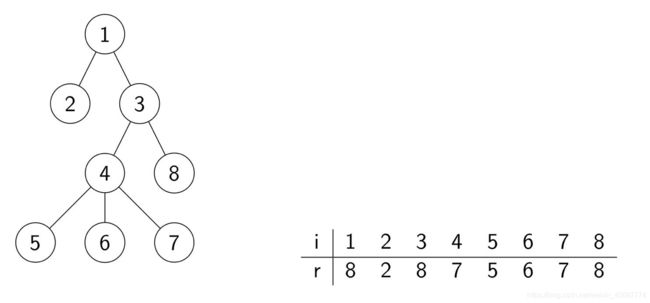
2.利用 dfs 序解决树形背包

得到 dfs 序之后，我们就可以解决树形背包问题了。按照 dfs 序从后往 前，对于每件物品，考虑它选/不选的两种情况:
如果不选，那么它对应的整棵子树也不能选，变成(dfs 序中它子树 右侧的下一个)的子问题;
如果选，就变成(dfs 序中它的下一个)的子问题。
设 f(i, j) 表示对于 dfs 序中 i ∼ n 的物品，容量为 j 的背包，最多能装的
价值。设结点 i 在 dfs 序中子树最后一个的结点为 ri，则有转移方程 f(i,j) = max{f(ri + 1,j),f(i + 1,j − wi) + vi}
时间复杂度为 O(nm)。

P2014 选课(树形背包)

题目描述
在大学里每个学生，为了达到一定的学分，必须从很多课程里选择一些课程来学习，在课程里有些课程必须在某些课程之前学习，如高等数学总是在其它课程之前学习。现在有 N 门功课，每门课有个学分，每门课有一门或没有直接先修课（若课程a是课程b的先修课即只有学完了课程a，才能学习课程b）。一个学生要从这些课程里选择 M 门课程学习，问他能获得的最大学分是多少？

输入格式
第一行有两个整数 N , M 用空格隔开。(1≤M≤300)

接下来的 N行,第 I+1 行包含两个整数k _i 和 s _i ,k _i 表示第I门课的直接先修课，s _i
​表示第I门课的学分。若 k _i=0 表示没有直接先修课（1≤k _i≤N , 1≤s _i ≤20）。
输出格式
只有一行，选 M 门课程的最大得分。
输入：

7  4
2  2
0  1
0  4
2  1
7  1
7  6
2  2

输出：

13

P1064 金明的预算方案(树形背包/分组背包)

（8）方案数问题凡是求方案数的问题一定都需要初始化（dp[0]=1）

1.P1164 小 A 点菜

题目描述
不过uim由于买了一些辅（e）辅（ro）书，口袋里只剩M元(M≤10000)。餐馆虽低端，但是菜品种类不少，有N种(N≤100)，第ii种卖a_i 元(a _i≤1000)。由于是很低端的餐馆，所以每种菜只有一份。小A奉行“不把钱吃光不罢休”，所以他点单一定刚好吧uim身上所有钱花完。他想知道有多少种点菜方法。
由于小A肚子太饿，所以最多只能等待1秒。
输入格式
第一行是两个数字，表示N和M。
第二行起N个正数a _i
（可以有相同的数字，每个数字均在1000以内）。
输出格式
一个正整数，表示点菜方案数，保证答案的范围在int之内。

输入

4 4
1 1 2 2

输出

3

与 01 背包很类似，只是变成了计数问题。
设f(i,j)表示使用编号为1∼i的菜，花完j元的方法数; 得到转移方程

$$f(i,j)=f(i-1,j)+f(i-1,j-ai)$$
当前情况的方案总数应该是所有能到达当前位置途径的方案数的总和（递推）
注意初始条件是$$f(0,0)=1,f(0,\ast )=0$$
也可把二维转换为一维，运用滚动数组，每次都只用到了i-1所以只需一维即可（类似01背包所以要倒序）初始条件也将改成dp[0]=1，即花0元的方案数为1（什么都不买）

#include
using namespace std;
const int maxn=1e4;
int a[maxn],dp[maxn],n,m;
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        cin>>a[i];
    dp[0]=1;
    for(int i=1;i<=n;i++)
        for(int j=m;j>=a[i];j--)
        dp[j]+=dp[j-a[i]];//
    cout<<dp[m]<<endl;
    return 0;
}

2.P1466 集合

将 1 ∼ n 的整数分为两个集合，使它们的总和相等。求本质不同的方案数。n ≤ 39 由于所有的数的总和一定，两个集合的和相等就意味着它们都等于 n(n+1) /4;
于是问题变为从 1 ∼ n 中选若干个数，使它们的和为 n(n+1) /4;
dp[i]代表和为i的方案数
注意最后答案要除以二，因为重复不算

#include
using namespace std;
typedef long long ll;
const ll N=1e3+7;
const ll mod=1e9+7;
ll n,dp[N];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    cin>>n;
    ll sum=n*(n+1)/2;
    if(sum&1){cout<<0<<endl;return 0;}
    dp[0]=1;
    for(int i=1;i<=n;++i)
    {
        for(int j=sum;j>=i;j--)
        {
            dp[j]+=dp[j-i];
        }
    }
    cout<<dp[sum/2]/2<<endl;
}

二. DP简单应用

[nico和niconiconi]

题目描述

“にっこにっこにー” ——nico
nico平时最喜欢说的口头禅是niconiconi~。
有一天nico在逛著名弹幕网站"niconico"的时候惊异的发现，n站上居然有很多她的鬼畜视频。其中有一个名为《让nico为你洗脑》的视频吸引了她的注意。
她点进去一看，就被洗脑了:“niconicoh0niconico*^vvniconicoG(vniconiconiconiconiconicoG(vniconico…”
弹幕中刚开始有很多“nico1 nico2”等计数菌，但到后面基本上都是“计数菌阵亡”的弹幕了。
nico也想当一回计数菌。她认为：“nico” 计 a 分，“niconi” 计 b 分，“niconiconi” 计 c 分。
她拿到了一个长度为 n 的字符串，请帮她算出最大计数分数。
注：已被计数过的字符不能重复计数！如"niconico"要么当作"nico"+“nico"计a+b 分，要么当作"niconi”+"co"计 c 分。
输入描述:
第一行四个正整数 。
第二行是一个长度为 n 的字符串。
输出描述:
一个整数，代表最大的计数分数。

示例1
输入

19 1 2 5
niconiconiconiconi~

输出

7

说明
"niconi"co"niconiconi"~故为2+5=7分
思路
比较简单的dp
计 dp[i]dp[i] 代表前 ii 个字符的计数最大值。
那么可得转移方程：
$$if(substr(i-4,4)==nico)thendp[i]=max(dp[i],dp[i-4]+a)$$$$if(substring(i-6,6)==niconi)thendp[i]=max(dp[i],dp[i-6]+b)$$$$if(substring(i-10,10)==niconiconi)thendp[i]=max(dp[i],dp[i-10]+c)$$
substr()函数详解
最后输出 dp[n] 即可。

#include
using namespace std;
typedef long long ll;
const ll N=3e5+7;
const ll mod=1e9+7;
ll n,a,b,c,dp[N];
string s;
int main()
{
    cin>>n>>a>>b>>c;
    cin>>s;
    for(int i=0;i<=n;i++)
    {
        string s1="",s2="",s3="";
        if(i>=4)s1=s.substr(i-4,4);
        if(i>=6)s2=s.substr(i-6,6);
        if(i>=10)s3=s.substr(i-10,10);
        if(s1=="nico")dp[i]=max(dp[i],dp[i-4]+a);
        else dp[i]=max(dp[i],dp[i-1]);
        if(s2=="niconi")dp[i]=max(dp[i],dp[i-6]+b);
        else dp[i]=max(dp[i],dp[i-1]);
        if(s3=="niconiconi")dp[i]=max(dp[i],dp[i-10]+c);
        else dp[i]=max(dp[i],dp[i-1]);
    }
    cout<<dp[n]<<endl;
}

输出：

2

思路：

先将元素按能量值排序，下文默认已排序。

可以证明存在一个最优方案，满足每个魔法一定消耗一段连续的元素。

注意是至少取 k段，那么从 k+1开始DP

定义 dp[i]代表：前i项最优解dp[i]代表：前i项最优解 dp[i]代表：前 i 项最优解dp[i]代表：前i项最优解，那么可以得到，对于任意位置：

是拓展前面，从长度 m变成 m+1；(数学归纳法思想，任意位置肯定都是合法的，m>=k成立)(数学归纳法思想，任意位置肯定都是合法的，m>=k成立) (数学归纳法思想，任意位置肯定都是合法的，m>=k成立)(数学归纳法思想，任意位置肯定都是合法的，m>=k成立)
断开前面，从当前位置往前 k−1项，和当前第 i 项，组成长度为 k 的序列。

时间复杂度O(N−K)

#include
using namespace std;
#define Pi acos(-1.0)
typedef long long ll;
const ll N=3e5+7;
const ll mod=1e9+7;
ll n,k,dp[N],a[N];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    cin>>n>>k;
    for(int i=1;i<=n;++i)
        cin>>a[i],dp[i]=mod;
    sort(a+1,a+1+n);
    dp[k]=a[k]-a[1];
    for(int i=k+1;i<=n;++i)//至少要选k个那么从k+1开始DP
        dp[i]=min(dp[i-1]+a[i]-a[i-1],dp[i-k]+a[i]-a[i-k+1]);
    cout<<dp[n]<<endl;//对于第i个魔法，要么跟着上一组做，要么另起炉灶新开一组，用min取最小值
    return 0;
}

缺席的神官

广工的腾讯杯，是真的NB，一套题附赠一篇小说
题目描述
面前的巨汉，让我想起了多年前的那次，但这个巨汉身上散布着让人畏惧害怕的黑雾。即使看不到脸，但是威严却在这个从者身边不断围绕。 「吾乃七骑之中的骑士(rider)，你们就是御主所说的阻扰者吧」 「是」我从雪茄盒里面掏出一根雪茄，想稍微冷静一下。 「那便无需多言了」和我签订了暂时契约的理查一世倒是直接拔剑了，如此看来查理一世的职介就是剑士(saber)。 「我看你的御主倒是没有这个想法吧」 他似乎看出了我的想法，虽然只是亡魂的影子，但也曾是人，能洞察人心。 「您是这样的想法吗」理查一世把剑收了起来。 「是啊，虽然参与圣杯战争的御主和从者目的是实现愿望，但既然是残缺的圣杯，我也会猜想是否从者对圣杯的渴望并没有那么高，是否有值得交涉的余地」 「哈」巨汉笑了，「真是大胆的妄想啊，但你应该明白圣杯显现的方法吧，所以这一切都是不可避免的。但我也不想使用武力，解答我的困惑吧，魔术师，如果你们能回答出来，我就会放弃」 「我明白了，洗耳恭听」 「古时有一个懒惰的祭司，而祭司在连续m天内必须一直去神庙内工作，但祭司的怠惰在诱惑着祭司，于是祭司决定这段时间内只选出k个连续的时间段去神庙工作，但是高级祭司(祭司的上级)又会定期对神庙内的工作人员进行点名。祭司不想因此失去这份工作，所以提前知道了高级祭司会点名n次以及每次点名的日子。所以祭司把点名的日子纳入工作的日子当中的同时又尽可能的偷懒。那么，这个祭司到底工作了多少天呢」 「这个答案很简单，荷鲁斯」
输入描述:
第一行输入三个整数n,m,k (1 <= n <= 2000) (n <= m <= 109) (1<= k <= n)，分别为高级祭司的点名次数,原本需要工作的天数和懒惰的祭司的工作次数。第二行输入n个数字ai (1 <= ai <= m),为高级祭司检查的日期。输入保证对于任意的i,j (1<= i 输出描述:
输出懒惰的祭司进行工作的最少天数

#include
#define debug cout<<"ok"<
typedef long long ll;
const int maxn=1e5+10;
const int mod=1e9+7;
using namespace std;
int n,m,k;
ll dp[2019][2019],a[maxn];
int main()
{
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);//加速cin;
    cin>>n>>m>>k;
    for(int i=1;i<=n;i++)
        cin>>a[i];
    for(int i=0;i<=n;i++)
        for(int j=0;j<=k;j++)//全部置INF；
            dp[i][j]=1e10;
    dp[0][0]=0;//初始化
    for(int i=1;i<=n;i++)//N件东西
        for(int j=1;j<=k;j++)//取K次
            dp[i][j]=min(dp[i-1][j-1],dp[i-1][j]+a[i]-a[i-1]);//取最小值；
    cout<<dp[n][k]+k<<endl;//要加k每次算a[i]-a[i-1]时都少了1，少K次；
    return 0;
}

篇幅所限，放一下我的博客链接，我自己写的博客哦！

三.LCS最长公共子序列

LCS最长公共子序列

四.棋盘型高维（三维）动态规划

棋盘型高维动态规划

五.区间DP

我自己写的博客哦！
区间DP入门

六.前缀DP

七.树形DP

【树形DP】树的重心详解+多组例题详解

八.状压DP

我自己写的博客哦！
【状压DP】状态压缩动态规划入门超详解

九.斜率优化DP

待更！待学

十.概率DP/期望DP

概率DP/期望DP

动态规划：DP从入门到破门而出（入门必刷例题）

注：如果您通过本文,有(qi)用(guai)的知识增加了，请您点个赞再离开,如果不嫌弃的话,点个关注再走吧，日更博主每天在线答疑 ! 当然，也非常欢迎您能在讨论区指出此文的不足处，作者会及时对文章加以修正 !如果有任何问题，欢迎评论，非常乐意为您解答！( •̀ ω •́ )✧