2019CCPC湘潭全国邀请赛题解

目录

 

【正赛情况】 ​

【A. Chessboard】

【B. Build Tree】

【C. Chika and Friendly Pairs 】

【D. Chika and Solid Geometry】

【E.Hello XTCPC】

【F. Neko and function】

【G. Neko and quadrilateral】

         【H. Neko and sequence】

【I. Neko and tree】

【J. Neko and triangle】

【K. SSY and JLBD】

【L. Can you raed it croretcly?】

---

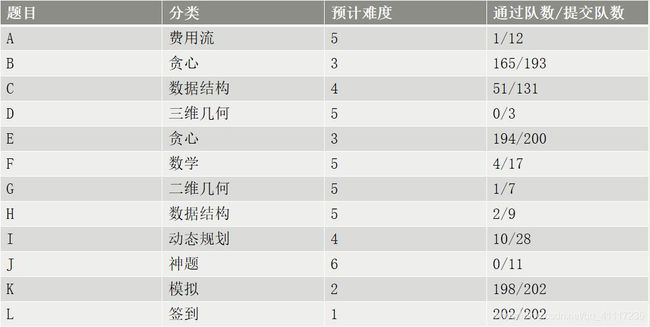
【正赛情况】 

【A. Chessboard】

费用流。        

离散化坐标，每行用一个点表示，每列也用一个点表示。表示第i-1行的点向表示第i行的点连边，容量为第i行及以后能拿的棋子数的上限，费用为0，同理表示相邻列的点两两连边。若第i行第j列上有棋子，则表示第i行的点向表示第j列的点连边，容量为1，费用为该棋子的价值。可以定义源点表示第0行，汇点表示第0列，源点到汇点的最大费用流即为答案。

【B. Build Tree】

题解： Build Tree（树）

【C. Chika and Friendly Pairs 】

题解： Chika and Friendly Pairs（离散化+莫队+树状数组）

【D. Chika and Solid Geometry】

题意：求底面均在z=0平面上，顶点的z坐标大于零的斜圆锥和棱锥的体积并。 将每个z轴方向的横截面看做多边形和圆的面积并，然后对z轴做辛普森积分即可。 多边形和圆的面积并：面积和-面积交。 多边形和圆的面积交：将圆心移动到原点，以原点为基准对多边形进行三角剖分，转化成计算圆心在原点的圆和有一个顶点在原点的三角形的面积交问题。这个进行大力分类讨论即可，细节比较多。

【E.Hello XTCPC】

题解： Hello XTCPC（贪心 or 思维）

【F. Neko and function】

设g(n,k)为k个>=1的数的乘积为n的方案数 很容易推出容斥f(n,k)= sum (-1)^i * g(n,k-i) * C(k,i) 而g(n,k)=prod C(ai+k-1,k-1) 其中n=prod pi^ai pi是n的第i个质因子 可以发现g(n,k)是积性函数，套min-25筛即可。

【G. Neko and quadrilateral】

求面积最大和最小四边形，通过对角线变换为求面积最大和最小三角形 求出任意两点组成的向量，然后排序 枚举向量，基于此进行贪心，维护向量左侧的点到向量的距离单调，右侧的点到向量的距离单调 然后选择最远和最近点更新答案 复杂度n^2logn

【H. Neko and sequence】

考虑如果两种括号都存在，那么移动一定步数后，都会在()上来回移动，可以预处理出每个位置移动多少步后会进入这个循环，或者永远不进入循环 在进入循环之前一定都是朝一个方向一直移动 那么在进入循环之前，起点为i的位置走j步到达的点就是(i+kj)%n 化简为(i+kj%n)%n，设d=kj%n,把区间询问以n-d为间隔分成两部分处理即可，可以用树状数组维护出来 进入循环后的部分也可以按j的奇偶用树状数组轻松维护出来 总体复杂度nlogn

【I. Neko and tree】

树形dp。
dp[i][j]表示以i为根的子树中到i最远的关键点距离为j的方案数。当u向fa[u]更新时，进行更新即可

可以用前缀和分两段优化。
求答案时考虑反过来求，用总方案数减去不合法方案数。不合法方案数在可在更新的时候用类似的方法同时求出。

题解：Neko and tree        I Neko and tree 树形dp

【J. Neko and triangle】

本质上是给你x，y，找到一个区间[l,r]使得 sum_x(l,r)*y-sum_y(l,r)*x最大 如果把所有sum_x(l,r)和sum_y(l,r)映射成二维平面上的点集的话，我们可以发现答案一定在点集的凸壳上 如果求出这个凸壳，就可以二分答案了 这个凸壳可以用分治+闵可夫斯基和来求。

【K. SSY and JLBD】

题解： SSY and JLBD （模拟）

【L. Can you raed it croretcly?】

题解： Can you raed it croretcly? （简单题）