AP聚类以及matlab实现

kmeans聚类以及fcm聚类的一大局限是需要提前知道大致的聚类个数，现实中使用比较受限，2007年，Frey和Dueck在Science发表了《Clustering by Passing Messages Between Data Points》，提出了AP聚类的方法，此方法采用点点之间交换信息的方式聚类，下面对此算法进行分析并且用matlab实现之。

1.算法原理

首先我们定义三个矩阵:

1.相似度矩阵s(i,k)：表示数据点k作为数据点i的聚类中心的能力（相当于k是参选人，i是选民），可以用欧氏距离来表示。

2.吸引度矩阵r(i,k)：表示普通数据点传送到临时聚类中心k的信息，表示k适合作为数据点i的聚类中心的程度。

3.归属度矩阵a(i,k)：表示k传送到i的信息，表示i选择k作为其数据点的合适程度

初始a(i,k)=0，接下来，r(i,k)采用下面规则更新：

r(i,k)=s(i,k)-max{a(i,k’)+s(i,k’)}(k’ s.t k’≠k)

解释：两个点i和k的吸引度是一个相对的概念，我们只需要找到最大的i和k‘的认可程度(a(i,k’)+s(i,k’))，再用s(i,k)与他相减就可以得到k对于i的吸引度了。

a(i,k)采用下面规则更新：

a(i,k)=min{0,r(k,k)+∑max{0,r(i’,k)}

解释：如果k作为其他点i’的聚类中心的合适度很大，那么节点k作为i的聚类中心的何时也可能会较大由此可以先计算出k对于其他节点的适应度(r(i’,k))，然后累加

a(k,k)=∑max{0,r(i’,k)}

解释：即点k在这些吸引度大于0的数据点的支持下，数据点i选择k作为其聚类中心的累计证明。

对于点i，计算a(i,k)+r(i,k)取最大值的k值，如果k=i时，则i作为一个聚类中心，否则确定k是点i的聚类中心，与kmeans算法类似，当聚类中心的值不再变动时认为聚类成功。

伪代码：

​ 1) 初始s,r,a矩阵

​ 2) 更新r,a矩阵

​ 3) 重复12直到达到迭代上限或是误差小于给定值

算法图如下：

2. 代码展示

colorp={'g.','r.','c.','m.','y.','k.'};
color={'g','r','c','m','y','k'};
point={'+','o','*','x','square','diamond'};
n=length(X);
S=zeros(n,n);
%初始化吸引度矩阵s
for i = 1:n
    for j =1:n
        S(i,j)=norm([X(1,i),X(2,i)]-[X(1,j),X(2,j)]);
    end
end

N=size(S,1);A=zeros(N,N);R=zeros(N,N); %初始化矩阵
S=S+1e-12*randn(N,N)*(max(S(:))-min(S(:)));
lam=0.5;
for iter = 1:100
    Rold = R;
    AS=A+S; [Y,I]=max(AS,[],2);
    for i = 1:N
        AS(i,I(i))=-realmax;
    end
    [Y2,I2]=max(AS,[],2);
    R=S-repmat(Y,[1,N]);
    for i = 1:N
        R(i,I(i))=S(i,I(i))*Y2(i);
    end
    R=(1-lam)*R+lam*Rold;
    Aold=A;
    Rp=max(R,0);
    for k = 1:N
        Rp(k,k)=R(k,k);
    end
    A=repmat(sum(Rp,1),[N,1])-Rp;
    dA=diag(A);A=min(A,0);
    for k = 1:N
        A(k,k)=dA(k);
    end
    A=(1-lam)*A+lam*Aold;
end
E=R+A;
I=find(diag(E)>0);K=length(I);
[tem,c] = max(S(:,I),[],2); c(I)=1:K; idx=I(c);


%画图
u=unique(idx);
for i = 1:length(u)
    t=idx==u(i);
    plot(X(1,t),X(2,t),colorp{i});
    hold on;
end

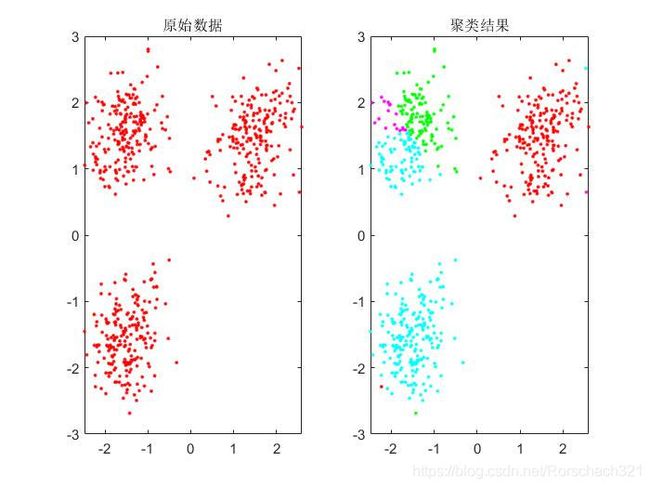
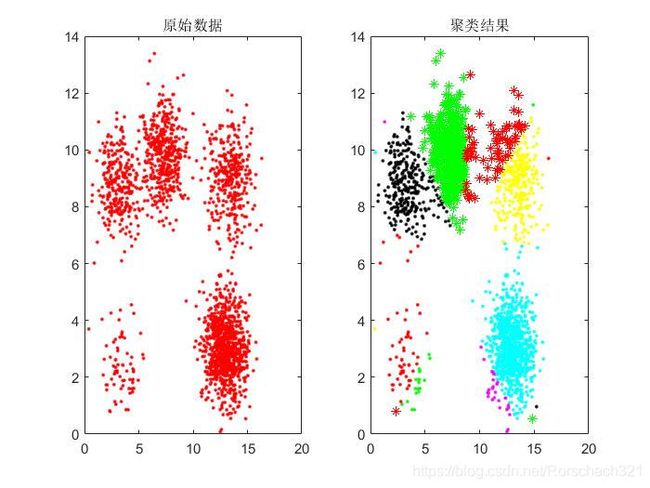
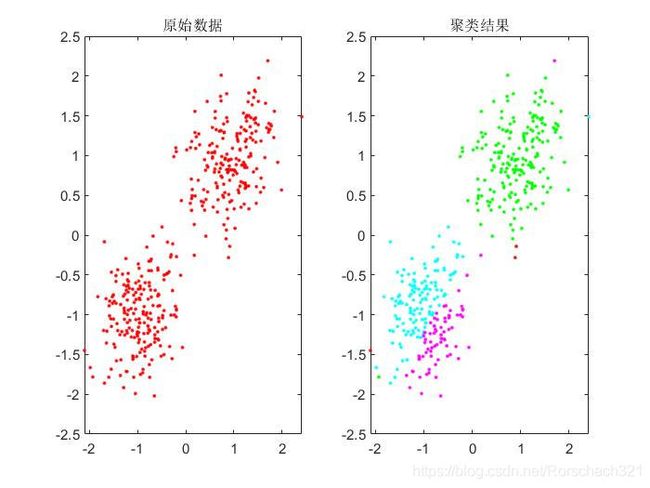
3. 结果展示

参考文献：[2007] Clustering by Passing Messages Between Data Points BrendanJ.Frey*andDelbertDueck