MIT 线性代数（16—18）读书笔记

第十六讲 投影矩阵(Ax=b)和最小二乘法

---

上一讲中，我们知道了投影矩阵$P=A(A^{T}A{)}^{-1}{A}^T$，$Pb$将会把向量投影在$A$的列空间中。即只要知道矩阵$A$的列空间，就能得到投影矩阵$P$的导出式。
##1.投影矩阵（Ax=b无解的情形）

1.1两个极端的例子：

1. 如果$b\in C(A)$，则$Pb=b$；
2. 如果$b\perp C(A)$，则$Pb=0$。

证明1：$$\begin{gathered} Pb=A(A^{T}A{)}^{-1}{A}^{T}b \\ =A(A^{T}A{)}^{-1}{A}^{T}Ax \\ =A((A^T{A}^{-1})A^{T}A)x=Ax=b \end{gathered}$$
证明2：$$\begin{gathered} Pb=A(A^{T}A{)}^{-1}{A}^{T}b \\ =A(A^T{A}^{-1})(A^{T}b) \\ =A((A^T{A}^{-1})0=0 \end{gathered}$$
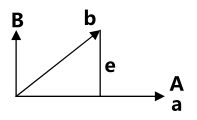
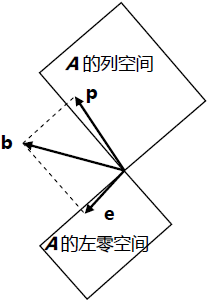
一般情况下，$b$将会有一个垂直于$A$的分量，有一个在$A$列空间中的分量，投影的作用就是去掉垂直分量而保留列空间中的分量。

1.2一般情形

一般情况下，$b$将会有一个垂直于$A$的分量，有一个在$A$列空间中的分量，投影的作用就是去掉垂直分量而保留列空间中的分量。如图：

向量$b投影后，有b=e+p,p=Pb,e=(I-P)b，这里的p是b在C(A)中的分量，而e是b在N(A^T)中的分量。$
可以理解为：向量$b$的投影在$A$的column space，error vector的投影在left null space上，我们知道$P$，可以将$b$ 投影到$p$，那么一个什么样的投影矩阵把$b$投影到了$e$？因为column space与left null space正交补，所以他们共同组成了整个空间，$I$的column space就是整个空间，$I-P$就是把$b$投影到$e$的矩阵，它和$P$有意义的性质。

2. 最小二乘法（Ax=b）

---

回到上一讲最后提到的例题：
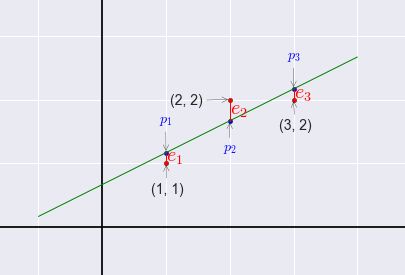
我们需要找到距离图中三个点 $(1,1),(2,2),(3,2)$ 偏差最小的直线：$y=C+Dt$。

根据条件可以得到方程组
$\{\begin{array}{ll}C+D& =1\\ C+2D& =2\\ C+3D& =2\end{array}$
，写作矩阵形式 $\left[\begin{array}{cc}1& 1\\ 1& 2\\ 1& 3\end{array}\right]\left[\begin{array}{c}C\\ D\end{array}\right]=\left[\begin{array}{c}1\\ 2\\ 2\end{array}\right]$，也就是我们的$Ax=b$，很明显方程组无解。
此时我们要找到最接近的解"最优解"，我们要使得解最优即误差最小，定义误差为$Ax-b=e$的模长的平方即$\Vert Ax-b{\Vert }_2=\Vert e{\Vert }_2=e_{21}+e_{22}+e_{23}$。此处使用平方的原因一是排除开根号带来的非线性运算，一是方便利用偏导数求解最小值。

---

• 1.利用偏导求解

这里如果使用偏导数我们也能得到关于最优解的方程，展开结果为:
$\{\begin{array}{ll}\Vert e{\Vert }_2& =e_1^2+e_2^2+e_2^2\\ & =(C+D-1{)}^2+(C+2D-2{)}^2+(C+3D-2{)}^2\\ & =3C^2+14D^2+9-10C-22D+12CD\end{array}$
然后对$C$求偏导为$6C-10+12D=0$；对$D$求偏导为$28D-22+12C=0$。
解方程得$\hat{C}=\frac{2}{3},\hat{D}=\frac{1}{2}$，则“最佳直线”为$y=\frac{2}{3}+\frac{1}{2}t$，带回原方程组解得$p_1=\frac{7}{6},p_2=\frac{5}{3},p_3=\frac{13}{6}$，即$e_1=-\frac{1}{6},e_2=\frac{1}{3},e_3=-\frac{1}{6}$。
于是我们得到$p=\left[\begin{array}{c}\frac{7}{6}\\ \frac{5}{3}\\ \frac{13}{6}\end{array}\right],e=\left[\begin{array}{c}-\frac{1}{6}\\ \frac{1}{3}\\ -\frac{1}{6}\end{array}\right]$，易看出$b=p+e$，同时我们发现$p\cdot e=0$即$p\perp e$。

可以验证，向量p 与e 正交，并且e 与矩阵A 的列空间正交。
$$\begin{gathered} p^{T}e=7/6\ast (-1/6)+5/3\ast 1/3+13/6\ast (-1/6)=0 \\ {e}^T{a}_1=1\ast (-1/6)+1\ast 1/3+1\ast (-1/6)=0 \\ {e}^T{a}_2=1\ast (-1/6)+2\ast 1/3+3\ast (-1/6)=0 \end{gathered}$$

误差向量$e$不仅垂直于投影向量$p$，它同时垂直于列空间，如 $\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right],\left[\begin{array}{c}1\\ 2\\ 3\end{array}\right]$。

• 2.利用矩阵求解

用矩阵的方法求解$A\hat{x}=Pb$得到的方程是一样的，现在我们尝试解出$\hat{x}=\left[\begin{array}{c}\hat{C}\\ \hat{D}\end{array}\right]$与$p=\left[\begin{array}{c}{p}_1\\ p_2\\ p_3\end{array}\right]。$
$$\begin{gathered} A^{T}A\hat{x}=A^{T}b \\ {A}^{T}A=\left[\begin{array}{cc}3& 6\\ 6& 14\end{array}\right]A^{T}b=\left[\begin{array}{c}5\\ 11\end{array}\right] \\ \left[\begin{array}{cc}3& 6\\ 6& 14\end{array}\right]\left[\begin{array}{c}\hat{C}\\ \hat{D}\end{array}\right]=\left[\begin{array}{c}5\\ 11\end{array}\right] \end{gathered}$$

写成方程形式为$\{\begin{array}{ll}3\hat{C}+16\hat{D}& =5\\ 6\hat{C}+14\hat{D}& =11\end{array}$，也称作$正规方程组（normalequations）$。
求的的结果是一样的。

我们现在做的运算也称作$线性回归（linearregression）$，使用误差的平方和作为$测量总误差的标准$。

• 注：
  如果有另一个点，如$(0,100)$，在本例中该点明显距离别的点很远，最小二乘将很容易被离群的点影响，$通常使用最小二乘时会去掉明显离群的点$。

3.证明$A^{T}A$可逆

---

###3.1 证明可逆
接下来我们观察$A^{T}A$，$如果A的各列线性无关，求证A^{T}A是可逆矩阵$。
先假设$A^{T}Ax=0$，两边同时乘以$x^T$有$x^T{A}^{T}Ax=0$，即$(Ax{)}^T(Ax)=0$。一个矩阵乘其转置结果为零，则这个矩阵也必须为零（$(Ax{)}^T(Ax)$相当于$Ax$长度的平方）。则$Ax=0$，结合题设中的“$A$的各列线性无关”，可知$x=0$，也就是$A^{T}A$的零空间中有且只有零向量，得证。

###3.2互相垂直线性无关
我们再来看一种线性无关的特殊情况：$互相垂直的单位向量一定是线性无关的$。
比如：$\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right]\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$，这三个正交单位向量也称作标准正交向量组（orthonormal vectors）。
另一个例子$\left[\begin{array}{c}\cos \theta \\ \sin \theta \end{array}\right]\left[\begin{array}{c}-\sin \theta \\ \cos \theta \end{array}\right]$
下一讲研究标准正交向量组。

4.总结

---

1.记住图的意义：

2.最小二乘法求解的意义。
3.$A^{T}A$可逆的条件和正交向量组。

---

#第十七讲：正交矩阵和Gram-Schmidt正交化法

---

这是关于正交性最后一讲，已经知道正交空间，比如行空间和零空间，今天主要看正交基和正交矩阵

1.标准正交基与正交矩阵

---

###1.1 标准正交基

1. 定义**$标准正交向量$（orthonormal）：$q_i^T{q}_j=\{\begin{array}{l}0i\ne j\\ 1i=j\end{array}$;
   2.将标准正交向量放入矩阵中，有$Q=[q_1{q}_2\cdots q_n]$,计算$Q^{T}Q$
   $$Q^{T}Q=\left[\begin{array}{cccc}1& 0& \cdots & 0\\ 0& 1& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & 1\end{array}\right]=I$$
   我们也把$Q$成为$标准正交矩阵$**（orthonormal matrix）。

标准正交基：

• 举个置换矩阵的例子：$Q=\left[\begin{array}{ccc}0& 1& 0\\ 1& 0& 0\\ 0& 0& 1\end{array}\right]$，则$Q^T=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 1& 0& 0\end{array}\right]$，易得$Q^{T}Q=I$。
• 使用上一讲的例子$Q=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]$，列向量长度为$1$，且列向量相互正交。
• 其他例子$Q=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1& 1\\ 1& -1\end{array}\right]$，列向量长度为$1$，且列向量相互正交。
• 使用上一个例子的矩阵，令$Q^{\prime }=c\left[\begin{array}{cc}Q& Q\\ Q& -Q\end{array}\right]$，取合适的$c$另列向量长度为$1$也可以构造标准正交矩阵：$Q=\frac{1}{2}\left[\begin{array}{cccc}1& 1& 1& 1\\ 1& -1& 1& -1\\ 1& 1& -1& -1\\ 1& -1& -1& 1\end{array}\right]$，这种构造方法以阿德玛（Adhemar）命名，对$2,4,16,64,\cdots$阶矩阵有效。
• 再来看一个例子，$Q=\frac{1}{3}\left[\begin{array}{ccc}1& -2& 2\\ 2& -1& -2\\ 2& 2& 1\end{array}\right]$，列向量长度为$1$，且列向量相互正交。格拉姆-施密特正交化法的缺点在于，由于要求得单位向量，所以我们总是除以向量的长度，这导致标准正交矩阵中总是带有根号，而上面几个例子很少有根号。

**标准正交矩阵 **

$Q^{T}Q$对任意的$Q$都成立，但我们更关注$Q$为方阵时的情况，因为其有逆且由$Q^{T}Q=I\Rightarrow Q^{-1}=Q^T$，我们叫这种column vector为标准正交向量组成且为方阵的矩阵为正交矩阵 orthogonal matrix。

---

注意：标准正交矩阵 orthogonormal matrix不一定是方阵，当它是方阵的时候，我们叫它正交矩阵 orthogonal matrix。

1.2正交矩阵

---

为什么我们如此关注标准正交矩阵 orthogonormal matrix为方阵 的情形？

上一讲我们研究了$A^{T}A$的特性，联系我们之前学习的投影矩阵projection matrix，将向量$b$投影在标准正交矩阵$Q$的列空间中，根据上一讲的公式得$P=Q(Q^{T}Q{)}^{-1}{Q}^T$，由于标准正交矩阵$Q$的性质，易得$P=Q{Q}^T$。

我们断言，当列向量为标准正交基时，$Q{Q}^T$是投影矩阵。极端情况，假设矩阵是方阵，而其列向量是标准正交的，则其列空间就是整个向量空间，而投影整个空间的投影矩阵就是单位矩阵，此时$Q{Q}^T=I$。

投影矩阵的两个性质：

1. $(Q{Q}^T{)}^T=Q{Q}^T$，
   证明：$(Q{Q}^T{)}^T=(Q^T{)}^T{Q}^T=Q{Q}^T$

2.$(Q{Q}^T{)}^2=Q{Q}^T$
证明：$(Q{Q}^T{)}^2=Q{Q}^{T}Q{Q}^T=Q(Q^{T}Q)Q^T=Q{Q}^T$

$我们计算的A^{T}A\hat{x}=A^{T}b$，现在变为$Q^{T}Q\hat{x}=Q^{T}b$，也就是$\hat{x}=Q^{T}b$，分解开来看就是 $\underline{{\hat{x}}_i=q_i^{T}b}$，这个式子在很多数学领域都有重要作用。当我们知道标准正交基，则解向量第$i$个分量为基的第$i$个分量乘以b，在第$i$个基方向上的投影就等于q_i^Tb。}$

##2. Gram-Schmidt正交化法

这是一种将矩阵转化为标准正交向量orthogonormal matrix的方法。按老师的说法Schmidt教我们如何将一个向量标准化normalized，而Graham教我们如何使得各个向量正交orthogonal。

总思路：
已知相互无关的向量$a$,$b$，目标要将$a$,$b$ 变成相互正交且长度为$1 $的$q_1$,$q_2$，可将向量$a$ 固定，然后$b$投影到$a $上，误差$e=B$.

我们有两个线性无关的向量$a,b$，先把它们化为单位正交向量$A,B$：

• 我们取定$a$向量的方向，$a=A$；
• 接下来将$b$投影在$A$的法方向上得到$B$，也就是求子空间投影一讲中，我们提到的误差向量$e=b-p$，即$B=b-\frac{A^{T}b}{A^{T}A}A$。检验一下$A\perp B$，$A^{T}B=A^{T}b-A^T\frac{A^{T}b}{A^{T}A}A=A^{T}b-\frac{A^{T}A}{A^{T}A}{A}^{T}b=0$。（$\frac{A^{T}b}{A^{T}A}A$就是$A\hat{x}=p$）；
• 再将它们单位化，变为单位正交向量$q_1=\frac{A}{\Vert A\Vert },q_2=\frac{B}{\Vert B\Vert }$。

如果我们有三个线性无关的向量$a,b,c$，则我们现需要求它们变换成单位正交向量$A,B,C$：

• 前两个向量我们已经得到了，我们现在需要求第三个向量同时正交于$A,B$；
• 我们依然沿用上面的方法，从$c$中减去其在$A,B$上的分量，得到正交与$A,B$的$C$：$C=c-\frac{A^{T}c}{A^{T}A}A-\frac{B^{T}c}{B^{T}B}B$；
• 再将它们单位化，变为单位正交向量$q_1=\frac{A}{\Vert A\Vert },q_2=\frac{B}{\Vert B\Vert },q_3=\frac{C}{\Vert C\Vert }$。

例子：
现在我们试验一下推导出来的公式，$a=\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right],b=\left[\begin{array}{c}1\\ 0\\ 2\end{array}\right]$：
则$A=a=\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right]$；
根据公式有$B=a-hA$，$h$是比值$\frac{A^{T}b}{A^{T}A}=\frac{3}{3}$，则$B=\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right]-\frac{3}{3}\left[\begin{array}{c}1\\ 0\\ 2\end{array}\right]=\left[\begin{array}{c}0\\ -1\\ 1\end{array}\right]$。验证一下正交性有$A\cdot B=0$。
单位化，$q_1=\frac{1}{\sqrt{3}}\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right],q_2=\frac{1}{\sqrt{2}}\left[\begin{array}{c}1\\ 0\\ 2\end{array}\right]$，则标准正交矩阵为$Q=\left[\begin{array}{cc}\frac{1}{\sqrt{3}}& 0\\ \frac{1}{\sqrt{3}}& -\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{3}}& \frac{1}{\sqrt{2}}\end{array}\right]$，对比原来的矩阵$D=\left[\begin{array}{cc}1& 1\\ 1& 0\\ 1& 2\end{array}\right]$，有$D,Q$的列空间是相同的，我们只是将原来的基标准正交化了。

##3.QR分解

---

我们曾经用矩阵的眼光审视消元法，有$A=LU$。同样的，我们也用矩阵表达标准正交化，$A=QR$，这里的$R$是一个上三角矩阵upper triangular matrix 。

设矩阵$A$有两个列向量$\left[a_1{a}_2\right]$，则标准正交化后有$\left[a_1{a}_2\right]=\left[q_1{q}_2\right]\left[\begin{array}{cc}{a}_1^T{q}_1& a_2^T{q}_1\\ a_1^T{q}_2& a_2^T{q}_2\end{array}\right]$，而左下角的$a_1^T{q}_2$始终为$0$，因为Gram-Schmidt正交化总是使得$a_1\perp q_2$，后来构造的向量总是正交于先前的向量。所以这个$R$矩阵是一个上三角矩阵。

##4.总结

---

1.标准正交基与正交矩阵；
2.Gram-Schmidt正交标准化；
3.QR分解（与LU分解的区别）。

---

#第十八讲：行列式及其性质

---

• 行列式最早是应用在用来判断方程组是否有解，在矩阵被发明后，行列式就拥有了更多的性质和应用。其强大之处在于将整个矩阵的信息压缩到了一个值当中。
• 行列式的英文名为determinant：决定因素，因为他可以决定方程组是否有解即矩阵是否可逆，从另外一个角度来理解，行列式代表了这个矩阵的特征，这是学习特征分解的前置概念。
  ##1.基础性质

---

本讲我们讨论出行列式（determinant）的性质：

行列式的基本性质：
性质1： $\det I=1，单位矩阵行列式值为一。$
性质2：$交换行，行列式变号。$
性质3： a. $\left|\begin{array}{cc}ta& tb\\ tc& td\end{array}\right|=t\left|\begin{array}{cc}a& b\\ c& d\end{array}\right|。$
b. $\left|\begin{array}{cc}a+a^{\prime }& b+b^{\prime }\\ c& d\end{array}\right|=\left|\begin{array}{cc}a& b\\ c& d\end{array}\right|+\left|\begin{array}{cc}{a}^{\prime }& b^{\prime }\\ c& d\end{array}\right|。$

由性质1和2可知，对置换矩阵有$\det P=\{\begin{array}{ll}1& even\\ -1& odd\end{array}$。
举例：$\left|\begin{array}{cc}1& 0\\ 0& 1\end{array}\right|=1,\left|\begin{array}{cc}0& 1\\ 1& 0\end{array}\right|=-1$，于是我们猜想，对于二阶方阵，行列式的计算公式为$\left|\begin{array}{cc}a& b\\ c& d\end{array}\right|=ad-bc$。

性质3(b)对于每行都单独成立，其他行则不变，即不能同时组合第一行和第二行。$det(A+B)≠det(A)+det(B) $。

2. 推导出的性质

---

更多的性质可以从以上的三条性质中推导出来。

性质4：$如果两行相等，则行列式为零。使用性质2交换两行易证。$

**性质5 **：$从第k行中减去第i行的l倍，行列式不变。$
解析：这条性质是针对消元的，我们可以先消元，将方阵变为上三角形式后再计算行列式。
举例：$\left|\begin{array}{cc}a& b\\ c-la& d-lb\end{array}\right|\stackrel{3.b}{=}\left|\begin{array}{cc}a& b\\ c& d\end{array}\right|+\left|\begin{array}{cc}a& b\\ -la& -lb\end{array}\right|\stackrel{3.a}{=}\left|\begin{array}{cc}a& b\\ c& d\end{array}\right|-l\left|\begin{array}{cc}a& b\\ a& b\end{array}\right|\stackrel{4}{=}\left|\begin{array}{cc}a& b\\ c& d\end{array}\right|$

性质6：$如果方阵的某一行为零，则其行列式值为零。$
证明：使用性质3（a）对为零行乘以不为零系数$l$，使$l\det A=\det A$即可证明；或使用性质5将某行加到为零行，使存在两行相等后使用性质4即可证明。
性质7：$有上三角行列式U=\left|\begin{array}{cccc}{d}_1& \ast & \cdots & \ast \\ 0& d_2& \cdots & \ast \\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & d_n\end{array}\right|，则\det U=d_1{d}_2\cdots d_n。$
证明：使用性质5，从最后一行开始，将对角元素上方的$\ast$元素依次变为零，可以得到型为$D=\left|\begin{array}{cccc}{d}_1& 0& \cdots & 0\\ 0& d_2& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & d_n\end{array}\right|$的对角行列式，再使用性质3将对角元素提出得到$d_n{d}_{n-1}\cdots d_1\left|\begin{array}{cccc}1& 0& \cdots & 0\\ 0& 1& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & 1\end{array}\right|$，得证。
性质8：$当矩阵A为奇异矩阵时，\det A=0；当且仅当A可逆时，有\det A\ne 0$。
证明：如果矩阵可逆，则化简为上三角形式后各行都含有主元，行列式即为主元乘积；如果矩阵奇异，则化简为上三角形式时会出现全零行，行列式为零。
再回顾二阶情况：$\left|\begin{array}{cc}a& b\\ c& d\end{array}\right|\stackrel{消元}{}\left|\begin{array}{cc}a& b\\ 0& d-\frac{c}{a}b\end{array}\right|=ad-bc$，前面的猜想得到证实。

性质9：$\det AB=(\det A)(\det B)$。
解析：使用这一性质，$\det I=\det A^{-1}A=\det A^{-1}\det A$，所以$\det A^{-1}=\frac{1}{\det A}$。
同时还可以得到：$\det A^2=(\det A{)}^2$，以及$\det 2A=2^n\det A$，这个式子就像是求体积，对三维物体有每边翻倍则体积变为原来的八倍。

性质10：$\det A^T=\det A。$
$前面一直在关注行的属性给行列式带来的变化，有了这条性质，行的属性同样适用于列，比如对性质2就有“交换列行列式变号”。$
证明：$\left|A^T\right|=\left|A\right|\to \left|U^T{L}^T\right|=\left|LU\right|\to \left|U^T\right|\left|L^T\right|=\left|L\right|\left|U\right|$，值得注意的是，$L,U$的行列式并不因为转置而改变，得证。