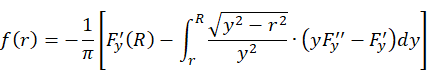Abel逆变换的MATLAB实现(未完成版)
绪论
Abel逆变换常用于对于三维物体的重建中。Abel变换(Abel Transform)的意义为一个轴对称函数到向一个平面的投影,而Abel逆变换则是通过投影反演出原轴对称函数。其实际意义在于对某些轴对称的光源进行记录时可以通过平面记录器件还原出原有光源光强的三维分布,对于医学重建、火焰重建等有重要意义。
研究现状
Abel逆变换是一个典型的不适定问题,也就是说微小的数据误差在经过算法处理后,最终还原结果往往会出现巨大误差。这可以从Abel逆变换的定义式上理解一二。Abel逆变换定义式如下(摘自Wikipedia)
这个式子表示对于函数F进行Abel逆变换求得函数f(r)。同时在实际实验中,由于记录条件的限制,F往往是离散的,上式需要写成离散的格式,如下
其中上标从无穷变为n,是因为现实中的研究对象往往可认为在一定范围内,超出该范围则F值为0,这里将n看作这个范围,可以理解成CCD相机上该列值不为0的像素数目。可以看到其中存在对于F的差分运算,直接反演将产生可观的误差,且误差会被求和运算累积到无法接收的程度。因此Abel逆变换存在许多数值解法,包括:积分算子法、离散正则化方法、三次样条函数法、傅里叶-汉克尔变换方法和基函数展开(BASEX)法。在接下来的内容中,博主会对这些方法的基本思路进行介绍,尽量总结各自特点,并挑选其中较为常用的方法,给出其算法实现。
基本思路与特点
在阅读几篇文献后,对于以上数值解法有了一些了解,对其基本思路进行总结,并提出对于其特点(优缺点)的一些个人见解。对于算法的介绍按照我认为比较容易接收的逻辑进行。
三次样条函数法(插值\拟合方法)
由Abel变换的定义式可知,如果能得到像函数F的导数,则只需要进行简单的积分(求和)计算即可得到最终的结果。但是实际测量中像函数往往是离散值,因此导出了定义式的离散格式,其中微分运算用差分运算代替了,无疑带来了更大的误差。那么能否利用已知的离散像函数点还原出连续的像函数再进行求导呢?通过已知离散点还原连续函数,我们自然想到了插值或者拟合的方法,在文献[1]中给出了三次样条插值法和离散数据曲线拟合法就是基于这种思路。其中三次样条插值法实现方法较为简单,但是两种误差非但未考虑测量误差,还会引入额外的误差,因此仅介绍我认为理解较为简单的三次样条函数法。
首先对所有点进行分段,每一段中取合适的点数,完成三次样条函数插值,之后带入逆变换定义式即可。三次样条插值的好处在于保证了分段插值各点函数的连续性,使得导数的计算更为简洁。同时算法十分简单清晰,三次样条插值是十分常用的函数插值方法,十分成熟。但是所有的插值与拟合方法都未考虑测量本身的误差,因此实际上并没有很好的解决逆变换的病态性,这是这种方法最大的缺点。
积分算子法
积分算子法处理Abel逆变换的出发点有两个。一是解决积分奇异性的问题(在y=r时被积函数取值趋于无穷);二是考虑测量时的误差条件。其基本思路是首先对Abel逆变换的定义式进行分部积分处理,得
此时积分中的奇异性被消除了,但增加了二次微分。之后通过积分算子方法求得微分的稳定近似,再用复化梯形积分公式进行数值积分,得到f(r)的稳定近似。其中积分算子方法包括定义积分算子以及函数函数延拓,最终保证误差水平在测量误差水平的开方量级。而由于实际中是离散值,因此我认为复化梯形积分公式可以省略,在算得F的一阶与二阶导数的前提下仅采用离散的求和计算即可。具体的积分算子方法过程见文献[2]、[3]。
这种方法的优点在于其对于方法的误差水平给出了具体的衡量,保证了实验的精度。同时方法消除了积分的奇异性,使程序实现与算法本身更为贴近。但是方法的缺点在于其对于数学水平的要求较高(超出了博主的耐心),而且定义积分算子的文章中,见文献[2][3],所研究的Abel变换和我们所说的,也是实际中用到的存在一定的差别,如何推广过来并保证正确性对于数学基础提出了更高的要求。
离散正则化方法
专门讨论离散正则化方法的文献[4]说实话博主不是很看懂(如果有理解的欢迎讨论),因为其中涉及的数学专业名词有一些博主很陌生,理解过于抽象,程序实现中十分不便利,因此着重于公式部分。博主注意到文献[4]、文献[5]中都有将Tikhonov的正则化思想作为讨论基础,因此将之归为一类,并对文献[5]的方法进行重点讨论。因为博主感觉文献[5]的思路较文献[4]更贴近实际,便于算法的实现。
离散正则化,顾名思义,分为两个步骤——离散和正则化。首先是问题的离散处理。在离散形式中Abel变换对应一个投影矩阵
对应于A,原函数f可写作n维列向量,投影函数F可写作m维行向量。这里m于n的关系与投影方式有关,如果是点光源投影,则m与n大小与光源到物体距离和物体到接受面的距离相关;如果是平行光投影,则m=n。这里我们考虑较为简单的m=n的情况。此时Abel变换的离散形式可写作矩阵表达式如下
这是一个病态的问题。当求解向量f时,即使向量F仅产生微小的振荡,都会造成向量f的大幅度变化。由Tikhonov的研究可知,求解反问题的正则化方法等价于寻找如下形式能量泛函的最优解:
其中R(f)是限定解范围的正则项,后面的二阶范数是数据保真项,正则项前的参数是平衡这两者的正则化参数。在文献[5]中,为了能够还原既有平滑区域,又有间断的原函数,其通过自适应系数w将TV(全变分,total variation)正则项和二阶正则项相结合,提出了ADAP(adaptive)模型,此时能量泛函为:
其中w是一个n*n的对角矩阵,其对角元为:
这个算法的思路是通过自适应系数调节,在较平滑区域自适应系数w较小,二阶正则项起主要作用;在间断区域自适应系数w较大,TV正则项其主要作用。这个算法的优点在于基于Tikhonov的研究,保证了数值的稳定,同时结合了TV正则项和二阶正则项的优势,可以很好的保证对于平滑和间断区域的还原,不会产生阶梯效应。但是这个算法的缺点在于算法本身较为复杂,在之后的部分博主会介绍算法的具体实现,其中涉及两个迭代,计算量和计算时间也略长。
基函数展开法
基函数展开法的基本思路是认为原函数可以展开为一系列高斯型基函数的加权求和形式,而像函数可以转换为这些基函数经Abel正变换得到的基转换函数的加权求和形式,且二者的权重是不会改变的。因此可以先将利用像函数和基转换函数求出权重,进而根据权重和基函数求出原函数。
这种方法的优点在于其思路异于理解,实现(在后续会给出)也很清晰,是通过矩阵形式实现,可以直接从离散数据进行反演,经过文献[6]中的数值仿真实验验证,其可以很好地反演有噪声的像函数。但是这个方法的缺点在于缺少其抑制噪声的理论证明,只给出理论仿真验证难免让人怀疑其实用性。
但是基于基函数展开的方法无疑带给人启发,让人思考能否通过其他的变换的结合以实现Abel逆变换。文献[7]论证了Abel逆变换可以转换为汉克耳变换和傅里叶变换的结合,从而通过MATLAB简便的实现,具体关系式如下:
同时这种方法的降噪措施也非常简便易懂,仅需要在进行傅里叶变换后对频谱信号进行维纳(Wienner)滤波即可。本方法的缺点在于维纳滤波器构建时需要知道噪声的功率谱密度,尽管我们可以假设噪声是白噪声,这也确实符合大多数实际情况,但实际上我们仍然无法知道噪声的实际功率谱密度,甚至有可能其并不为白噪声。
算法实现
在这个部分,博主主要介绍积分算子法、正则项将TV正则项和二次正则项自适应结合的离散正则化方法及傅里叶变换和汉克耳变换结合的基函数展开法这三种考虑测量误差的方法。
积分算子法
根据上一部分所说的内容,积分算子法的重点在于已知像函数的误差水平,求解其一阶与二阶导数的稳定近似。假设带有扰动的像函数误差水平表达如下式:
![]()
这种假设对应的实际意义在于其对应实验中的误差限,这往往是一个已知参数。之后则需要对于积分算子进行确认,这里博主还没有完全理解,有待未来补全。
离散正则化方法
之前已经介绍过,离散正则化方法求解原函数f(r)等价于求解使得能量泛函
最小的f(r)。文献[5]采用增广拉格朗日方法进行求解,算法思路如下:
首先在引入辅助变量的帮助下定义增广拉格朗日函数如下:
参考文献(只提供作者和篇名,懒得写那么正规了)
[1]绍华,朱丹平,吴毅雄. Abel逆变换的数值算法
[2]吕小红,吴传生. Abel变换数值反演的积分算子方法
[3]杨素华,罗兴钧,邱修峰. 求Abel型积分方程数值解的正则化方法
[4]肖庭延,宋金来. Abel变换数值反演的离散正则化方法
[5]杜建鹏,梁海霞,魏素花. 基于Abel变换的图像重建自适应方法
[6]牛春洋,齐宏,王大林,阮立明. 基于Abel变换反演圆柱介质内红外辐射强度
[7]江少恩,刘忠礼,唐道源,郑志坚. 基于快速傅里叶变换和汉克耳变换的逆阿贝尔变换