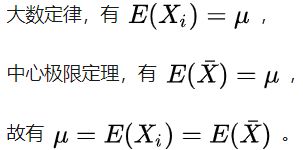机器学习入门-第二天

1，正则化-缓解过拟合

补充: H是对应不同w,b参数的函数f的集合。Ω(f)一般是关于w,b的函数，它的值越小，意味着函数越简单或越平滑。

1. 正则化一般就是在损失函数中加一个惩罚项Ω(f)，这个惩罚项Ω(f)一般是关于w的范数，因为只有w影响函数平滑程度，b只是关于函数的上下移动。
2. 范数：
   

L0范数仅仅表示向量中非0元素的个数, L1范数等于向量中所有元素绝对值之和, L2范数表示向量（或矩阵）的元素平方和。

L1范数可以进行特征选择，即让特征的系数变为0.

L1会趋向于产生少量的特征，而其他的特征都是0，而L2会选择更多的特征，这些特征都会接近于0。

L2范数可以防止过拟合，提升模型的泛化能力，有助于处理 condition number不好下的矩阵(数据变化很小矩阵求解后结果变化很大)（核心：L2对大数，对outlier离群点更敏感！）

下降速度：最小化权值参数L1比L2变化的快

模型空间的限制：L1会产生稀疏 L2不会。

正则化就是在损失函数上加上一个与w（斜率）相关的值，那么要是loss function越小的话，w也会越小，w越小就使function更加平滑（function没那么大跳跃）

L1、L2 正则化就只是在这个误差公式后面多加了一个东西, 让误差不仅仅取决于拟合数据拟合的好坏, 而且取决于参数的值的大小. 如果加的是每个参数的平方, 那么我们称它为 L2正规化, 如果是每个参数的绝对值, 我们称为 L1 正规化. 

我们拿 L2正规化来探讨一下, 机器学习的过程是一个 通过修改参数 θ来减小误差的过程, 可是在减小误差的时候非线性越强的参数, 比如在 x^3 旁边的θ4 就会被修改得越多, 因为如果使用非线性强的参数就能使方程更加曲折, 也就能更好的拟合上那些分布的数据点. 但这样可能会导致过拟合,因此需要加上正则项惩罚.

参考:L1 / L2 正规化 (Regularization)https://morvanzhou.github.io/tutorials/machine-learning/ML-intro/3-09-l1l2regularization/

• L2 regularizer ：使得模型的解偏向于范数较小的 W，通过限制 W 范数的大小实现了对模型空间的限制，从而在一定程度上避免了 overfitting 。不过 ridge regression 并不具有产生稀疏解的能力，得到的系数仍然需要数据中的所有特征才能计算预测结果，从计算量上来说并没有得到改观。
• L1 regularizer ：它的优良性质是能产生稀疏性，导致 W 中许多项变成零。 稀疏的解除了计算量上的好处之外，更重要的是更具有“可解释性”。

       问：为什么通过L1正则、L2正则能够防止过拟合

　　答：过拟合产生的原因通常是因为参数比较大导致的，通过添加正则项，假设某个参数比较大，目标函数加上正则项后，也就会变大，因此该参数就不是最优解了。

　　问：为什么过拟合产生的原因是参数比较大导致的？

　　答：过拟合，就是拟合函数需要顾忌每一个点，当存在噪声的时候，原本平滑的拟合曲线会变得波动很大。在某些很小的区间里，函数值的变化很剧烈，这就意味着函数在某些小区间里的导数值（绝对值）非常大，由于自变量值可大可小，所以只有系数足够大，才能保证导数值很大。

2，无偏估计，大数定律，中心极限定理

• 数学期望

• 中心极限定理

样本的平均值约等于总体的平均值。不管总体是什么分布，任意一个总体的样本平均值都会围绕在总体的整体平均值周围，并且呈正态分布。

• 大数定律

同分布则期望和方差一样，密度函数和分布函数也一样。每一个单独样本和总体样本都是同分布，因此单独样本的期望等于总体样本的期望。

• 理论基础

参考：https://www.matongxue.com/madocs/607.html 如何理解有偏估计量，方差估计的偏差

 

参考：

李宏毅机器学习笔记2  https://www.cnblogs.com/xxlad/p/11201463.html

如何通俗易懂地解释「范数」？https://zhuanlan.zhihu.com/p/26884695  

对于正则化的理解            https://www.cnblogs.com/pinking/p/9310728.html

L1范数与L2范数的区别     https://blog.csdn.net/rocling/article/details/90290576