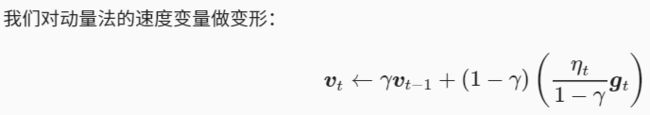机器学习入门-第三天

优化算法

1,自适应梯度下降Adagrad

1,牛顿法

并不是所有的方程都有求根公式，或者求根公式很复杂，导致求解困难。利用牛顿法，可以迭代求解。原理是利用泰勒公式，在x0处展开，且展开到一阶，即f(x) = f(x0)+(x－x0)f'(x0)

求解方程f(x)=0，即f(x0)+(x-x0)*f'(x0)=0，求解x = x1=x0－f(x0)/f'(x0)，因为这是利用泰勒公式的一阶展开，f(x) = f(x0)+(x－x0)f'(x0)处并不是完全相等，而是近似相等，这里求得的x1并不能让f(x）=0，只能说f(x1)的值比f(x0)更接近f(x）=0，于是乎，迭代求解的想法就很自然了，可以进而推出x(n+1)=x(n)－f(x(n))/f'(x(n))，通过迭代，这个式子必然在f（x*）=0的时候收敛。

当然如果使用泰勒二阶展开,那么得到结果就更精确.

2, 怎样自适应

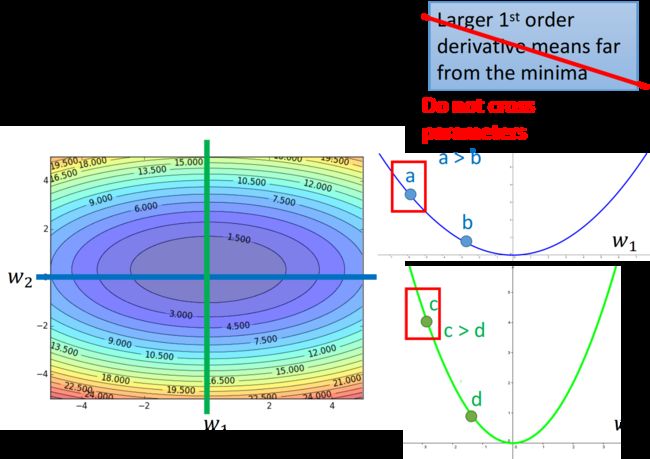
3,梯度(一次导数)越大,并不意味着距离最低点越近,因此学习率的的变化不能只考虑梯度.

在有多个参数的情况下: w1和w2分别是loss function的两个参数，分别在w2和w1处画出梯度曲线，可以看出，比起a点，c点距离最低点更近，但是它的gradient却越大. 因此,绿色曲线的曲率大一点，即二次导数更大，所以虽然c的梯度(一次导数)比较大，但是由于二次导数也大，综合影响c点离最低点比较近，给一个小一点的学习率就可以了.

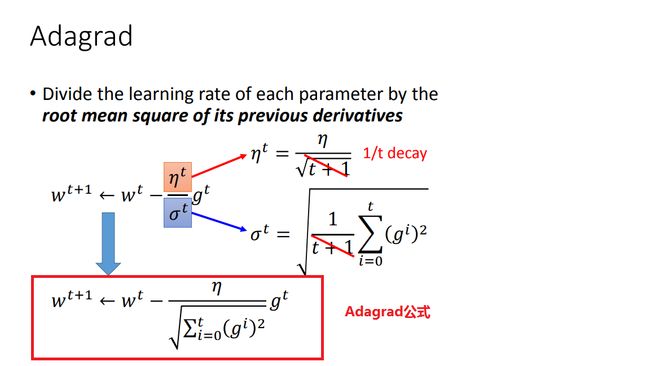
4,为什么Adagrad用梯度的平方和开根号作为分母,而不直接用二阶导数?

因为曲线越宽，曲率越小，很多梯度的平方和就越小，因此二次微分就越小,可以约等于梯度平方和开根,其次,计算二阶导数比较复杂.

2,动量梯度下降SGDM

避免大幅度的徘徊着向最低点前进.

参考:

https://blog.csdn.net/BVL10101111/article/details/72615621

https://blog.csdn.net/tsyccnh/article/details/76270707

https://blog.csdn.net/nanhuaibeian/article/details/100836439

指数加权平均中的指数表示各个元素所占权重呈指数分布。

 

动量考虑了历史的梯度，要是当前时刻的梯度与历史时刻梯度方向相似，这种趋势在当前时刻则会加强；要是不同，则当前时刻的梯度方向减弱。说白了就是求合向量的过程,以下图片演示了梯度加动量后的合向量.

动量梯度下降更新公式:

λ为衰减率,其表示之前梯度对当前的影响,其值越大,影响越大

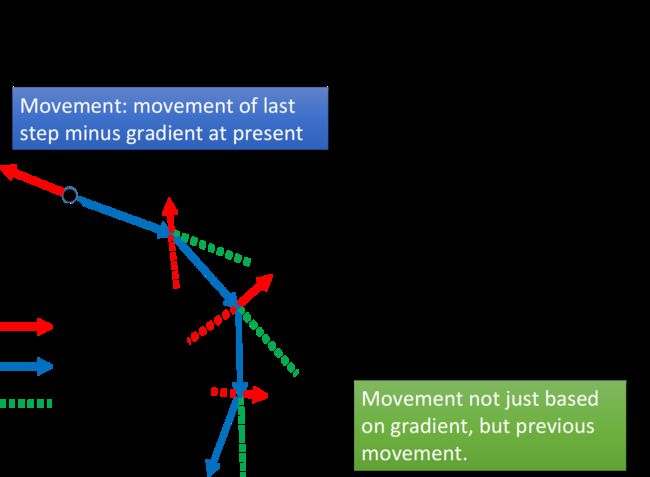
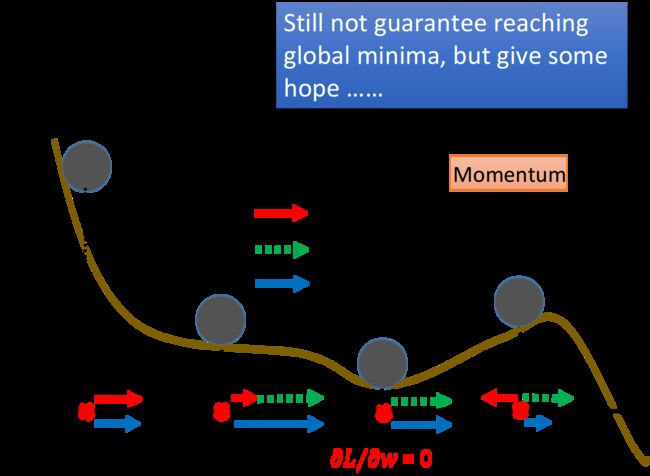
注意下图红色虚线和绿色虚线的合向量才是最后的移动方向:gradient告诉我们走红色虚线的方向，惯性告诉我们走绿色虚线的方向，合起来就是走蓝色的方向. λ会告诉你惯性(上一步的movement)的影响是多大.

在加入Momentum以后，每一次移动的方向，就是negative的gradient加上Momentum建议我们要走的方向，Momentum其实就是上一个时间点的movement

下图中，红色实线是gradient建议我们走的方向，直观上看就是根据坡度要走的方向；绿色虚线是Momentum建议我们走的方向，实际上就是上一次移动的方向；蓝色实线则是最终真正走的方向. 如果我们今天走到local minimum的地方，此时gradient是0，红色箭头没有指向，它就会告诉你就停在这里吧，但是Momentum也就是绿色箭头，它指向右侧就是告诉你之前是要走向右边的，所以你仍然应该要继续往右走，所以最后你参数update的方向仍然会继续向右；你甚至可以期待Momentum比较强，惯性的力量可以支撑着你走出这个谷底，去到loss更低的地方.

 

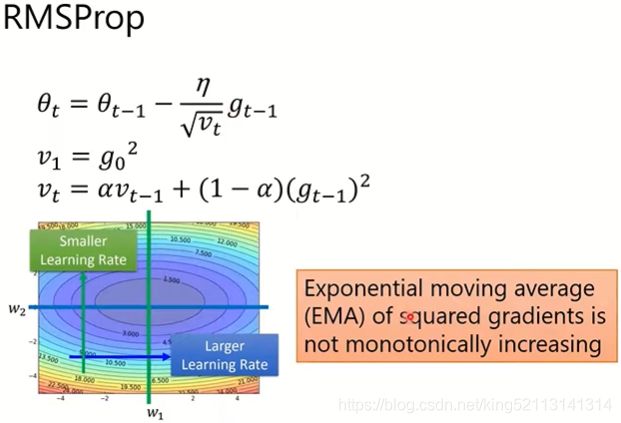
3,RMSprop算法:

参考:https://sakura-gh.github.io/ML-notes/ML-notes-html/13_Tips-for-Deep-Learning.html

Adagrad的分母是对过程中所有的gradient取平方和开根号，这是一个累加过程,也即分母一直在增大，所以学习率在迭代过程中一直在降低（或不变）。因此，当学习率在迭代早期降得较快(初始gradient之和比较大)且当前解依然不佳时，AdaGrad算法在迭代后期由于学习率过小，可能较难且花费较长时间找到一个有用的解。

RMSprop既有动量梯度下降的合向量减小摆动幅度加速收敛的优点,同时衰减率的引入也会逐步降低过去的历史梯度的影响,使得学习率在迭代过程中就不再一直降低（或不变）.

4, Adam

ϵ是为了维持数值稳定性而添加的常数，如10^-8，并避免除数变为0。

由于m0/v0初始化为0，会导致mt/vt偏向于0，尤其在训练初期阶段，梯度权值之和比较小，需要将权值之和修正为1, 所以，此处需要对梯度均值mt/vt进行偏差纠正，降低偏差对训练初期的影响。

adam参考:

如何理解Adam算法-薰风初入弦https://www.zhihu.com/question/323747423/answer/790457991

https://cs231n.github.io/neural-networks-3/

http://zh.gluon.ai/chapter_optimization/adam.html

常用优化算法https://blog.csdn.net/weixin_41786536/article/details/100187562

深度学习中的优化算法串讲https://www.jianshu.com/p/c7fafdb729f1

深度学习中的优化算法总结https://www.cnblogs.com/zingp/p/11352012.html

Adam优化器https://www.jianshu.com/p/f034efd799dd

参考:

以下链接都是关于adagrad:

https://sakura-gh.github.io/ML-notes/ML-notes-html/5_Gradient-Descent.html

https://www.cnblogs.com/xxlad/p/11283104.html

https://zhuanlan.zhihu.com/p/122565620

https://github.com/datawhalechina/leeml-notes

牛顿法直观理解https://blog.csdn.net/qq_36330643/article/details/78003952

优化算法——牛顿法https://blog.csdn.net/google19890102/article/details/41087931