三维重建（四）PMVS算法 the patch-based MVS algorithm

通过前面的介绍，已经获得了相机的参数，我们可以利用这些参数使用基于面片的三维多视角立体视觉算法（PMVS）重建出稠密的点云。下面详细介绍一下PMVS算法。

一、基本概念介绍

1、面片（patch）

面片 p 是一个近似的正切与重建物体表面的一个小矩形，他的一边平行于参考相机的x轴。对于一个面片 p ，他的几何特征如下：
中心点： c(p) ；
单位法向： n(p) ，该向量指向相机的光心；
面片 p 对应一个参考图像 R(p) ，在 R(p) 中 p 是可见的。针对 p 有扩展矩形， p 在 R(p) 中的投影是 μ×μ 大小的，在原论文中 μ= 5 or 7

2、灰度一致性函数（Photometric Discrepancy Function）

首先，我们另图像集合 V(p) 是所有在自身图像中可见面片 p 的图像集合（显然这里有 R(p)∈V(p) ，将在后面介绍 V(p) 的获得已经 R(p) 的确定）那么，灰度一致性函数定义如下：

g(p)=1|V(p)−R(p)|∑I∈(V(p)−R(p))h(p,I,R(p)

在这里， V(p)−R(p) 是指出去 R(p) 的 V(p) 的其他元素； h(p,I1,I2) 是指 I和R(p) 的灰度一致性函数，计算过程如下：
1. 首先把面片 p 划分为 μ×μ 的小格；
2. 通过双线性差值的方法，对 p 在 Ii 的图像上的投影进行差值，得到像素灰度 q(p,Ii) ；
3. 用1减去 q(p,I1) 和 q(p,I1) 的NCC(normalized cross correlation)值。
过程如下图所示：

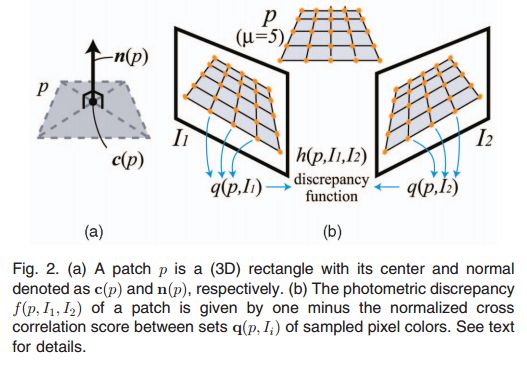
由于 g(p) 对于图像中出现高光或者有障碍物的情况下的效果不好，因此在实际情况下，我们需要保证图像 I 和图像 R(p) 的灰度一致性函数大于一定的值 α （后面将会介绍如何选择这个阈值）。因此有：

V∗(p)=I|I∈V(p),h(p,I,R(p)≤α)

g∗(p)=1|V∗(p)−R(p)|∑I∈(V∗(p)−R(p))h(p,I,R(p)

3、面片的优化

面片优化的目的就是恢复那些 g∗(p) 较小的面片，每个面片的重建过程分为以下两步：
4. 初始化面片的相关参数 c(p),n(p),V∗(p)和R(p) ；
5. 优化 c(p)和n(p)
这里的第一步初始化的过程在后面用到，这里先讲以下 c(p)和n(p) 的优化。几何参数 c(p)和n(p) 的优化是通过最小化 g∗(p) 而得到的。为了简化计算，将 c(p) 约束在某一条光线上，这样 p 在其对应的可视图集 V∗(p) 中某个图像的投影位置就不会变，因此降低了 p 的自由度。 n(p) 是由欧拉角（yaw and pitch）决定的，可以用共轭梯度法求解这个优化问题。（这一段我没有懂这些方法）

4、图像模型

基于面片的物体表面的表示的优势是他的灵活性，然而却不容易找到面片的连续性。为了解决这个问题进行了如下的操作，把图像 Ii 分成了许多 β1×β1 像素的的小块 Ci(x,y) ，这里 x,y 表示图像块的下标， i 表示这是第 i 张图像的。给定一个面片 p 和对应的 V(p) ，把p投影到 V(p) 的图像中，以得到面片p对应的图像块，每个图像块 Ci(x,y) 用一个集合 Qi(x,y) 记录了所有投影到这个图像块的面片。同理，我们用 Q∗i(x,y) 来表示用 V∗(p) 得到的结果。如下图所示：

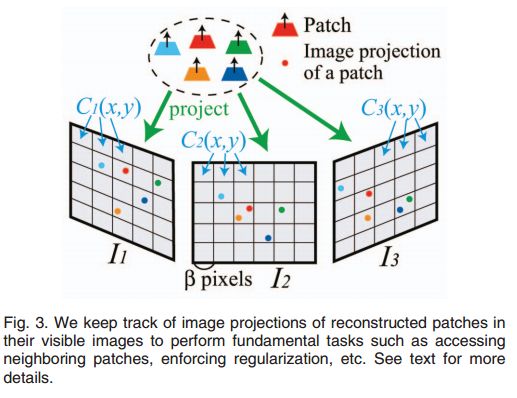
二、面片的重构

基于面片的多视角三维立体视觉算法的目的就是保证在每个图像块 Ci(x,y) 上至少有一个面片的的投影。主要分为以下三步：
1. 初始化特征匹配（initial feature matching）；
2. 面片生成（patch expansion）；
3. 面片筛选（patch filtering）；
初始化特征匹配的目的就是生成一系列稀疏的面片，面片的生成和筛选都要执行n次使得面片足够稠密，同时去除不好的面片。下面依次进行介绍。

1、初始化特征匹配

首先用DOG和Harris来提取图像的角点特征，即为每幅图像的特征点。对于图像 Ii ，以及其对应的光心 O(Ii) ，该图像中的特征点 f ，通过允许有两个像素误差的极线约束找到它在其他图像中的同种类型的特征点 f′ ，构成匹配点对 (f,f′) 。然后用这些匹配点对使用三角化的方法生成一系列三维空间点，然后将这些点按照距离 O(Ii) 从小到大顺序进行排列，然后依次尝试生成面片，直到成功。
尝试生成面片的方法如下所示：首先初始化候选面片的 c(p),n(p)和R(p) ，如下所示：

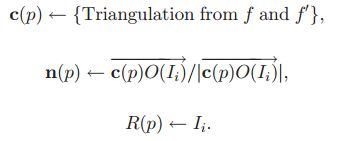
由于生成的面片可能有很多错误的情况，因此我们认为在图像 Ii 中可见的面片是面片的法向量与面片中心到相机光心的连线夹角小于一定角度 α 的图像，即满足：

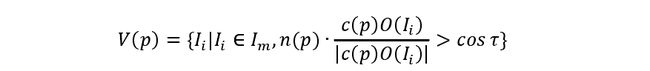
同样 V∗(p) 的获得与前面所讲的方法相同。这样面片的信息都已经初始化过了，然后根据前面所讲的对 c(p)和n(p) 进行优化，并将优化过后的 c(p)和n(p) 带入

V∗(p)=I|I∈V(p),h(p,I,R(p)≤α)

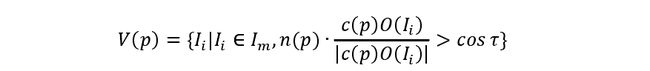中对 V(p)和V∗(p) 进行更新。如果 |V∗(p)|≥r ，集认为面片 p 的可视图像至少为 r 幅，即接受面片 p ，重建成功。并将面片p存储到对应的可视图像的图像块中（即更新 Qi(x,y)和Q∗i(x,y) ）。
具体的算法描述和图示如下图所示，过程就是我上面说的过程，懒得翻译了，很好理解。

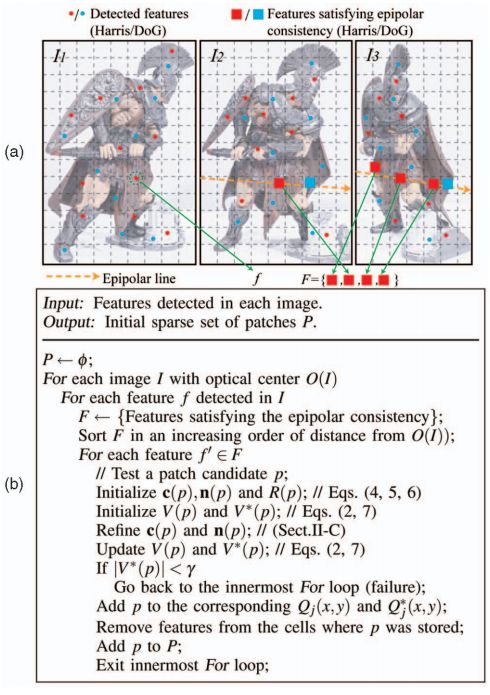
2、面片生成（patch expansion）

面片生成的目的就是保证每个图像块至少对应一个面片。通过上面生成的面片，重复的生成新的面片，具体来说就是给定一个面片 p ，首先获得一个满足一定条件的邻域图像块集合 C(p) ，然后进行面片生成的过程。
下面是面片p的两个相关概念：
图像块邻域 C(p) ：

面片 p 和 p′ 的临近关系：

|(c(p)−c(p′))⋅n(p)|+|(c(p)−c(p′))⋅n(p′)|<2ρ1

即当面片 p 和 p′ 满足上式时，即判定两者为临近关系，上式中的 ρ1 由 R(p) 在 c(p)和c(p′) 中的深度决定。
当存在一个面片 p′ 其所属的图像块 Ci(x′,y′) 满足 Ci(x′,y′)∈C(p) ，同时 p和p′ 属于近邻关系时，此时将 Ci(x′,y′) 从 C(p) 中删除，不对他进行面片生成。同时，即使这个条件没有满足，只要 Qi(x′,y′) 不为空，也不需要再此图像块上执行生成操作。
对于 C(p) 中其余的图像块，将会执行面片生成的操作流程以生成新的面片 p′ 。首先用 p 的相应变量初始化 p′ 的 n(p′)、R(p′)和V(p′)，对于 c(p’)的初始值为穿过 Ci(x,y) 的可视光线与面片 p 所在平面的交点。使用

V∗(p)=I|I∈V(p),h(p,I,R(p)≤α)

由 V(p) 得到 V∗(p′) ，再由上面提到的方法对 c(p′)和n(p′) 进行优化。在优化的过程中，将 c(p′) 约束在一条直线上，使得 p′ 在图像 Ii 上的位置不会改变，始终对应的是 Ci(x,y) 。优化完成后，给 V(p′) 加上一组图像，这些图像块些根据深度测试判断为 p′ 对其应该是可见的，并根据此更新 V∗(p′) 。
最终如果 |V∗(p′)|≥r ，则判定 p′ 是可接受的，即生成成功，同时更新 Qi(x,y) 和 Q∗i(x,y) 。具体的参数设置参见原论文。
面片生成的算法流程如图所示：

3、面片过滤（patch filtering）

在面片的重建过程中，可能会生成一些误差较大的面片，因此需要过滤来确保面片的准确性。
第一个过滤器是通过可视一致性进行过滤，另 U(p) 表示与当前可视信息不连续的面片集合，所谓的不连续就是 p 和 p′ 两个面片不属于近邻关系，但是却存在于同一个 Qi(x,y) 中。对于 U(p) 中的面片 p ，如果满足下列条件，则将其过滤掉。

|V∗(p)|(1−g∗(p))<∑pi∈U(p)1−g∗(p)

直观上来讲，如果 p 是一个异常值，那么 1−g∗(p) 和 |V∗(p)| 都会比较小，这样 p 一般都会被过滤掉。
第二个过滤器同样也是考虑可视一致性，不过会更加严格，对于每个面片 p ，我们计算他通过深度测试得到的可视图像的总数，如果数目小于 r ，那么则认为 p 是异常值，从而过滤掉。
第三个过滤器，对于每个面片 p ，在 V(p) 中，收集这样的一组面片，他们的映射到面片 p 自己所在的图像块以及所有相邻的图像块，如果 p 的八邻域内的面片数量占收集所得面片数量的比例小于0.25，则任务 p 是异常值，将其过滤掉。