双摄与双目视觉

 

越来越多的手机开始上双摄，首先解释一下双摄的目的，双摄可以达到什么样的效果。首先双摄可以分为两类，一类是利用双摄获得图像中物体到镜头或者焦距的距离，得到景深信息就可以进行后续的3D重建、图像分割、背景虚化等；一类是利用两个摄像头所成的不同图像进行图像融合，获得更多的细节信息，包括RGB镜头和Mono黑白摄像头获得图像的融合，黑白摄像头可以捕捉更多的细节，即解析力更高；还有广角摄像头和长焦摄像头所获图像的融合和不同曝光参数的摄像头实现的HDR效果。第一类中为了通过三角定位原理实现景深信息的获得，两个摄像头的物理距离要尽可能大，而在第二类中为了图像融合，两幅或者多幅图像需要进行对准，所以需要两个摄像头尽可能重叠。所以这里有一个需要平衡的点，当然，还是要算法尽可能好。需要说明的是，景深的获得可以通过深度相机主动发射和捕捉射线来直接实现距离的计算。IPhone X就前置了结构光深度相机，采用了伪随机散斑。此外还有飞行时间深度方案(Time of Fly,TOF)，可以绕开结构光的专利问题。这篇先来理解传统的基于小孔成像的三角定位(triangulation)。

立体视觉(stereo vision)狭义上指的就是从两个或者多个摄像头中获得图像的深度信息。它和双目立体视觉和稠密立体算法密切相关。现在研究的重点是实现实时性。

先来看单摄像头的情况。在摄像头轴线的延长线上的多个点所成的像是重合的，所以无法区分它们。这也是造成一些视觉混淆现象的原因，比如下图的哪一栋楼在前面，具体原因可能还有不同人眼的感知不同波长的锥体的分布不同，而分布不同的原因可能又是不同作息规律对锥体的训练情况不同造成的。

 

再看一下双摄像头下的成像。

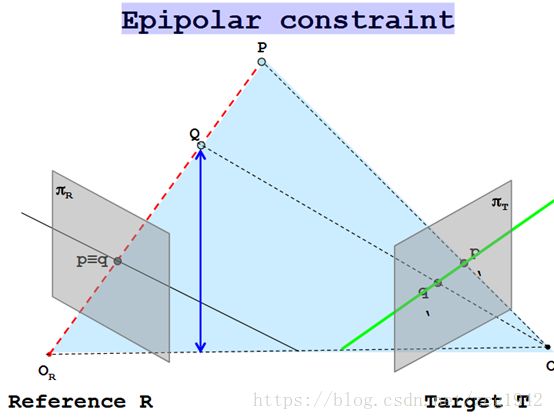
在双摄像头下，总会存在一个摄像头中会由于距离的原因产生差异。先抛去三角定位原理，这里的关键就是如何在两幅图像中计算得到p(q)对应的p’、q’。这里首先要介绍一下极线约束(epipolar constraint)。

曲线L上A、B两点的切线相交于点P，那么P就是极点，直线AB称为极点(Epipole)P的极线。极线约束是一种点对直线的约束，而不是点与点的约束，尽管如此，极线约束给出了对应点重要的约束条件，它将对应点匹配从整幅图像寻找压缩到在一条直线上寻找对应点。直接在两个摄像头所成图像中当然可以通过SIFT特征点等寻找匹配对，但是通过极线约束我们将搜索范围从滑窗的大小缩小到一条直线的范围，对于参考图中的点p，通过极线约束，我们可以找到实际物体P、Q在Target图中的位置所在的直线。

由上图，红色线上的P、Q及其延长线上的点都会被投影在Target T中的绿色线上。在下图中，X、X1、X2、X3在左摄像头中都重叠为同一点，而在右摄像头的视角中，表现为几点共线。

OL和OR是我们模仿小孔成像的小孔，或者理解为相机中的透镜所在的位置。所成的像应该在其后方，且是倒立的像，但为了方面，我们取小孔之前的正立像作为生成的图像，它与实际的倒像呈翻转和缩放的关系。我理解的对极约束的物理意义是获得分别获得两个摄像头相对于另外一个的位置。所以两个极点eL和eR。eL是OR在OL下的投影，eR是OL在OR下的投影。这样，左摄像头就知道了右摄像头的位置，右摄像头也知道了左摄像头的位置，这样就获得了先验知识，有利于对应点的查找和匹配。X、OL、OR三点确定一个平面，这就是epipolar plane极面，即目的物体位置，两个透镜中心确定了极面，这个极面是可变的（极面与透镜中心，目标物体中心有关，极点只与两个镜头位置有关）。对每一个确定的极面，极线就是极面与成像的交线，分别是通过另一个透镜中心的直线在本透镜下的投影。极点和极线是曲线上点和该点的切线的一般化，而三维空间中的极点极线又是对曲线情况的一般化，所以不太好理解，只能通过投影的方法解释。

这里的图示，尤其是左摄像头的图示，只是表示了几个物体的相对位置的重叠遮挡情况。即便不同物体的中心与透镜中心成一条直线，更远的物体往往只有一部分会被前面的物体遮挡。这里成像模型简化为小孔成像，物体也简化成质点，而实际上镜头和物体都是有大小的，实际情况中往往不是因为投影重叠造成无法判断距离远近，实际即便是单摄像头中远近不同的物体也会有不同的成像表现，只不过单摄像头下这种不同差异可能很小，需要依靠个人经验判断甚至难以判断，而且更是无法获得精确的距离大小。

在数学上，我们需要描述左摄像头获得图像中的点和另一幅图像中的极线，这样像素点在右摄像头图像中的对应点一定在这一条直线上（搜索范围可以从2D缩小到1D）。这就涉及到两个矩阵：对极矩阵(Epipolar Matrix)/本质（本征矩阵Essential Matrix）和基本矩阵(Fundamental Matrix)。

本征矩阵描述的是两个相机坐标系之间的关系（旋转R和平移T）。Pl是物体P在Ol相机坐标系中的坐标，Pr是物体P在Or相机坐标系下的坐标。注意，是物体的坐标，而不是图像中像素的坐标。

R是正交矩阵，所以

因为三向量共面， 

所以，本征矩阵E=RS

因为 ，所以本征矩阵只和外参R和T有关，且S的秩rank=2。

本征矩阵只包含了两个摄像头的相对位置。对于具体的图像，不仅与小孔/透镜的位置有关，还与透镜的焦距等有关。透镜的焦距等属于相机的内参。不同相机的内参不同，而且还可能是未知的。我们现在要做的是得到两幅图中对应点的像素的关系。首先可以由目标物体的坐标分别得到其在两幅图像中的坐标。左右两幅图分别有各自的图像坐标系，其关系是偏移量为摄像头的间距Tx（这里考虑的是最简单的摄像头排列情况，更复杂的关系要靠上文提到的本征矩阵来表示）。目标物体的三维坐标同样以左图的原点为原点。

 

xl-xr可得黄色框中Z的表达式。这样就可以得到目标物体到baseline的距离Z。d表示的是两幅图像中的对应点在各自坐标系中的坐标之差xl-xr。f表示镜头的焦距。depth也可以由下图由相似三角形直接得到。需要注意的是绿色的baseline长度是b，且两幅图像（粉色线段）之间的关系也是进行了长度为b的平移。

在本征矩阵中得到了物体在两个镜头坐标系下的坐标的关系，由上图中求图像坐标的表达式也可以得到两幅图中对应点的坐标的关系。也是三个元素的点乘等于0.为了将坐标离散化，将坐标的绝对长度转换成像素点的个数，这才引入了基础矩阵。基础矩阵不仅依赖于两个摄像头之间的平移和旋转量，还依赖于相机的内部参数。

到这里，我们就可以由左图中像素点的坐标得到其在另外一幅图中对应点的约束直线方程。而且通过SVD分解可得极点。

注：

这里的双目视觉是被动的测量，知乎日报的一篇文章讲解了Iphone是如何利用结构光实现了人脸的识别，实现了点与点的配对。

 

Reference：

1.http://vision.deis.unibo.it/~smatt/FBS_GPU.html

2.http://vision.deis.unibo.it/~smatt/Seminars/StereoVision.pdf

3.https://www.cnblogs.com/houkai/p/6661607.html

4.https://zhuanlan.zhihu.com/p/37802103

5.https://blog.csdn.net/lin453701006/article/details/55096777

6.https://blog.csdn.net/KYJL888/article/details/81566961

7.https://www.cnblogs.com/houkai/p/6661607.html

8.http://www.robots.ox.ac.uk/~vgg/hzbook/hzbook2/HZepipolar.pdf