图论---邻接矩阵
一、图的定义
图是由顶点集合(Vertex)及顶点间的关系集合组成的一种数据结构:Graph=( V, E )
V = {x | x ∈某个数据对象 } 是顶点的有穷非空集合;
E ={ (x, y) | x, y ∈V } 是顶点之间关系的有穷集合,也叫做边(Edge)集合。
注:∈为数学符号,表示属于的意思 。例:x∈y:表示x属于y的意思。
在图中的数据元素通常称为顶点 V 。
注意:
1、二叉树和线性表也符合图的特征。二叉树的所有结点相当于顶点的集合,结点间都存在一定的关系;线性表也是一样,也就是说二叉树和线性表是特殊的图。只不过图比线性表和树更加复杂罢了。
2、在线性表中,数据元素之间仅有线性关系,每个数据元素只有一个直接前驱和一个直接后继;在树形结构中,数据元素之间有着明显的层次关系,并且每一层上的数据元素可能和下一层中多个元素相关,但只能和上一层中的一个元素相关;而在图形结构中,结点之间的关系可以是任意的,图中任意两个数据元素之间都可能相关。
二、基本术语
1、无向边:若顶点 x 和 y 之间的边没有方向,则称该边为无向边(x, y),(x, y) 与 (y,x) 意义相同,表示 x 和 y 之间有连接。
2、无向图:若图中任意两个顶点之间的边均是无向边,则称该图为无向图。
3、有向边:若顶点 x 和 y 之间的边有方向,则称该边为有向边
4、有向图:若图中任意两个顶点之间的边均是有向边,则称该图为有向图。
5、邻接:是两个顶点之间的一种关系。如果图包含(u,v),则称顶点v与顶点u邻接。在无向图中,这也暗示了顶点u也与顶点v邻接。换句话说,在无向图中邻接关系是对称的。
6、关联:是指顶点和边之间的关系。在有向图中,边(u,v)从顶点u开始关联到v,或者相反,从顶点v开始关联到u。在无向图中,边(u,v)与顶点u和v相关联。
7、完全图:每个顶点都与其他顶点相邻接的图。
8、度(Degree)的定义:顶点 v 的度是和 v 相关联的边的数目,记为TD(v)。
a、入度:以 v 为头的边的数目,记为ID(v)
b、出度:以 v 为尾的边的数目,记为OD(v)
TD(v) = ID(v) + OD(v)
E = [TD(v1) + TD(v2) + … + TD(vn)] / 2
E = ID(v1) + ID(v2) + … + ID(vn)
E = OD(v1) + OD(v2) + … + OD(vn)
9、权(Weight)的定义:与图的边相关的数字叫做权,权常用来表示图中顶点间的距离或者耗费。带权的图通常称为网。
10、路径:依次遍历顶点序列之间的边所形成的轨迹。没有重复顶点的路径称为简单路径。路径的长度是路径上的边或弧的数目。
11、环:路径包含相同的顶点两次或两次以上。也就是说,在有向图的一条路径中,如果从某顶点出发,最后能够返回该顶点,则该路径是环。除了第一个顶点和最后一个顶点之外,其余顶点不重复出现的回路称为简单环或简单回路。
12、连通性:图中另一个重要的概念。对于无向图而言,如果它的每个顶点都能通过某条路径到达其他顶点,那么我们称它为联通的。如果该条件在有向图中同样成立,则称该图是强连通。尽管无向图可能不是连通的,但它扔然可能包含连通的部分,这部分分支为连通分支。如果有向图中只有部分是强连通的,则该部分称为强连通分支。
某些特定的顶点对于保护图或连通分支的连通性有特殊的重要意义。如果移除某个顶点将使得图或某分支失去连通性,则称该顶点为关结点。
三、图的存储方式
图的存储方式有:邻接矩阵、邻接表、十字链表、邻接多重表等等。这里先介绍一种存储方式:邻接矩阵。
1、邻接矩阵
邻接矩阵有向图是指通过邻接矩阵表示的有向图。
2、图的输入
先输入顶点数和边数:
4 8
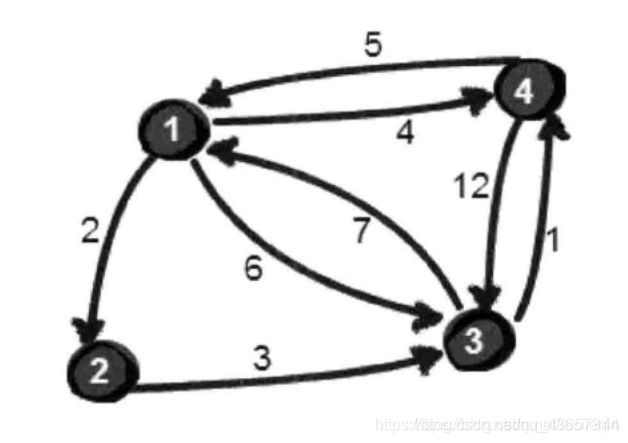
剩下8行输入8条边(三个数字分别表示:从a到b,权值为c):
1 2 2
1 3 6
1 4 4
2 3 3
3 1 7
3 4 1
4 1 5
4 3 12
如图所示:
该图(G)是由4个顶点(V)、以及8条边(E) 组成的有向图,如果我们用邻接矩阵表示该图,需要用一个二维数组e[MAXN][MAXN]来存储顶点与顶点之间的权值(若为无向图、权值为1、并且沿着对角线对称);
其中:

得到邻接矩阵为:

(INF为计算机所允许(不溢出)极大值、表示没有边。)
实现代码:
#define MAXN 60
#define INF 999999
int e[MAXN][MAXN];
int V,E;
void prepare()
{
for(int i=0;i> V >> E; //输入
for(int i=0;i> a >> b >> c;
e[a][b]=c; //从a到b的权值为c
}
}