2020年3月第三周学习心得
学习内容
本周对于贪心算法的学习暂时告一段落,但是平时的回顾和总结也不能落下,时常回头温故知新也是非常重要的:)
在这里浅谈一下对于贪心算法的总结:
贪心算法是从问题的初始状态出发,对于问题的每个阶段寻求最优解的策略。
贪心策略是在每次决策时都采取当下最优策略,做出的结果是某种约束条件下的最优解,并不一定是全局的最优解,此时应当对于具体问题具体分析,摸清题目要求以及解题思路。
- 建立数学模型来描述问题;
- 把求解的问题分成若干个子问题;
- 对每一子问题求解,得到子问题的局部最优解;
- 把子问题的局部最优解合成原来问题的一个解。
根据要求不断选择,以便于达到目的。
贪心并不仅局限于对问题的排序求解,有些问题也需要思路进行灵活转换。
下周就要开始动态规划的学习,对于动态规划也是早有耳闻,但是思路层次更加深层,应该比贪心还要困难,一定要研究深刻。
问题解决
特殊密码锁
有一种特殊的二进制密码锁,由n个相连的按钮组成(n<30),按钮有凹/凸两种状态,用手按按钮会改变其状态。
然而让人头疼的是,当你按一个按钮时,跟它相邻的两个按钮状态也会反转。当然,如果你按的是最左或者最右边的按钮,该按钮只会影响到跟它相邻的一个按钮。
当前密码锁状态已知,需要解决的问题是,你至少需要按多少次按钮,才能将密码锁转变为所期望的目标状态
输入
两行,给出两个由0、1组成的等长字符串,表示当前/目标密码锁状态,其中0代表凹,1代表凸。
011
000输出
至少需要进行的按按钮操作次数,如果无法实现转变,则输出impossible。
1刚开始我认为只需要从第一个按钮进行枚举判断就足够了,但是代码实现是错误的,所以我又重新检查了一遍,结果发现问题出在开头。
-
一个按钮如果按了第二下,就会抵消上一次按下所产生的影响。
因此,一个按钮只有按或者不按两种情况,不存在一个按钮要开关多次的情况。
例如八个 00000000
按1后 11000000
按3后 10110000
按1后 01110000
这和八个 00000000
只按一次3 01110000
是完全相同的情况 -
我们只需要考虑是否按下第一个按钮。因为如果第一个按钮的状态被确定了,那么是否按下第二个按钮也就决定了(如果第一个按钮与期望不同,则按下,如果期望相同,则不按下)同理,第三个按钮是否按下也唯一确定。所以,本题只要分两种情况:按钮1被按下和没有被按下之后使用for循环判断别的按钮是否需要按下即可当循环结束,若现在的按钮与答案相同,则输出两种方案中按键次数最少的,若不同,则impossible
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include 寻找平面上的极大点
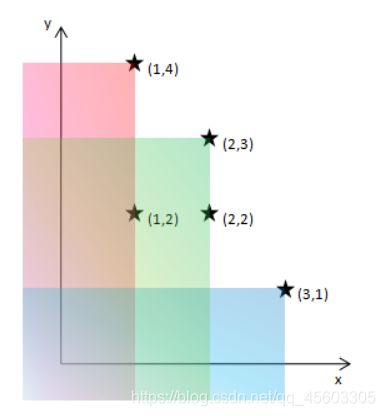
在一个平面上,如果有两个点(x,y),(a,b),如果说(x,y)支配了(a,b),这是指x>=a,y>=b;用图形来看就是(a,b)坐落在以(x,y)为右上角的一个无限的区域内。
给定n个点的集合,一定存在若干个点,它们不会被集合中的任何一点所支配,这些点叫做极大值点。
编程找出所有的极大点,按照x坐标由小到大,输出极大点的坐标。
本题规定:n不超过100,并且不考虑点的坐标为负数的情况。
输入
输入包括两行,第一行是正整数n,表示是点数,第二行包含n个点的坐标,坐标值都是整数,坐标范围从0到100,输入数据中不存在坐标相同的点。
输出
按x轴坐标最小到大的顺序输出所有极大点。
输出格式为:(x1,y1),(x2,y2),...(xk,yk)
这道题调试了一遍又一遍,做题的时候脑袋不是很清醒,所以在细节部分一次又一次出错,判断条件错误、初始位置搞错等等一些很奇怪的点都被我踩中,不过思路还是很清晰的;
对于任意一个点,如果它的y值不小于任何一个点使这个“任何一个点”x值大于给定点的x值,那么该点为极大点。
#include
#include
#include
#include
#include
#include
#include 这个解法好像挺暴力的,应该可以优化,之后再思考一下。
Pearl Pairing
At Bessie's recent birthday party, she received N (2 <= N <= 100,000; N%2 == 0) pearls, each painted one of C different colors (1 <= C <= N).
Upon observing that the number of pearls N is always even, her creative juices flowed and she decided to pair the pearls so that each pair of pearls has two different colors.
Knowing that such a set of pairings is always possible for the supplied testcases, help Bessie perform such a pairing. If there are multiple ways of creating a pairing, any solution suffices.
输入
* Line 1: Two space-separated integers: N and C
* Lines 2..C + 1: Line i+1 tells the count of pearls with color i: C_i
8 3
2
2
4输出
* Lines 1..N/2: Line i contains two integers a_i and b_i indicating that Bessie can pair two pearls with respective colors a_i and b_i.
1 3
1 3
2 3
3 2在Bessie最近的生日聚会上,她收到N(2<=N<=100,000; N%2==0)珍珠,每个都涂上C种不同颜色之一(1<=C<=N)。
观察到珍珠N的数量总是均匀的,她的创意来了,决定配对珍珠,使每双珍珠有两种不同的颜色。数据保证存在答案。请帮助Bessie执行这样的配对,如果有多种创建配对的方法,任意输出即可。
说明 有8颗珍珠和3种不同的颜色。两个珍珠颜色为1; 两个颜色为2; 四个颜色为3。
Bessie将每种颜色3的珍珠与一种颜色1和2配对。
将最多的优先配对
这个题我感觉十分巧妙,既然数据保证存在答案,便思考什么样子的数据才会保证存在答案。然后我们发现每种颜色的数量不可能超过N/2,否则答案将无解,记录下每个珍珠的颜色,然后分成两组(因为N是偶数)由于不可能有颜色数量超过N/2,所以我们枚举N/2次,每次取两组的第i位,就可以百分百保证不会有重复。
#include
#include
#include
#include
#include
#include
#include
#include
#include 想法感悟
贪心实际上是非常有意思的一类算法,面对千变万化的题目也有千变万化是思路,另外,好像每个人的思路都是不同的,在平时可以多参考一下别人的想法,说不定就对上电波了。
快开学吧,残念。