最大流

最大流概念

管道网络中每条边的最大通过能力（容量）是有限的，实际流量不超过容量。
最大流问题(maximum flow problem)，一种组合最优化问题，就是要讨论如何充分利用装置的能力，使得运输的流量最大，以取得最好的效果。求最大流的标号算法最早由福特和福克逊于1956年提出，20世纪50年代福特(Ford)、福克逊(Fulkerson)建立的“网络流理论”，是网络应用的重要组成成分。

发现简史

最大流问题是一类应用极为广泛的问题，例如在交通网络中有人流、车流、货物流，供水网络中有水流，金融系统中现金流，等等。求最大流的标号算法最早由福特和福克逊于1956年提出，20世纪50年代福特(Ford)、福克逊(Fulkerson)建立的“网络流理论”，是网络应用的重要组成成分。

数学模型

最大流问题，是网络流理论研究的一个基本问题，求网络中一个可行流f*，使其流量v(f)达到最大， 这种流f称为最大流，这个问题称为(网络)最大流问题。最大流问题是一个特殊的线性规划问题，就是在容量网络中，寻找流量最大的可行流。
最大流问题可以建立如下形式的线性规划数学模型：

式中v(f)称为这个可行流的流量、发点的净输出量或收点的净输出量。∞一般用标号法寻求有向最大流比用求线性规划问题的一般方法要方便得多。
最大的标号算法还用于解决多发点多收点网络的最大问题，设容量网络G有若干个发点x1,x2,…,xm；若干收点y1,y2,…,yn，可以添加两个新点vs,vt，用容量为∞的有向边分别连接两个新点vs与点x1,x2,…,xm，点y1,y2,…,yn与vt，得到新的网路G‘。G’是一个只有一个收点和发点的网络，求解最大流问题即可都得到G的解。

网络流概念

图和收发点
一个图是由点集V={vi}和V中元素的无序对的一个集合E={ek}所构成的二元组，记为G=(V,E)，V中的元素vi叫做顶点，E中的元素ek，叫做边。
仅有一个入次为0的点vs称为发点(源)，一个出次为0的点vt称为收点(汇)，其余点为中间点，这样的网络G称为容量网络，常记做G=(V,E,C)。
容量和流量
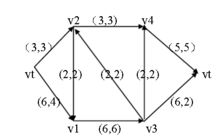
设有向连通图G=(V,E)，G的每条边(vi,vj)上的非负数cij称为边的容量。对任一G中的边(vi,vj)有流量fij，称集合f={fij}为网络G上的一个流。右图即为一个有向连通图，括号中第一个数字代表容量，第二个数字代表流量。

最大流问题

如图1-1，给你一个容量网络，假设要把一些物品从S送到T，问你T最多能收到多少物品。
图1-2，展示了一种可行方案，第一个数字表示流量，第二个表示容量。

这样的问题称为最大流问题(Maximum-Flow Problem)。
我们求解最大流问题有两种算法Edmonds-Karp和Dinic算法，利用增广路来求解。
1.Edmonds-Karp
我们先讲Edmonds-Karp算法，简称EK（我认为这种算法比Dinic慢）
如图1-3（红色表示当前选的路径），这个想法就是先找一条从S到T的可行路径，然后往这条路径上输入X个流量,X取决于这条路径上最小的流量（毋庸置疑，否则就将管道挤爆了）。

只要找到一条可行路径，就可以停下了。这时有人会问，如果这条路径的不是最理想的怎么办。这就用到反向的边了，如果有一条更优秀的，那么就会往回流，避免了这种情况，也就是网络流里很重要的一点。（想到这里，不禁开始膜拜那些大神了，这么优秀的方法都想的出来。Orz）
通过以上简单的讲述，这个算法基本讲完了，不过是多次BFS，然后将这条路径上所有的流量增加X。这就是Edmonds-Karp。
下面给出核心代码：
MAXN//点数
MAXE//边数
struct ad(){
int x,y,C,F;//表示从x到y的容量是C,流量是F。
}a[2MAXE];//因为有反向边，所以边数2
vector G[MAXN];//建立边表，存的是[x,y]这条边在a中的ID
int que[MAXN];//队列
int upd[MAXN];//用于更新当前最小的残量，如果upd[x]=0，表示这个点没被遍历过。
int fa[MAXN];//存储路径，从fa[y]走向y，方便增加流量
void Add(int x,int y,int c,int i){//i从1~MAXE
a[i]=xcw(x,y,c,0);G[x].push_back(i-1<<1);
a[i]=xcw(y,x,0,0);G[y].push_back((i-1<<1)+1);
}
bool BFS(){
hd=0;que[tl=1]=S;
memset(upd,0,sizeof(upd));upd[S]=1e9;
while(hd!=tl){
int x=que[++hd],L=G[x].size();
for(int j=0;j xcw E=a[G[x][j]];
if(!upd[E.y]&&E.C>E.F)
upd[E.y]=min(upd[x],E.C-E.F),que[++tl]=E.y,fa[E.y]=G[x][j];
}
if(upd[T]) return 1;//如果走到T就返回真值
}
return 0;//没走到返回假值
}
int Edmonds_Karp(){
int Flow=0;
while(BFS()){
for(int x=T;x^S;x=a[fa[x]].x)//枚举当前BFS走的路径
a[fa[x]].F+=upd[T],//加上当前最小残量
a[fa[x]^1].F-=upd[T];//相反边减去最小残量
Flow+=upd[T];
}
return Flow;//返回答案
}
一个问题供大家思考：为什么a[i^1]就是i这条边的相反边？
2. Dinic
这种算法其实和EK同一个原理，但是Dinic的更新过程却是不同的。
比如说是这样的一幅图：

如果用EK求解，那么就会成这样：

就会这么一直下去，如果在大一点，那么就会超时。
但是Dinic就能一步到位，只需一次DFS过程就可以实现多次增广（核心），他记录了当前节点的深度，用DFS去修正，但是在一定情况下又比EK慢，应为DFS修正也需要时间。
下面给出一段Dinic的代码：
#include
#include
#include
#define MAXN 10005
#define MAXE 200005
using namespace std;
int n,m,S,T,hd,tl,que[MAXN],dep[MAXN];
int tot=-1,lnk[MAXN],nxt[MAXE],son[MAXE],C[MAXE],F[MAXE];
int read(){
int ret=0;char ch=getchar();bool f=1;
for(;!isdigit(ch);ch=getchar()) f^=!(ch’-’);
for(; isdigit(ch);ch=getchar()) ret=(ret<<3)+(ret<<1)+ch-48;
return f?ret:-ret;
}
void add(int x,int y,int c,int f){son[++tot]=y;nxt[tot]=lnk[x];lnk[x]=tot;C[tot]=c;F[tot]=f;}
bool BFS(){
hd=0;que[tl=1]=S;
memset(dep,0,sizeof(dep));dep[S]=1;//更新点深度，可以说是刷层次
while(hd!=tl){
int x=que[++hd];
for(int j=lnk[x];j!=-1;j=nxt[j])
if(!dep[son[j]]&&C[j]>F[j]) dep[son[j]]=dep[x]+1,que[++tl]=son[j];
}
return dep[T];
}
int DFS(int x,int flow){
if(xT) return flow;//到T点就停
int now=0;
for(int j=lnk[x];j!=-1;j=nxt[j])
if(dep[x]+1dep[son[j]]&&C[j]>F[j]){
int y=DFS(son[j],min(flow,C[j]-F[j]));//选出最小流量
if(y>0){F[j]+=y;F[j^1]-=y;now+=y;flow-=y;if(!flow) return now;}//进行更新
}
return now;
}
int Dinic(){
int ans=0;
while(BFS())
while(int t=DFS(S,1e9)) ans+=t;
return ans;
}
int main(){
memset(lnk,-1,sizeof(lnk));
n=read(),m=read();S=read(),T=read();
for(int i=1;i<=m;i++){
int x=read(),y=read(),z=read();
add(x,y,z,0);add(y,x,z,z);
}
printf("%d\n",Dinic());
return 0;
}
四、最大流最小割
最大流最小割定理:网络的最大流等于最小割
是不是很懵逼。
我在网上看到一个人写的很好，给大家观摩一下。
具体的证明分三部分
1.任意一个流都小于等于任意一个割
这个很好理解 自来水公司随便给你家通点水，构成一个流
恐怖分子随便砍几刀 砍出一个割
由于容量限制，每一根的被砍的水管子流出的水流量都小于管子的容量
每一根被砍的水管的水本来都要到你家的，现在流到外面 加起来得到的流量还是等于原来的流
管子的容量加起来就是割，所以流小于等于割
由于上面的流和割都是任意构造的，所以任意一个流小于任意一个割
2.构造出一个流等于一个割
当达到最大流时，根据增广路定理
残留网络中s到t已经没有通路了，否则还能继续增广
我们把s能到的的点集设为S,不能到的点集为T
构造出一个割集C[S,T],S到T的边必然满流 否则就能继续增广
这些满流边的流量和就是当前的流即最大流
把这些满流边作为割，就构造出了一个和最大流相等的割
3.最大流等于最小割
设相等的流和割分别为Fm和Cm
则因为任意一个流小于等于任意一个割
任意F≤Fm=Cm≤任意C
定理说明完成，证明如下：

对于一个网络流图G=(V,E)

G=(V,E)，其中有源点s和汇点t，那么下面三个条件是等价的：

流f是图G的最大流
残留网络Gf不存在增广路
对于G的某一个割(S,T)，此时f=C(S,T)

f=C(S,T)

首先证明1 => 2：

我们利用反证法，假设流f是图G的最大流，但是残留网络中还存在有增广路p，其流量为fp。则我们有流f′=f+fp>f

f′=f+fp>f。这与f是最大流产生矛盾。

接着证明2 => 3：

假设残留网络Gf不存在增广路，所以在残留网络Gf中不存在路径从s到达t。我们定义S集合为：当前残留网络中s能够到达的点。同时定义T=V-S。
此时(S,T)构成一个割(S,T)。且对于任意的u∈S,v∈T

u∈S,v∈T，有f(u,v)=c(u,v)f(u,v)=c(u,v)。若f(u,v)0Gf(u,v)>0，s可以到达v，与v属于T矛盾。
因此有f(S,T)=Σf(u,v)=Σc(u,v)=C(S,T)

f(S,T)=Σf(u,v)=Σc(u,v)=C(S,T)。

最后证明3 => 1：

由于f的上界为最小割，当f到达割的容量时，显然就已经到达最大值，因此f为最大流。

这样就说明了为什么找不到增广路时，所求得的一定是最大流。
本来以为最小割很难，是我的书惹的祸，原来是这样子的啊！如果看不懂，那么你只要记住这个定理就可以了。
原文链接：https://blog.csdn.net/qq_41357771/article/details/79416899