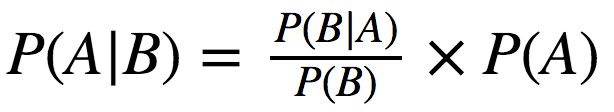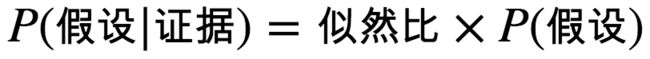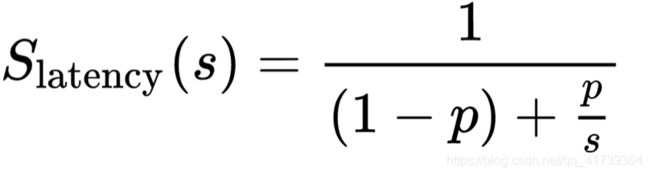喾哲~ (八月最佳)
《目录》
- 数学的起源
- 大数定律:
- 贝叶斯概率:
- 傅立叶变换:
- 哈夫曼编码:
- 最大熵原理:
- 幸存者偏差:
- 丑小鸭定理:
- 阿姆达尔法则:
- 马尔可夫模型:
- 学者存在性定理:
- 奥卡姆剃刀法则:
- 柯尔莫哥洛夫复杂度:
- 哥德尔不完备定理:
- 二进制编码的有效性:
- 中心极限定理与三大分布模型
- 数学期望、标准差、正态分布
- 费马大定理、可证伪性、回归平均
- 启发式、没有免费午餐定理、最小最大值定理
读书不能如追星,仰望、仰望着世界,得试着俯视,才有钻研学问的感觉。
数学公式看不懂 ,直接看数学原理背后的哲学结论好了,因为哲学就是时时刻刻试图触及事物的本质,我们来一起探索......
数学的起源
对一般人来说,数学意味着数字和计算,但其实数学远比这个答案要复杂得多,数学是研究数量、结构、变化、空间以及信息等概念的一门学科。
一般,数学可以分成三个部分,几何、分析和代数。
- 几何(geometry),是描述静态物体空间关系的。
- 分析(analysis), 是用来处理物体随时间改变和移动的,像微积分就属于分析。
- 代数(algebra), 是帮助我们用数字、符号和方程式来处理信息的。像群论、图论和拓扑学都属于代数的范畴。
对于人类来说,数学是为人类自身的生存而发展出来的能力。
为了让数学具备 简洁、直接、齐整的特性,人们把数学发展为了一门 符号语言。
在原始社会时,人需要知道 什么时候夜幕会降临,遇到危险怎么找到最快的路径离开,最有可能找到食物的地方......
现在呢,要抓住一个飞来的球,在拥挤的地铁上穿行,开车...... ,这些数学计算对于人是不自知,虽然数学计算是默认的,但并不意味着头脑里的计算一定、一直是对的。
举个 “赌徒谬误” 的例子。
我在玩俄罗斯轮盘赌,小球第一次停在了红色区域,我会觉得,下一次小球出现在黑色区域的可能性会更大,但是从数学概率上来说,其实每一次的概率都是 50%。
那为什么我会觉得,小球再一次出现在红色区域的概率不如出现在黑色区域的大呢 ?
这是因为在我们祖先的生活经验里,在一个地方生活过一段时间,把那里的食物采集得差不多之后,就必须换地方了,不然没东西可以吃了,所以从生存经验上来说,出现过一次的事件,不太可能出现第二次,这种认知模式被保留下来,就出现了“赌徒谬误”。
像大脑的自动计算,目前机器还不能完全做到,如无人驾驶就不能适应 各种各样又随时变化 的路况。
数学,能告诉我们所有生物的寿命极限、绝对力量(一次举重最大重量)、形态(为什么长到一定程度就不能长高了)、毛细血管为啥是四维的......
- 接电话,听到一个甜腻腻的声音,啊,肯定对面是一个美女 !!!
- 女生觉得某个男孩帅,那 TA 一定也聪明,说不定性格也好......
从数学上分析,几个小概率事件组合再一起的概率只会更小。
您 遇见/即将遇见 的那位,更多的是,是拥有 大概率 事件的人,除非您特别特别的特别。
见过某位黑客找女朋友,啧啧,没谁了。
大佬认为像我这么优秀的人,必须找一位才貌双全的女子。
美貌第一,那女朋友的长相应该在人群的俩个标准差之外(比 97.5% 的女性美,剩下的 2.5%)。
智商也得比较高才行(为后代着想),大佬认为简单点,就一个标准差吧(从 2.5% 中再选 16%)。
现在就剩下 0.4%,而她还必须和大佬年龄相仿、单身、和大佬相互吸引......
这么算下来,全球大约只有 几千女性 是大佬的结婚对象。
嗯,大佬得到了一个结论 :就现在的相亲模式,“我” 用数学方法证明了自己一辈子(几乎)找不到女朋友。
数学的作用是帮助我们克服经验和感觉带来的不精确,让我们不但可以超越自身的感觉来理解世界和宇宙,还可以使用数学语言来对抽象的概念进行深入的探索。
大数定律
重来一次,人生也并不能改变什么。
1939年,南非数学家克里奇冒失地跑到欧洲,结果被关进集中营。
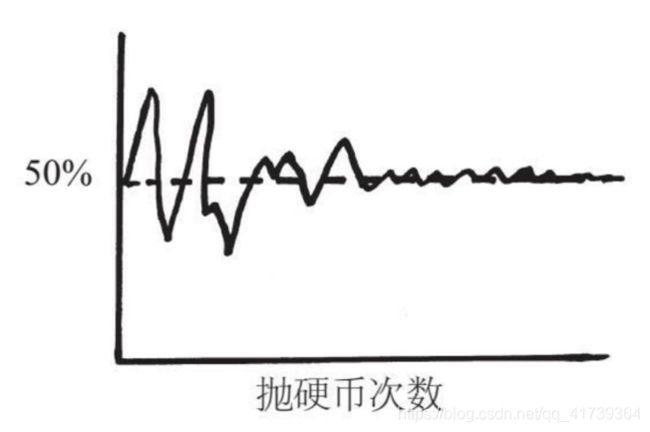
百无聊赖的时候,他给自己找到了一个有趣的乐子:一枚硬币抛了1万次,记录了正面朝上的数量。
统计结果:
图中的折线,一开始结果偏离 50% 特别远,很多次都是正面。
随着抛硬币的次数越来越多,正面朝上的概率明显地向 50% 靠近。
其实,计算机模拟的结果也是这样:
- 抛 10 枚硬币,正面朝上的比例范围是 30%~90%;
- 抛 100 枚,比例范围就缩小了,变为了 40%~60%;
- 抛 1000 枚,比例范围就缩小到 46.2%~53.7%。
越来越接近 50%,那是不是有一种神秘力量,让结果不断逼近50%呢?
其实这靠的是,大数对小数的稀释作用。
大数定律不会对已经发生的情况进行平衡,而是利用新的数据去削弱Ta的影响力,直到前面的数据从结果上看,影响力非常小,可以忽略不计。
如果我们人生中犯了一两个错误,也不要纠结,我们应该用更多正确的事,把这件事稀释掉。
生活中,我们很难像监狱里的数学家一样,扔 1 万次硬币来验证一件事。
但当您真正理解了大数定律,在这类问题面前,您就能作出更正确的决策。
假如您现在可以搭乘一部时光穿梭机,改变您人生中任意一件事,您能否改变自己的命运?
我们往往把人生的问题,归结为嫁错人,选错专业,进错公司。
改变这些选择,能改变我们的人生吗?
我们都知道那句人生格言,人生关键的就那么几步,选错了就选错了。
那我去改变关键选择不就好了吗,但为什么说这样不起作用呢?
理解了大数定律,您就能理解为什么穿越不能改变命运。
就像买股票,预言家告诉您:“现在是茅台的最低价位一个机会,一定要全仓买入茅台。”
能您觉得你会发财吗?
不会啊。因为您可能在下一次危机中,加杠杆就赔得倾家荡产。
这样的故事我们见得还少吗?
获得彩票大奖的人,后来就会一生幸福吗?
并不是。根据统计,许多美国彩票中奖者后来过得都不怎么样,因为一次的飞来横财,并不会让一个人的生活更美好。
赌博怎么都是输的:
- 输了,继续赌还是输;
- 赢了,继续赌,随着赌注的增加,只会输的更多,倾家荡产是完全可能的;
一个硬币即使连续 20 次出现正面,但是如果连续抛很多次的话,正面出现的概率还是 50%。
也就是说,硬币的命运,是由Ta自身的结构所决定的。
当样本量足够大的时候,大数定律就开始发挥作用。
当我们讨论一生的命运时,我们的个人命运不取决于一两次选择,而取决于我们的系统。
所以,“性格决定命运”这句话,应该修正为:性格决定行为方式,行为方式决定命运。
您的行为方式就是那个决定您命运的系统。
就算有时光穿梭的机器,回到过去甩了男友、换掉老板,最后的命运可能还是一样。
面对人生的大数定律,我们该怎么办呢,因为我对现在的自己还不太满意,但我又想改变!
我们可以先业界的前辈学习经验,比如,澳门赌场。
以澳门赌场的美式轮盘为例,赌场的概率优势只有 2.7%,看起来很小,但是凭借“大数定律”的魔力,能够稳稳地形成对赌客的概率压制。
所以,改变系统也不用您做对人生中的每一件事,做好每个选择,只需要您把人生系统的指针,向正确的方向拨一点。
但别小看这一点点偏差,就是这点偏差,会引领我们走向完全不一样的人生轨道。
遇事顺不顺其实在心,所有看问题的角度都可以概括为对【挨一耳光】的反应:
- 扇回去:太强势与生活里的人、事都要斗一斗,结果谁都斗不过,失去了一切;
- 认怂,捂脸离开:一辈子都懦弱、胆小怕事,失去了自我;
- 先冷静分析一下:卒然临之而不惊,无故加之而不怒,人是可以成长、改变的,必然有出路。
学习、做事、工作都会不断的遇到【挨一耳光】的事,不知道,我一直走的哪种呢?
从短期来看,人生充满偶然,充斥着不尽的选择;而长期呢,每个人的生命是必然的。
调整我们自己的人生系统,坚持做正确的事情,也许会比暴富一次更能让人满足和幸福。
除此之外,大数定律还可以打三国杀。
因为在 8v8、国站经常会有冲动的孩子,盲打。
我被盲打后,就想跳了。
不过,有大数定律之后,我明白要想让我总的个人战绩很好看,我必须原谅那冲动的孩子,忽略我还做不到。
如果您追求总战绩的美观,在这里,送上打三国杀的秘笈:
- 菜鸡报复
- 老手原谅
- 高手忽略
说到命,很多中国人脑海里难免会受到算命的影响,从而潜意识里去认命,可其实如果具体去看什么决定了每一个人的命,是选择,而合理的选择是建立在方法论上,好的方法论,离不开有一个正确的价值观,说到底,多数时候我们认命是默认了自己粗糙的价值观。
能认识自己的人,知道如何去改变自己,也知道哪些是自己能够左右的,哪些是自己无法改变的。当一个人意识到自己的一生除去运的那部分是可以改变的,潜意识也会跟着改变。
贝叶斯概率
如何漂白王境泽的真相定律 ?
还记得,小时候书本上的文章 《狼来了》?
今天学了贝叶斯概率后,可以试着推一下小孩子每次说 狼来了 的可信度分别是多少,最后您就知道为什么村民不相信 ta 了。
- 超乎寻常的论断需要超乎寻常的证据。
那么如何量化证据和论断的联系呢 ?
贝叶斯说,您对某个假设的相信程度,应该用一个概率来表示 —— P( 假设 ) 。
用 概率 定义了 信 和 不信,P = 1 就是绝对相信,P = 0 就是绝对不信,P = 15% 就是有一点信。
先把 信仰 给量化,有了新的 证据 我们就更新这个概率,变成 —— P( 假设|证据 ) ,这个叫条件概率。
名词解析:
信仰:对某种思想、宗教、某人、某物的相信程度。
证据:可以证明事件事实的材料。
概率:用
表示某事情发生的 可能性大小(有可能发生,有可能不发生) 的一个量。
一般来说,P( A|B ) 的意思是 “在 事件B 是真的条件下,事件A 的概率”。
咱们举个例子,A 表示下雨,B 表示带伞。一般来说这个地方不常下雨,所以 P(A) = 0.1。
但今天您注意到爱看天气预报的老张上班带了伞,那就可以推断,今天下雨的概率应该增加 —— 在 “老张带伞” 这个条件下的下雨概率,就是 P( A|B )。
俩个因果关系:
- 缘故 → 结果,在这里就是 “下雨 → 带伞” 即 A → B。
- 结果 → 缘故,在这里就是 “带伞 → 下雨” 即 B → A。
A → B 和 “老王是凶手 → 在老王家里找到凶器”,ta 们都相当于 “假设 → 证据”。
现在我们想算的是 P(假设|证据),是从结果倒推缘故,这叫“逆概率”,这个不好算。
一般都是从缘故推结果容易算,如您看见一个小孩向窗户扔球,您可以估计窗户被打碎的概率有多大,这是“正向概率”;但如果您看到窗户碎了,想要推测窗户是怎么碎的,那就无法确定了。
所以咱们要算的是一个逆概率,这要怎么算呢 ,有一个贝叶斯的方法。
为了计算 P( A|B ),我们考虑这么一个问题:A 和 B 都发生的概率有多大 ?
这道题有两个算法。
一个办法是先算出 B 发生的概率有多大,是 P(B);再算 B 发生的情况下,A 也发生的概率有多大,是 P( A|B ),那么 A、B 都发生的概率,就是把这两个数相乘,结果是 P( A|B )×P( B )。
同理,先考虑 A 发生再考虑 A 发生的条件下 B 也发生,结果是 P(B|A)×P(A)。
这俩的结果一定相等,P( A|B )×P( B ) = P( B|A )×P( A ),求 逆概率P( A|B ) 即:
举个贝叶斯概率应用的例子,如果您真的读懂了,那类似的问题都可以自己解决,如狼来了。
有一位 40 岁的女性去做乳腺癌的检查,检查结果是阳性。那请问,这位女性真的得了乳腺癌的概率有多大。
我们用 A 表示她得了乳腺癌,B 表示测试结果为阳性,这个因果关系是乳腺癌导致阳性, A → B。我们要计算 P(A|B)。根据贝叶斯公式,我们需要 P(A),P(B) 和 P(B|A)。
在有新证据之前,P(A) 就是一般相同年龄段女性得乳腺癌的概率,统计表明是 ![]() 。
。
P(B|A) 是如果这个人真有乳腺癌,她的监测结果为阳性的可能性。这是由检测仪器的敏感度决定的,答案是73%,仪器并不怎么准确。
P(B) 是随便找个人,给她检测出阳性的可能性是多大。这个我们没有直接的数据,要拆成这个人有乳腺癌(A)和没有乳腺癌(~A)两种情况,其中 P(~A) = 1-P(A) = ![]() 。
。
刚才说了有乳腺癌、检测为阳性的概率是73%。而没有乳腺癌的人还可能会被误诊成阳性,已知这个误诊率是 P(B|~A) = 12%。
于是, P(B) = P(B|A)×P(A) + P(B|~A)×P(~A) = 12.1%。
把这些数字带入公式,我们最终得到 P(A|B) = ![]() 。
。
也就是说,哪怕这位女性被检测出来是乳腺癌阳性,她真得乳腺癌概率也只有不到 1%。
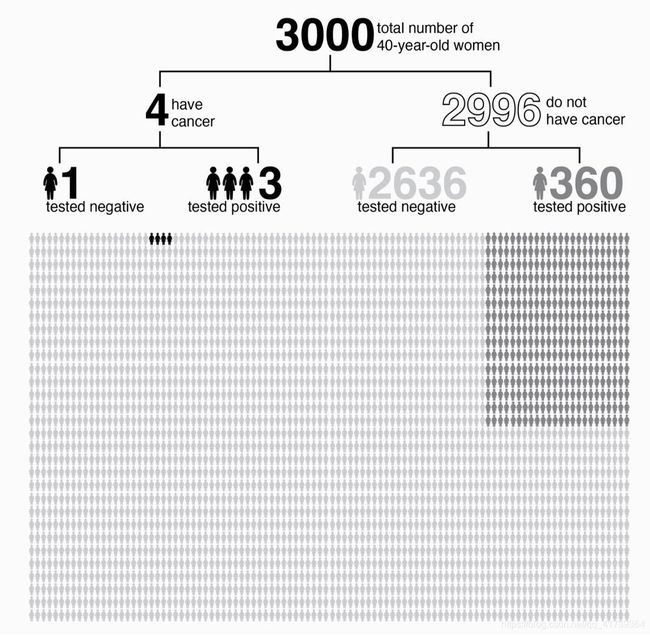
这是一个非常出乎意料的结论。但是贝叶斯公式不是什么黑箱操作的魔法,您还可以用下面这张图参详一下。
假设有 3000 名 40 岁的女性,根据前面说的各项数据,其中只有 4 人真有乳腺癌,而被正确检测为阳性的只有三人。另一方面,被检测仪器误诊为阳性的,却有 360 人。所以在所有阳性诊断之中,只有不到 1% 的人真有乳腺癌。
出现这种情况的根本原因就在于乳腺癌的患者比例很小,而检测仪器又很不准确。
几乎每一本讲贝叶斯方法的书都会使用一个这样的例子,您想明白一个就想明白了所有的。
请注意,如果这位女性本身携带容易得乳腺癌的基因,那我们一开始选用的 P(A) 就不是 1/700 了,而应该是 1/20。用这个数算,最后的 P(A|B) = 1/3,这就非常不一样了。
这是一个关键问题。一开始,您到底凭什么选择 P(A) 的数值呢?
那是您自己的主观判断。
这就是为什么有很多统计学家攻击贝叶斯方法,人们总是觉得科学方法应该是完全客观的才对!
但贝叶斯方法实际上是对科学方法的重大升级。
传统的科学方法,是
- 1. 提出一个理论假设;
- 2. 做实验验证;
- 3. 如果实验结果符合理论,这个理论就暂时站得住脚,如果不符合,理论就被证伪了。
这是非黑即白的剧情,理论要么就继续保留,要么就彻底抛弃。
而贝叶斯方法则是先给理论假设设定一个可信度。
新证据并不直接证实或者证伪理论,只是调整可信度的大小,做一个动态的判断。
贝叶斯方法是一种实用主义的态度,其实咱们想想,我们搞研究的目的并不一定是了解 绝对真实 的世界 —— 我们现在的数学定理也只是再发现世界和宇宙的规律,如同人在丛林的冒险—— 我们的目的是通过获取实用的知识,做出尽可能准确的判断和决策。
贝叶斯公式可以写成:
您可以把 ta 理解成 “观念更新” 的公式,P(假设) 是老观念,新证据发生之后,您的新观念是 P(假设|证据)。
新观念 = 老观念 * 似然比。
您的观点,随着事实,发生了改变。
贝叶斯定理让我想到了一群牛人,那就是企业家:
- 1、马云当年说无论如何都不会做游戏,而现在游戏已经是阿里很重要的一块业务。
- 2、小米最开始出手机时,说手掌大小的手机最适合,绝对不会做大屏手机,而现在手机越做越大。
- 3、罗永浩说手机绝对不会低于3000块,后来果断降价了。
- 4、罗振宇说罗辑思维视频节目要做10年。做了不到一半就停更了。
我之所以说出以上这些案例,不是为了嘲笑他们的不坚守(那是傻子做的事),我想一定是他们的认知升级了,他们随着环境条件的变化刷新了自己的认知,立即产生了行动。 我想这是他们今天如此成功的原因。 不是傻傻的坚守一个看似坚定不移的信念或者对自我的承诺,而是认真的观察这个世界发生的一切而随时矫正自己的行为方式。 这就是牛人。 所以如果说谁对贝叶斯定理运用的最好,一定是成功的企业家,因为他们是真金白银的在这个竞争残酷的世界做每一次选择。
我们设想一下,如果每个人的阅历和想法不同,一开始的观点不一样,那么哪怕是面对同样的证据,人们更新之后的观点,也还是不一样的!
所以贝叶斯方法本质上是个主观的判断方法:同样的证据,贝叶斯方法允许您有不同的判断!!!
我们首先有一个初始信念,被称为先验,当我们获得额外的信息后可以对这个信念进行修正更新。
- 1. 先评估一下自己的信念,设定 P(信念);
- 2. 等待新证据;
- 3. 证据出来以后,用贝叶斯公式更新自己的信念,计算 P(信念|证据);
- 4. 继续等待新证据……
还有更秀的:
- 看过神雕侠侣,年龄不是问题;
- 看过金刚,种族不是问题;
- 看过倩女幽魂,生死不是问题;
- 看过断背山,性别也不是问题。
从哲学角度来说,贝叶斯概率是 理解差异。
上次聊天时,朋友说我们三观不一样、聊不下去。
如果用贝叶斯想一下。。。。。。
其实这很正常,说明开始的时候你们互相并不了解嘛。
西方有一句谚语说:我们因为不了解而走到一起,因为了解而分手。
年轻人交友容易这样,开始时把友谊想得很完美,然后就用这个完美的标准去要求友谊,结果一定出问题。
在友谊中,不能没有宽容,要尊重双方的差异。
回想交朋友时,开始时是不是太轻率,后来是不是太苛求。
不过,这很难,因为人很难保持开放哦~
所谓开放是让人可以放下成见、情绪、旧东西,合理的面对不同的观念,并且不陷入认知偏误,这很难的。
傅立叶变换
您写的文章真的是 原创 吗?
十九世纪法国数学家 傅里(立)叶 发现任何周期性的函数(信号)都等同一些三角函数的线性组合。
从哲学角度来说,傅里叶变换是把一个复杂的事物拆解为一堆标准化的简单事物的方法。
如,跳舞这个复杂的动作由腿部、手部、肩部、腰部等单一的动作组成。
举一个相关的例子,傅里叶运用于声音中。
声音是空气的震动,手指轻轻地弹一下碗,我们会听到 悦耳的声音。
声音由 音调 和 音量(响度) 组成,音调是震动的频率,音量是震动的幅度。
![]()
上图的正弦曲线,也是一个简单的声音。
这个声音呈完美周期性的变换、频率是固定的。
而一个复杂的声音,就是由这样简单的声音组成。
![]()
因此,傅里叶变换在声音的领域中即:
由一系列简单的波动如搭积木一般组成一个复杂的波动,看下图。
![]()
图中俩条红色的曲线,都是由那些蓝色的波形叠加而出。
傅里叶变换最核心的是可以告诉我们,图中红色曲线是由多少组成比例的蓝色曲线构成。
红色曲线 = 频率是 100 的蓝色曲线 × 0.5 + 频率是 200 的蓝色曲线 × 0.2 + 频率是 300 的蓝色曲线 × 0.1 + 频率是 400 的蓝色曲线 × 0.08 + ……
取出蓝色曲线的数值成分:红色曲线 = (0.5, 0.2, 0.1, 0.08, ......)。
写一篇文章,会参考许多资料;那这篇文章,就可以拆分为 《XX》*0.1 + 《XX》*0.2 + ......
所以,现在大部分原创经常是已知的、简单的事物的排列组合。
这里说的是,傅里叶变换的思想原理,而其中更加有趣的地方,您可以看看:
- 《傅里叶变换的终极解释》(上)
- 《傅里叶变换的终极解释》(下)
- 《用傅里叶变换画出任何简笔画》
从哲学角度来说,傅里叶变换是把一个复杂的事物拆解为一堆标准化的简单事物的方法,大道至简。
哈夫曼编码
如何创造一门数字语言 ?
前置知识:二进制编码的有效性。
我们在谍战片中经常看到报务员还没有发完报,敌方的特工就冲了进来,这种场景并不完全是虚构的,因为在二战时欧洲德占区这种情景时常出现,因此省一点时间就意味着自身的安全。
即使不考虑战争中的特殊情况,省掉三分之一的通信成本,也是很可观的。
现在我们来设计一个用于英文通信的编码系统吧,特点:最短、易用。
英文通信系统由 26 个字母组成,为了拥有 易用 这个特点,我们选择最基础的二进制作为整个编码系统的最小单元(而且二进制和机器配合的最好)。
26 个英文字母都由 0 和 1 来代替,那么任何设计呢 ?
首先思考几个问题:
- 需要多少二进制位才能表示 26 个字母 ?
- 二进制位怎么对应一个字母才是最优的 ?
- 到底是等长编码的平均编码长度少,还是不等长编码的平均长度少 ?
搞清楚上面的 3 个问题,您就可以自己造出著名的摩尔斯电码,甚至还可以优化 !!
[名词解析]
等长编码:表示 26 个英文字母的二进制长度是一样的。
不等长编码:表示 26 个英文字母的二进制长度不一样。
平均编码:表示 26 个英文字母的二进制总长度 / 26 得出的平均长度。
举个例子,等长编码下 B 是 10,那 A 是 1,有等长这个条件 A 就需要补一个零,A 即 01,B 即 10。
不等长编码下 B 是 10,那 A 是 1,莫尔斯电码就是不等长编码。
- 需要多少二进制位才能表示 26 个字母 ?
显然是 5 个,表示 26 个字母的任意一个就是 26 选 1 啦。
信息量是 ![]() ,结果是约(向上取整)是 5 比特。
,结果是约(向上取整)是 5 比特。
- 二进制位怎么对应一个字母才是最优的 ?
个人觉得经常出现的字母要采用 容易敲的(等长编码)/较短(不等长编码) 的编码,不常见的字母就采用较长的编码。
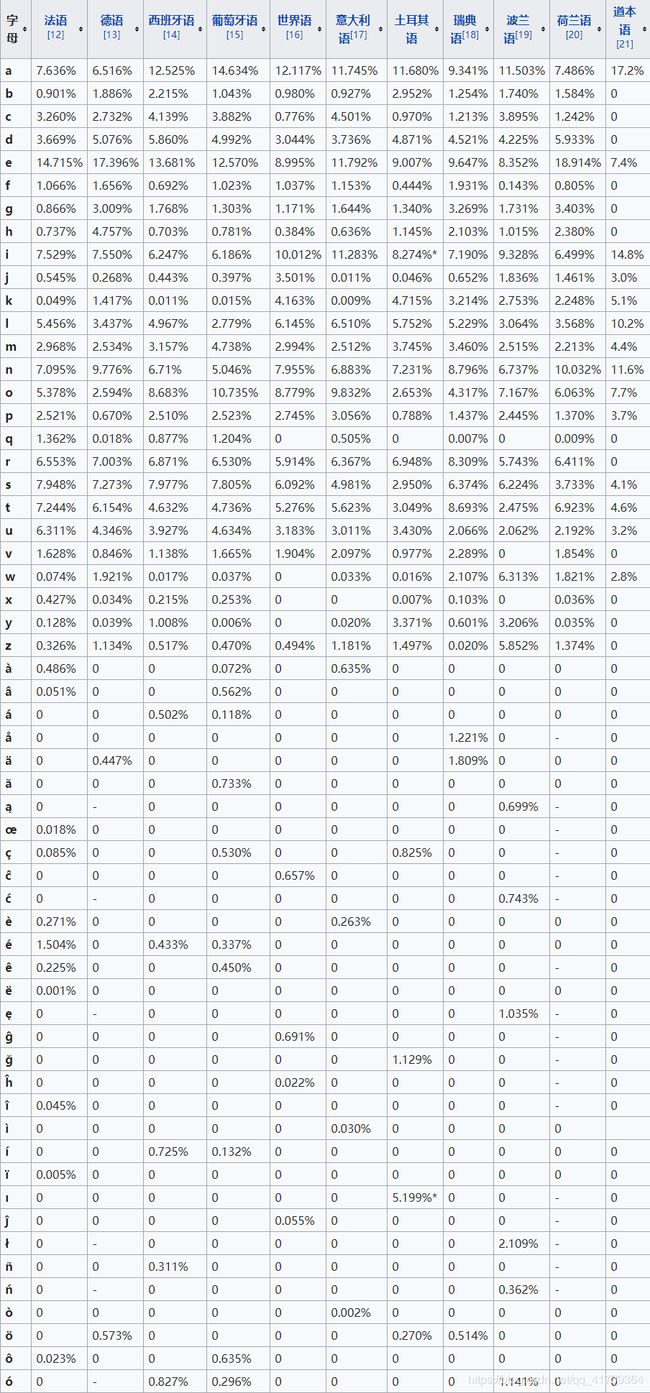
下图是一些自然语言的频率统计,更加具体的请见博客:《密码学》。
著名的莫尔斯电码没有严格的按照字符的频率来设计,因此,哈哈,莫尔斯电码还可以改进一下哈。
- 到底是等长编码的平均编码长度少,还是不等长编码的平均长度少 ?
著名的莫尔斯电码(不等长编码)采用的也是二进制,平均编码长度是 3;而使用等长编码系统的平均长度是 5,显然不等长编码长度比等长编码长度要划算......
证明:
假定有 32 条信息,每条信息出现的概率分别为 ![]() 、
、![]() 、
、![]() 、
、![]() ……
……
依次递减,最后 31、32 两个信息出现的概率是 ![]() 、
、![]() ( 此时 32 个信息的出现概率之和就是 1 )。
( 此时 32 个信息的出现概率之和就是 1 )。
用二进制数对 ta 们进行编码。
等长度和不等长度两种编码方法,我们来对比一下:
- 方法一:采用等长度编码,码长为 5。因为是 log32=5 比特。
- 方法二:不等长度编码,如果出现概率高就短一些,概率低就长一些。
我们把第一条信息用 0 编码,第二条用 10 编码,第三条用 110 编码……最后 31、32 两条出现概率相同,都很低,码长都是 31。
第 31 条信息就用 1111……110( 30 个 1 加 1 个0 ) 编码,第 32 条信息,就用1111……111( 31个1 ) 来编码。
这样的编码虽然大部分码的长度都超过了 5,但是乘以出现概率后,平均码长只有 2,也就是说节省了 60% 的码长。
如果利用这个原理进行数据压缩,可以在不损失任何信息的情况下压缩掉 60%。
这种方法最早是由 MIT 的教授 哈夫曼 发明的,因此也被称为 “哈夫曼编码”。
哈夫曼编码从本质上讲,是将最宝贵的资源(最短的编码)给出现概率最大的信息。
资源分配原则:一条信息编码的长度和出现概率的对数成正比。
如在上面的例子中,第一条消息出现的概率为 ![]() ,我们知道
,我们知道 ![]() (以二为底) 的对数等于 -1,因此TA的编码长度就是 1 (即码 0);最后俩条消息出现的概率为
(以二为底) 的对数等于 -1,因此TA的编码长度就是 1 (即码 0);最后俩条消息出现的概率为 ![]() 次方,取对数后等于 -31,因此TA们的编码长度就是 31。
次方,取对数后等于 -31,因此TA们的编码长度就是 31。
从哲学角度来说: 闲暇出智慧,所谓闲暇是有时间花在自己身上(热爱的领域)。
金钱 < 时间 < 注意力(对别人凡是不妨碍我达成目标的事,我都可以替 TA 服务),
最大熵原理
我知道我会在哪里死,又如何 ?
每郑一次骰子 ?,1 - 6 的可能性都是 ![]() 。
。
每个面的可能性都是相同的,这是在理想环境下。
那么,不理想的环境是什么呢 ??
骰子 ? 质地分布不均匀、且各个面的形状有差异。
骰子毕竟是实体,因此,每个面的概率大多数情况下不是平均分布的,会多也会少呀。
当我们使用的骰子就是上面这颗不均的骰子,那我们该如何去赌呢 ??
其实还是应该猜 ![]() ,概率均摊让风险最小。
,概率均摊让风险最小。
现在经统计得到了此骰子 ? 郑到 3 点的概率是 ![]() ,而 3 点对面的 4点(对应面之和是7) 的概率几乎为 0。
,而 3 点对面的 4点(对应面之和是7) 的概率几乎为 0。
现在,我们又该如何去赌呢 ??
总概率 1 减去 3 、4 点的概率和,再把结果概率均摊到其余的 1、2、5、6 点,均摊的 4 点概率是 ![]() 。
。
采用均摊是因为在不知道别的信息的条件下,均摊的风险最小,均摊为什么让风险最小呢 ?
因为我们没有对未知的情况作出如何主观的假设,我们的预测都在当前已知的信息下决定的;均摊就如一句话:“不要把所有的鸡蛋 ? 放一个篮子里”。
第一次,我们得到的信息是:骰子质地不均。
虽然我们知道概率发生了变化,但并不好主观的假设。
第二次,我们得到的信息是:骰子质地不均、3 和 4 点出现的概率之和是 ![]() 。
。
我们知道了 3 点、4 点的概率是 ![]() 和 0,其余各点均摊为
和 0,其余各点均摊为 ![]() 。
。
最大熵原理即:当我们需要对一个随机事件的概率分布进行预测时,我们的预测应当满足全部已知的条件,而对未知的情况不要作任何主观假设。
最大熵原理简直就是在复述我们郑骰子的过程,不是嘛 !!
我们按照上述的流程,建立一个概率的模型,这样的模型会使得 不确定性 达到最大,因此,得名为 “最大熵模型”。
名词解析
熵:不确定性。
记住啦,使用当前的信息就好,不要自作主张得想进一步减低不确定性而作出需要主观的假设,这样预测反而越不准确。
从哲学角度来说:最大熵原理如 过犹不及。
幸存者偏差
妈妈为什么不挑食 ?
讲一个小故事,也是 2018 年的高考作文题。
在第二次世界大战期间,美国军方在哥伦比亚大学建立了一个秘密研究小组,叫统计研究小组。
TA 的任务是组织美国的统计学家为打赢第二次世界大战服务。这个小组里牛人无数,如我们熟悉的控制论的创始人诺伯特·维纳(Norbert Wiener),还有后来得过诺贝尔经济学奖的米尔顿·弗里德曼。
不过,在这个牛人无数的小组中,天赋最高的并不是他们,而是一位叫亚伯拉罕·瓦尔德(Abraham Wald)的数学家。
美国军方认为,如果每次战斗中,自己被击落的飞机比对方少 5%,消耗的油料低 5%,弹药多 5%,机动性高 5%,就会最终成为胜利方。这个结论也是有数学依据的,不是假设。
因此,军方给这群数学家出了一道题。在打仗的时候,为了不让自己的飞机被敌人的战斗机击落,需要给飞机装上装甲。但是,装甲会增加飞机的重量,这样飞机的机动性就会减弱,还要消耗更多的燃油。
因此,需要解决的问题是,怎样在防御性能和飞行性能之间找一个平衡点。军方希望数学家帮助他们搞清楚,在哪里加强装甲防护是最合适的。
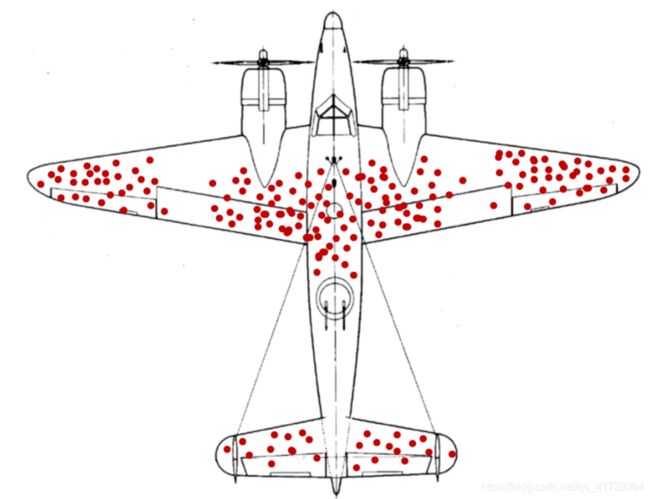
军方给数学家提供了很多数据。美军的飞机跟敌军的飞机交火之后返回基地,飞机上会留下来很多弹孔。军方发现,在返航的飞机上,机身上的弹孔比引擎上的弹孔更多。
因此,军方认为,最应该加强防御的是飞机的机身。他们想让统计学家研究一下,为了保护飞机,机身需要增加多少装甲。
瓦尔德给出的答案却和军方最初的想法大不一样。瓦尔德认为,需要加装装甲的地方不应该是弹孔多的部位,而应该是弹孔少的部位,也就是飞机的引擎。
为什么会是这样呢 ??
我们先从一个理论假设来看。从理论上来说,飞机各个部位中弹的概率应该是一样的。
那么,为什么返航的飞机机身上的弹孔比引擎上的弹孔更多呢 ??换言之,引擎上本来应该有的弹孔去哪里了 ??
瓦尔德认为,这是因为引擎被击中的飞机都坠毁了。回来的飞机,机身上尽管留下了很多弹孔,却仍然能够经得住打击,所以才能安全返航。打个比方来说,如果我们到战地医院去统计受伤的士兵,您会发现,腿部中弹的士兵肯定比脑部中弹的士兵要多。脑部中弹的士兵很少能够活下来,腿部中弹的士兵才有更大的概率存活。
数学家把这类现象称为 “幸存者偏差”,人们只看到幸存下来的,却没有看见已经失败和消亡的。
再举几个 “幸存者偏差” 的例子:
- 妈妈为什么不挑食 ?因为她买菜的时候已经挑过了。
- 吸烟有害健康,烟草公司会列举长寿的人里也有很多人吸烟的例子来证明吸烟也可以长寿 !大多数吸烟的人提前去逝了。
- 因为媒体报道的交通事故基本是飞机,所以我们感觉飞机很危险,事实是汽车每天出事的概率远大于飞机,报道的却少。
- 在股票的买卖上,很多骗局就是利用 幸存者偏差 骗到了投资人,原理就是:“大面积撒网,选择性补刀”。
- 比尔·盖茨、扎克伯格、脱不花 等人都没上完大学,那我们是不是就不要上大学了呢 ?您要知道和创业一样,媒体报道的都是成功的极小数,对于大部分人来说,大学并不一定可以提高成功的概率( luck ! ),但一定会减低您失败的概率。
现在,我们一起分析一下 幸存者偏差理论 的数学基础吧。
我们做一个简单的假设,飞机被击中的部位只有俩个,引擎和机翼,这两个随机事件分别被称之为 A 和 B。
当然还有一种情况,就是 A 和 B 同时发生,为了简单起见,我们不考虑 TA 。
于是飞机被击中的总概率为 P(A) + P(B)。
接下来如果 A 发生(击中引擎),坠落的概率我们假定为 P1,返航的概率当然就是 1 - P1。
类似的,我们假设 B 发生后(击中机翼),坠落和返航的概率为 P2 和 1 - P2。
由于有幸存者偏差,我们看到的坠毁和返航的分布情况是 P2 和 1 - P2,但这是一部分信息缺失的情况下的误判。
那么真实的坠毁和返航比例应该是什么呢 ? ?
在前面的假设下,飞机坠毁的总概率为 P(A) * P1 + P(B) * P2。
之前有说 飞机被击中的总概率为 P(A) + P(B),因此被击中后坠毁的 条件概率 可以用一个公式给出,当然返航的概率就是从 100% 中减去 TA 。
公式及推导:
我们假定引擎被击中的概率为 5%,被击中后坠毁的概率为 60%,机翼被击中的概率为 10%,被击中后坠毁的概率为 10%。
10% vs 90%,这是我们在缺失信息后看到的坠毁和返航的比例(击中机翼的情况,坠落和返航的概率为 P2 和 1 - P2)。
用上面的式子算下来,总的来讲飞机被击中后坠毁的概率为 27%,因此真实的返航坠毁比例是 27% vs 73%,而不是 10% vs 90%,说明信息缺失很多。
如果我们加固引擎,让击中后坠毁的概率降到 30%,减少机翼的装甲,让相应的概率增加到 15%,那么总的来讲飞机被击中后坠毁的概率降低到了 20%,比前面的 27% 降低了很多。
相反,如果加固机翼,减少引擎的装甲,被击中后坠毁的概率将大幅上升。
从哲学角度来说:幸存者偏差应是说,重要的东西要用心看。
It is only with the heart that one can see rightly; what is essential is invisible to the eyes.
---《小王子》
而学习哲学的这个动作,能帮您透过现实世界错综复杂的表面看清现象的本质。
丑小鸭定理
我,我长的丑怎么办 ?
《丑小鸭的故事》:
在夏日阴凉的树阴下,鸭妈妈孵着鸭宝宝。小鸭子一个个破壳而出,只有那只最大的蛋还没有动静。鸭妈妈耐心地等着,终于,小家伙钻出来了,他又大又丑,和别的小鸭子很不一样。大家一见到他就叫起来:瞧,他多丑啊!有一只鸭子马上扑过来,狠狠啄了他一下。
大家都不喜欢丑小鸭,连他的兄弟姐妹也说:“你这个丑八怪,真希望猫儿把你抓去才好!”
丑小鸭很难过,他真想躲到一个别人看不见的地方。这天天黑的时候,他悄悄地离开了家,晚上睡在一片沼泽地里。天亮时,突然传来砰砰的枪响,整群的大雁从芦苇里飞出来,原来有猎人在打猎。一只猎狗跑了过来,把鼻子顶到他身上,凶巴巴地露出牙齿。丑小鸭吓得缩成一团,可是猎狗嗅了嗅,又跑开了。
啊,我丑得连猎狗也不咬我了!丑小鸭悲伤地想。
他来到一家农舍,农舍里住着一只小猫和一只母鸡。母鸡问:“你会生蛋吗?”丑小鸭摇摇头。母鸡说:“这么重要的事你都不会做!”
小猫问:“你会拱背吗?会喵唔喵唔叫吗?”丑小鸭又摇摇头。 “那你会什么呢?”小猫轻蔑地问。丑小鸭想了想,说:“我会在水里游泳。”
母鸡和小猫哈哈大笑,他们都看不起丑小鸭。不久,丑小鸭离开了他们。
秋天来了,鸟儿们成群结队地飞往温暖的南方。一天,草丛中飞出一群白色的大鸟,细长的脖子,洁白的翅膀,他们是这样美丽,丑小鸭看得呆了,他真羡慕这些美丽幸福的鸟儿。
冬天的天气越来越冷,水结冰了,丑小鸭和冰块冻在了一起。幸好有个农夫把他带回了家。丑小鸭醒来后,有些害怕,他躲进厨房,可是不小心打翻了牛奶壶,牛奶泼了一地。农夫的妻子尖叫起来,丑小鸭吓坏了,看见大门敞开着,他赶紧逃出了农夫的家。
这个冬天寒冷又漫长,丑小鸭没有东西吃,也没有朋友,他艰难地捱着。当冬天过去,春天终于来临的时候,丑小鸭忍不住想大哭一场。
他拍拍翅膀,发现翅膀比以前有力得多,他试了两下,竟然可以飞起来了!他飞出沼泽,飞过森林,到了一个美丽的湖边。这时,他又看见了那群美丽的天鹅,正在水面上游来游去。他自惭形秽,把头低低地垂到水上,只等待着死。但是他在这清澈的水面上看到了什么呢?他看到了自己的倒影。但那不再是一只粗笨的、深灰色的、又丑又令人讨厌的鸭子,而却是——一只天鹅!许多大天鹅在他周围游泳,用嘴来亲他。他现在清楚地认识到幸福和美正在向他招手。
花园里来了几个小孩子,他们向水上抛来许多面包片和麦粒。最小的那个孩子喊道:“又来了一只新天鹅!”大家都说新来的天鹅最年轻、最好看。听到大家说他是美丽的鸟中最美丽的一只鸟,丑小鸭感到又难为情又幸福,它从内心里发出一个快乐的声音:“当我还是一只丑小鸭的时候,我做梦也没有想到会有这么多的幸福!”
丑小鸭不仅是一个故事,也是一个数学定理。
请问是俩只天鹅之间的差距大还是一只鸭子和一只天鹅的差距大 ?
大家基本都会认为鸭子和天鹅的差距大,因为俩只天鹅都是天鹅,种类是一样的。
这么想就只考虑了他们的外形,就像人分成了 高矮/颜值/经济/性格/健康 等等,每按一种标准考虑,人就被分类了。
天鹅和天鹅是相似的吧,比较差距主要看,您的标准是什么 ,但标准,可能有无数个。
名词解析
相似:所谓这俩个对象“相似”,就是在给所有对象分类的时候,这俩个对象能被分在同一个类里面。在各自不同的分类之中,TA们俩个被分到一起的次数,就是相似度的大小。
对象:
举个例子。
三个对象排成一排,分别是 天鹅A、天鹅B 和 丑小鸭。
我们来看看对这三只鸟有多少种分类方法,具体做法是我们选择一个属性,符合这个属性的就算是一类,不符合的就不算。
比如说,我们选择的属性是“白色”,那俩只天鹅是白色,丑小鸭是灰色的,所以根据这个属性,俩只天鹅就被选中,而丑小鸭不在这一类。
这个分类结果可以用 (110) 表示 —— 对应三个对象的位置,1 代表在这个分类里,0 代表不在这个分类里。
而如果我选择的属性是 “排第一名”,那就只有 天鹅A 在这个分类里面,分类结果就是(100)。
如果属性是 “不是白色”,那俩只天鹅都不算,只有丑小鸭在这个分类里面,结果就是(001)。
如果属性是 “白色,但是不排第一名”,结果就是(010)。
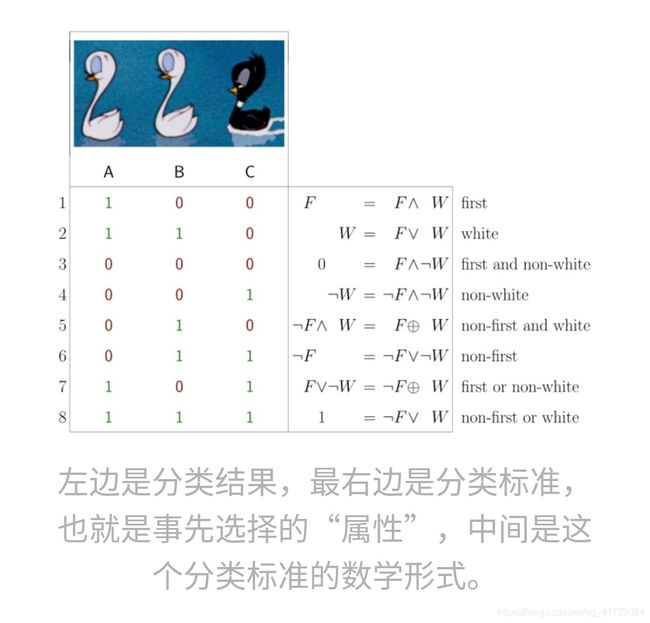
以此类推......发现,对下面图中表示的八种分类方法,其实都能找到一个对应的“属性” ——
而且对于三个物体,一共也就只有这 8 种分类方式。
那怎么定义相似度呢 ?
就是看这 8 种分类之中,有多少种,这俩个对象被分到了同一类。比如说 天鹅A 和 丑小鸭,就在(101)、(111)、(000)、(010) 这四个分类中属于同一类,那我们就可以说 天鹅A 和 丑小鸭 的相似度 = 4。
同理,天鹅B 和 丑小鸭 的相似度也是 4。
而 天鹅A 和 天鹅B 的相似度 ??
TA们同类的分组是(110)、(111)、(000)、(001),也是 4。
也就是说,丑小鸭 和 天鹅 之间的相似度,和俩只天鹅之间的相似度,是一样的。
这就是 “丑小鸭定理”。
一般来说,如果有 N 个对象,那么您就一共有 ![]() 次方种不同的分类方法,而结果还是这样,各个对象之间的相似度是一样的。
次方种不同的分类方法,而结果还是这样,各个对象之间的相似度是一样的。
换一个说法,丑小鸭定理也可以表述成:“丑小鸭跟天鹅之间的差异,和两只天鹅之间的差异一样大。”
正如世界上不是只有长的帅的,也还有长的让人放心的(即脸大或脸圆),所以别人才会找您倾述自己的生活啊。
在计算机里有一个模式识别,功能是让算法自动的客观分类给定的所有对象。
学过丑小鸭定理的您,是否觉得这是一个能实现的算法 ??
这显然是不可能的,因为人给出的分类标准都是主观的,因此这个分类标准是不靠谱的。
应用这种分类,只会激起海啸、无尽的争论:
- 将人按照种族分,其实种族并不存在;
- 将人按照学历分,其实学历并不存在;
- 将人按照性别分,其实性别并不存在;
每一种分类都是主观的,每一种分类也可能是天生就带有 偏见 的,因为您先 “偏见” 了这个属性,您才会以这个属性来分类。
那么,只要分类就有偏见。
什么时候,使用分类呢 ?
想到了一个价值,分类才是值得的。
那如果没有价值,只是随便分类,就很有可能限制自己的认知,还可能无形地伤害别人。
丑小鸭 和 任何一只天鹅 没有本质区别。
多想想这个定理,您可能会变成一个心胸更宽广的人。
从哲学角度来说:丑小鸭定理是说,一切分类都是主观的;有分类就会有歧视,但不分类就没那么好的效率,此事古难全。
阿姆达尔法则
IT 行业为什么发展是如此神速 ?
1999年,比尔·盖茨在世界计算机展上讲,如果汽车工业能够有IT产业的发展速度,那么一加仑(大约四升)汽油应该能让汽车跑1000英里,而且汽车的售价只要25美元。
世界上真有一个法则和一个定律,能解释这个现象。
阿姆达尔法则,是让 IT 行业得以快速进步的战术,和 TA 相对应的是摩尔定律,这是 IT 行业的战略。
阿姆达尔在设计计算机系统时,充分认识到了计算机各部分的性能必须平衡匹配,才能得到整体性能最佳的系统。
他将这种思想用一个简单的公式描述出来:
- 方程左边的 S :系统最后的性能提升
- 方程右边的 s :某一项指标的性能提升(如内存速度提高 1 倍,s 就是 1 倍)
- 方程右边的 p :这项提升被用到的比例/概率(如内存的读写访问,占程序运行时间的 20%)
假设内存的速度翻一番,即 s=2,那整个计算机性能的提升是多少呢 ?
根据这个公式,可以算出是 11%,这个结果看起来还是不错的,如果您有办法将内存的速度提升到原来的 100 倍,那么计算机整体速度只能提升约 25%,这看上去就不大有效了。
在每一次设计新的一代计算机产品时,都会有各种各样的技术突破,可供选用,但是考虑到成本的因素,以及设计的复杂度,都需要有所取舍,那么该引入哪些新技术呢 ?
阿姆达尔法则是计算机行业作决定的铁律。
假如内存读写占用程序运行时间的 20%,处理器运算占 60%。
现在有两个技术,一个可以将内存读写速度提高 5 倍,另一个可以将处理器的速度提升 50%,由于成本的限制和研发时间的限制,下一个版本只能采用一项改进,应该选用哪个 ?
20% 的 5 倍,好像效果显著;而 60% 的 50%,也就 30%,所以当然应该采用新的内存技术。
阿姆达尔法则给出的结论,则恰恰相反 ---- 根据上述公式,提高内存的性能,计算机整体的性能只能提高20%( 1/[(1-0.2)+0.2/6]≈120% ),如果提高处理器的性能,系统整体的性能能够提高 25%( 1/[(1-0.6)+0.6/1.5] = 125% )。
接下来,如果一年后还要再推出一个新的系统,假定处理器和内存的性能提升的可能性和成本跟上一次相当,这回该改进计算机处理器,还是内存呢?
还是该改进处理器,很遗憾,这一次该改进内存了。
因为上一次处理器改进后,处理器运算占用的时间比例,也就是公式中的 p,就从 60% 下降到 50% 了,再改进处理器,油水就没有那么大了。
事实上,如果继续改进处理器,可以得到 20% 左右的性能提升,而改进内存这回能获得 25% 的性能提升。
不仅在计算机设计中阿姆达尔法则是铁律,在软件开发,调试软件性能时,负责任的工程师都要用这个铁律将能够提升明显性能的模块都优化一遍。在大型的计算机软件开发中,有一个叫做 Profile 的工具,可以模拟出软件中每一个功能模块占用资源的情况,这样把最占用资源的模块进行优化,很容易成倍提高性能。
阿姆达尔法则不仅是产品设计中选择技术的准则,更是整个计算机行业里决定研发投入依据的原则,也就是说,当前如果计算机系统中的哪个部分成为了拖后腿的瓶颈,就必须集中精力和经费解决相应的问题,这也就解释了为什么IT的关键技术似乎都在合适的时间获得突破的原因。
从哲学角度来说:
很多时候,我们都面临在限制要素中作选择的问题。
很多时候,我们总想全方位改进自己,但是人的精力和资源有限,因此在某一时刻,可能只能向一个方向努力。
很多人从直觉出发,觉得该补短板,另一些人则觉得,该把长板变得更长。
第一类人讲木桶理论,第二类人讲长板理论,每一类都有很多成功的例子,也有很多失败的教训。
于是很多人就不知道该用哪一个理论了。
事实上您今天学了阿姆达尔法则后,就很容易作决断了,那就是在任何时刻算出 S,而后选收益最大的路径前进就好。
马尔可夫模型
想要一次性地采取一个行动去改变某件事,结果徒劳无功,我该怎么办 ?
不管您付出了多少努力,事情总会回到老样子,就好像冥冥之中有个无法摆脱的宿命一样。
上学时,我沉迷小说。班主任就找我谈话,要我戒掉;我也有决心......
比赛结束后,我跑步没上榜,决心下一年的比赛跑步一定要有名次......
在某个时候,下定决心要一直健身,改变自己......
可是,后来小说还是看、跑步水平也没高多少,健身也没坚持下来。
事情总会回到老样子,就好像冥冥之中有个无法摆脱的宿命一样。
数学模型能告诉您其中的原理,这个数学模型就是马尔可夫模型。
其实,这就是一个马尔可夫过程,满足马尔可夫过程有四个条件。
- 第一,系统中存在有限多个状态。
- 第二,状态之间切换的概率是固定的。
- 第三,系统要具有遍历性,也就是从任何一个状态出发,都能找到一条路线,切换到任何一个其他的状态。
- 第四,其中没有循环的情况,不能说几个状态形成闭环,把其他状态排斥在外。
举个例子,某位老师,发现课堂上总有学生无法集中注意力,会溜号。
所谓马尔可夫过程,就是假设学生在 “认真” 和 “溜号” 这两个状态之间的切换概率,是 固定的。
我们设定,今天认真听讲的学生,明天依旧认真的概率是 90%,还有 10% 的概率会溜号。
而今天溜号的学生,明天继续溜号的可能性是 70%,剩下 30% 的可能性会变得认真。
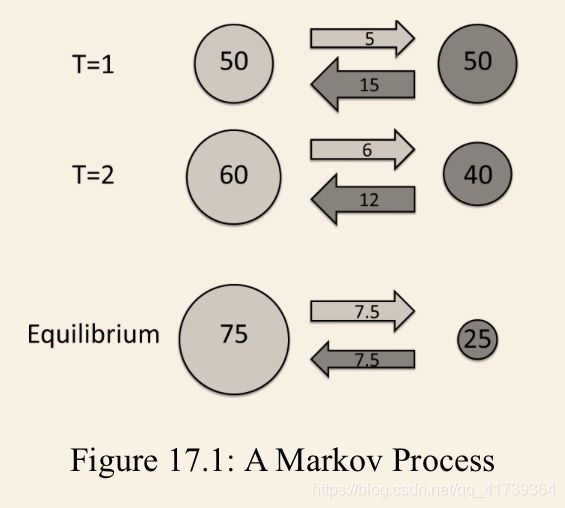
咱们看看这个模型怎么演化。假设总共有 100 个学生,第一天认真和溜号的各占一半。
- 第二天,根据概率的设定,50 个认真的学生中会有 5 人变成溜号;
- 而溜号的学生中,会有 15 人变成认真;
所以,第二天是有 60(50-5+15) 个人认真,剩下 40 个人溜号。
第三天,有 66 个认真的,34 个溜号的……
以此类推,最后有一天,您会发现有 75 个认真,25 个溜号的。
而到了这一步,模型就进入了一个稳定的状态,数字就不变了。
因为下一天会有 7.5 个学生从认真变成溜号,同时恰好有 7.5 个学生从溜号变成认真!
而老师对这个稳定态很不满意,为什么只有 75 个认真的呢 ?
TA 安排了一场无比精彩的公开课,还请了别的老师来帮 TA 监督学生。
这一天,100 个学生都是认真的。
但这样的干预对马尔可夫过程是无效的。
第二天认真的学生就变成了 90 个,第三天就变成了 84 个,……直到某一天,还是 75 个认真和 25 个溜号。
马尔可夫过程最重要的就是第二个过程,状态之间切换的概率是固定的 。
对应到人的身上,是人的习惯、环境、认知、本性等等影响的,只要是马尔可夫过程,不管 初始值/状态 如何,也不管在这个过程中有什么一次性的干预,ta 终究会演化到一个统计的 平衡态:其中每个状态所占的比例是不变的。
就好像终究会有 75% 的学生认真,25% 的学生溜号。马尔可夫过程,都有一个宿命般的结局。
从哲学角度来说: 马尔可夫模型就是:
- 如果您想改变一个人或一件事,授人以鱼不如授人以渔(改变概率)。
学者存在性定理
奥数怎解 ?
曾在《数学聊斋》里看到一个 抢 15 的游戏。
抢 15 是计算机科学家 西蒙 发明的,玩法是在 桌子上摆上 1、2、3、4、5、6、7、8、9 这九张牌,俩人轮流取牌,谁先拿到相加等于 15 的三张牌就获胜。
如果对方手里已经有 2 和 9,而您有1和7,现在该您走,您一定要拿 4,否则下一把对方拿 4 就赢了。
我们(和同班同学)经常会玩一些游戏:抢 15 、抢 30 、21 根火材、n 根火材、取石子 等等。
无论是哪一种游戏,如果您换个视角,游戏就会变得非常简单!
比如,抢 15 游戏中,您只要把这九个数字摆成一个九宫图,如下图所示:
抢 15 的游戏就变成了 井字棋,设法让自己占的三个格子连成直线,同时避免让对方连成。
只要您心中有这幅图,玩 15 游戏就会立于不败之地(当然,没有粗心的情况啊)。
名词解析:
视角:就是您 怎么看 这个对象,您把这个对象 看成什么。
譬如,这里有一大堆鱼,其中各种各样什么样的鱼都有,请问您怎么看这些鱼。 一个外行看这些鱼,可能会看到有的鱼大有的鱼小,或者看到有的是死的有的是活的。 渔民看这些鱼,可能考虑 ta 们的巡游地点,思考这些鱼是怎么捕捞来的。 市场上卖鱼的人看,他想的是哪个鱼贵哪个鱼便宜。而在您看来,可能想的就是哪个好吃哪个不好吃。
而数学定理中,恰好也有一个定理证明了:对任何一个问题,都存在一个能让答案一目了然、脱颖而出的视角。
一道难题摆在面前,可能当前谁都不知道怎么解决,但是您要相信,总有一个视角,会让答案看上去那么简单,能够脱颖而出。
- 这就好像以前的人认为光非常神秘,而牛顿一旦有了“光是不同颜色的混合”这个视角,光就不再神秘了。
- 以前的人觉得天体运行非常复杂,而牛顿一旦有了引力这个视角,他就能精准计算行星轨道。
视角,决定了问题的难度;也许普通人和大神差的只是一个视角及寻找视角的方法。
世界的规律在形式上并不复杂,但没有一个恰当的视角只会看得很复杂,因此寻找这视角反而是一个复杂的事情了。
奥卡姆剃刀法则
C语言的设计哲学:简单就是美。 为何简单就是美 ?
奥卡姆剃刀法则,又被称为 “简约之法则”。
文科、商科专业用 奥卡姆剃刀法则 解释 个人决策、社会现象、商业管理,理科、工科专业用 奥卡姆剃刀法则 来寻找理论模型......
从哲学角度来说: 奥卡姆剃刀法则 --- 能简单,就别复杂。
不知道您有没有看过一部讲述霍金生平的电影,叫《万物理论》,ta 的英文名叫 《The Theory of Everything》,字面意思就是 “能解释一切的理论”。 这个词并不是凭空杜撰的,从牛顿时代开始,物理学界就设想有一个能把所有物理学领域全都纳入其中,完整地统一起来的理论。 TA 相当于是物理学界的一座圣杯,包括霍金在内的几代物理学家都为之倾尽了毕生的心血,可至今都没有成功。
萨宾说(粒子物理学家):“想要用一种理论解释万物,这不就是源自于科学家们对 “简单性” 的追求吗” ?
既然大家都这么推崇这个法则,TA 是否有科学根据呢 ?
奥卡姆剃刀法则 与 信息论的关系,因为信息论就是建立在奥卡姆剃刀法则之上的。
在一个系统中,要消除不确定性,就要使用信息。
这个大方向没有错,那使用什么样的信息,使用多少信息合适呢 ??
我们不妨假定需要预测的目标是 Y,当然 TA 有不确定性,因此就有信息熵,我们写作 H(Y),是大于零的。
我们现在有一大堆信息,我们写作
。
这些信息可以帮助消除 Y 的不确定性。
我们不妨假定如果这些信息都用上,那所有的不确定性就消除了,也就是说在
的条件下 Y 的不确定性降为了 0 (即 H(Y|
)=0 )。
现在问题来了:真的需要那么多信息么 ??
显然不是,因为总有信息不那么有用,甚至是无效信息,那就一定存在一个很小的集合,比如
和
,我们用了这一点点信息就足够了。
也就是说 Y 在给定
,
条件下的熵,等同于 TA 在给定所有条件下的熵。
又有一个问题就了:怎样找到一个最小的集合 ??
对于这个问题,其实数学上是有答案的,就是找到一组所谓的基函数,傅里叶变换、正弦或者余弦函数就是基函数。
在计算机科学中,对于一个复杂的联络图,或者网络来说,就是找到一个所谓的最小支撑树。
大家不用记这些名词,只要记住在任何领域,都有这种成为支撑点的关键信息,找到 TA们并且使用 TA们,一切问题就可以迎刃而解,掌握和利用这些支撑点,就如同用剃刀剔除树的枝叶,把多余的枝枝蔓蔓,使我们困惑的信息去掉。
奥卡姆剃刀法则不仅有科学根据,在实践中也被不断地验证。
从哲学角度来说: 奥卡姆剃刀法则即 --- 能简单,就别复杂。
柯尔莫哥洛夫复杂度
人的追求有意义吗 ?
金庸 的作品:《笑傲江湖》、《天龙八部》、《鹿鼎记》。
香农定义信息的方法是看 ta “克服了多少不确定性”。
研究一部作品,香农的视角是基于概率论的,只看单个字出现的概率,不关心整个作品是什么“意思”。
而柯尔莫哥洛夫的视角,是您能用多短的语句去描写这部作品,正如上文的书评。
如何用最少的书评,才能让读者充分领会这部作品呢。
......
因为如果找到了这部作品的概括,您也就找到了这部作品的意义。
一些作品可能一句话就能概括,而一些作品却需要几页纸,对于如此不同的差距,我们也可以定义一个复杂度。
这个复杂度即 “柯尔莫哥洛夫复杂度”,复杂度是一个衡量一部作品概括难度系数的指标。
在计算机里,复杂度也分好几种情况,如 最好、最坏、平均 的;在概括一部作品里,复杂度同样也可分为 最长、最短、平均 的。
而 柯尔莫哥洛夫复杂度 是寻找概括这部作品最短的长度。
请问:“寻找某部作品的柯尔莫哥洛夫复杂度有什么意义吗” ??
“复杂” 真是一个非常 、非常 、非常 ...... 复杂的话题。
当今的人们还没找到一个公认的 “复杂” 的定义,但我们提出的 柯尔莫哥洛夫复杂度 却可以作为一个参考标准。
我们专注于作品的主干(抛开人物、对话、身外之物的具体细节),大概可以说:“俗套的作品” 的柯尔莫哥洛夫复杂度会较低,“不俗套的作品” 的柯尔莫哥洛夫复杂度会较高,而 “低” 和 “高” 取决于您能用多短的书评来概括这部作品。
像 数学家、哲学家、物理学家、社会学家等等 写的作品,如果只是概括一下就很简洁。
- 一个公式,如 1 + 1 = 2 ;
- 一句话,如 大道至简;
- 一句话,世界是能量的;
- 一句话,非零和游戏;
可这样的公式和话,本身就是一个作品,读者也不会理解。
因此,如果要满足让读者充分领会这部作品,那 TA 的柯尔莫哥洛夫复杂度会比一般的文学作品的柯尔莫哥洛夫复杂度高出许多,这样人们就可以根据柯尔莫哥洛夫复杂度来挑选作品了。
那我们能不能开发一个算法,自动判断每部作品的柯尔莫哥洛夫复杂度呢 ??
我们知道算法是可计算的,能不能开发这样的算法,只需要让计算机科学家来证明柯尔莫哥洛夫复杂度是可计算问题,还是不可计算问题,如果是可计算问题,这个算法就能实现。
后来,计算机科学家证明了这个定理哦,呃呃,TA 是不可计算的。
因此,这样的算法是不能开发出来的。
这样也恰恰说明了,不管我们对一系列事件的规律(书评)怎么总结,我们提出了一个多么深刻的解释 --- 我们永远都不知道还有没有更好的总结和更深的解释。
- 人的追求有意义吗 ?
柯尔莫哥洛夫定理说,“越努力越幸运,自然幸福的概率也高了”。
从哲学角度来说:我们永远都有可能从生活中发掘出新的意义!
推荐一个不错的漫画,在看似枯燥的职业生涯中,找到自己的价值、快乐和使命:《蔑视虚无人生指导手册》。
哥德尔不完备定理
1. 自然语言(如汉语)能表达一切吗 ?
2. 编程语言为什么要弄那么多(如,C、C++、python) ?
3. 真正的 人工智能 能不能实现(即超越人的人工智能) ?
在20世纪初的时候,有些数学家就有一个野心,说我们能不能找到一个机械化的方法,能够从最基本的数学公理出发,自动证明所有的数学定理 !!
当时数学家重点考虑的是有关自然数的理论体系,如哥德巴赫猜想就是有关自然数的一个论断,那数学家说,有没有一个机械化的方法,自动判断哥德巴赫猜想到底正不正确(类似古人追求长生不老)。
如果这个方法找到了,那就没有后来的陈景润、也没有其他数学家什么事儿了,什么漂亮的证明都会被机械化方法无情碾压!
数学家们努力了一番,貌似也取得了一些进展,人们充满雄心壮志。
可是在 1931 年的一次会议上,一个25岁的年轻人,哥德尔,做了一个报告,说他证明了一个有关自然数公理系统的定理。
据说当时冯·诺依曼就在报告现场,冯·诺依曼听完哥德尔的报告之后说了一句话:“全完蛋啦(It’s all over)!”
哥德尔证明了,在自然数的公理系统中,不但数学家们想要的那种机械化的证明不存在 —— 而且对有些命题来说,连“证明”本身,都根本就不存在!
这就是 “哥德尔不完备性定理”。
这个定理说,只要自然数的公理系统只有 有限条公理,那么就一定存在一些命题,您既不能用这些公理证明 ta 是对的,也不能判断 ta 是错的。
举个例子,假设您作为新员工入职了一家公司。老板说我们是一家成熟的公司,一切行为都有章可循。这里有一本手册,您拿回去好好学习。以后不管遇到什么情况都要对照手册行动:手册说该做的您就做,手册说不该做的您就不做。
您一看这本手册非常厚,上面密密麻麻写了好几千条规定。老板非常得意。
要是哥德尔遇到这家公司,他马上就会告诉老板 —— 总会有一些行动是既属于公司的活动范畴,又是您这本手册无法判断 TA 是对是错的!
也就是自然数的公理系统是 不完备 的,在自然数这个领域,您真的不能从几条有限的公理出发,推导出这个大厦,在自然数这个世界里,永远有新的东西等着我们。
也就是说,这种机械化的方法在自然数这个领域搞不成啊,顿时,数学家的整个世界观都崩塌了。
另外,哥德尔不完备性定理除了对自然数公理系统有效之外,对所有可数系统都有效。
像上面的员工手册、自然语言、计算机系统、算法,这些都在 哥德尔不完备性定理 的范围内,因为像自然语言、编程语言甚至是计算机系统,都是可数的,因为语言有界限,像计算机系统的 0 和 1 啊,无论是二进制还是十进制(任何进制都是等价的),所能表达的信息一定是有限的,这是信息编码本身就决定的。
在这样一个封闭系统中,总有一些语句是这个系统本身所无法判断对错的。
哥德尔不完备性定理答问题一:自然语言(如汉语)能表达一切吗 ?
因为自然语言是一个可数的系统,自然语言(如汉语)是不能表达一切的,如果您会双语就会感受到另一个语言的美丽,恰如西方的诗同样很美呢。
多学一门语言,就能跳出之前语言的局限性,只会一门语言局限就会比较大了。
哥德尔不完备性定理答问题二:编程语言为什么要弄那么多(如,C、C++、python) ?
虽然编程语言也是一个可数系统,但随着计算机行业的发展,创意十足。
为了通过开发效率,人们不再使用汇编语言,改为 C语言;为了满足开发大型项目的需求,人们创造了面向对象的思想,改用 C++ 等面向对象的语言,为了实现跨平台,改用 java 语言,编程总会遇到无法用当前的条件解决,这时候就会开发出新的产品来应对......
哥德尔不完备性定理答问题三:真正的 人工智能 能不能实现(即超越人的人工智能) ?
这就要看俩点了:
- 人脑是可数系统,还是不可数系统呢 ?
- 未来发明的机器是否是开关网络之外呢 ?
首先,人脑如果是可数的,那计算机很可能可以超越!!
如果我们的大脑都是计算机,那迟早有一天,我们会发现对这个系统我们能想明白的东西都已经想明白了,剩下的都是永远都不可能想明白的。
现在也没有人,能充分证明人脑不是图灵机。额,您要知道哦,一个可数的系统是证明不了自己的。
如果我们的大脑不是可数的,那我们可以不断地跳出旧系统,探索新知识、发明新语言,建立新系统。科学家永远可以琢磨新的物理定律,艺术家永远可以创造新的意境,工程师永远可以发明新的模型。
如果人脑是可数的,而未来发明的机器不是 开关网络 和 图灵机,超越人类,指日可待。
维特根斯坦的《逻辑哲学导论》说总会有一些语句,用这个语言系统本身是无法判断其对错的,对于这些东西,我们称之为不可说的,那对于不可说的,我们保持沉默,但这里的沉默其实是利用语言之外的东西让 ta 自己显现,也就是意会!
从哲学角度来说:哥德尔不完备性定理说的就是 纸短情长。
二进制编码的有效性
文言文为何如此简洁 ?
舍友看我再学计算机,于是说了一个题目来考考我。
有 64 瓶药,其中 63 瓶是无毒的,1 瓶是有毒的。
如果做实验的小白鼠喝了有毒的药,3天后会死掉,当然喝了其 ta 的药,包括同时喝几种就没事。
现在只剩下 3 天时间,请问最少需要多少只小白鼠才能试出哪瓶药有毒 ???
: 64 只。
每一只吃一种不同的药,这个答案只是在脑袋里过了一下。
一舍友说:“64 只太多了,对小白鼠不好”。
有 64 瓶药,其中 63 瓶是无毒的,1 瓶是有毒的。即 64 选 1,也就是 ![]()
答案是 6 只,为啥这么简单,而且这么少 ??
这就归功于信息被度量化了,比如您用天平称重,需要在另一边摆放相应重量的砝码,那衡量信息的砝码是什么呢 ??
香农最大的贡献在于找到了这个“砝码”,也就是将信息的量化度量和不确定性联系起来。他给出一个度量信息量的基本单位,就是 “比特”。
具体参见:香农的论文《通讯中的数学原理》。
“比特” 是这样定义的:如果一个黑盒子中有 A 和 B 俩种可能性,ta们出现的概率相同,那么要搞清楚到底是 A 还是 B,所需要的信息量就是一比特。
如果我们对这个黑盒子有一点知识,知道 A 的概率比 B 大,那么解密 ta 们所需要的信息就不到 1 比特。
如四选一的选择题需要的信息量是多少比特 ??
四选一是需要 4 比特吧 ,NO ,其实是 2 比特。
顺序的查找答案,A 、B 、C 、D,耗费最长的比特是 4 比特(答案要么是最后一个,要么都不是)。
事实上,我们完全可以采用二分法,计算机里的二分法需要满足顺序条件,这里改为圈地(用几何表示出来就是一颗二叉树哦)。
即 A 和 B 一组,C 和 D 一组,查找 AB组,看答案在不在,如果在就查是 A、B 的哪一个,直接查是 C、D 的哪一个即可,2 次就能知道答案。
从信息编码的角度来说,解决小白鼠的问题, 6 只(比特) 就是理论上最少的。
用数字描述就是: 32 -> 16 -> 8 -> 4 -> 2 -> 1,如果用二叉树画出来会很清晰。
而信息编码包含所有进制,现在我们就思考一下,理论是最少的采用的是什么进制 ??
如果没猜错的话,应该是 二进制,因为这种对半对半分一看就是和 2 有关呀。
那么如何用 二进制 解决呢 ?
复习一下:
- 比特就是面临 二选一 的时候,俩个可能性 都一样的时候。
- N 选 1 ,消除不确定性需要的比特数是 log 以 2 为底的 N,即
 。
。
我们将这些药从 0~63 按照二进制编号,获得64个六位数的二进制编号,也就是从 000000 (6个零) 到111111 (6个一),每个二进制编号的最左边是第一位,最右边是第六位。
而后选六只小白鼠从左到右排开,和二进制的六位,从左到右地依次对应。
您可以试着一位一位竖着看,每只小白鼠负责一位。
从左边数第一个小白鼠吃对应的二进制是 1 的药,0 就不吃。
第一只 ? 依次吃第 32,33,34,……,63 号药。
第二只 ? 吃 16,17,……,31,48,49,……,63号药,等等。
最后一只 ? 吃 1,3,5,……,63 号药。
您可能注意到了,6 只小白鼠都吃了 63 号,是因为 63 对应的二进制编号是 6个1,所以 6 只都要吃。
吃完药之后三天,某些小白鼠可能死了,我们假定第1,2,6这三只小白鼠死了,剩下的活着。
这说明什么呢 ??
说明编号 110001 号药有问题,也就是在第 1,第 2,第 6 位上分别是 3 个 1,因为这三只小白鼠都吃了ta,而 3,4,5 这三只没死的小白鼠没有吃 ta (对应的位置为0)。
而 110001 对应十进制的 49,也就是说第 49 瓶药是毒药。
对于其 ta 的组合也是同样的,您可以自己随便假定哪几只小白鼠死了,看看哪瓶是毒药。
当然,还有一种情况,就是所有的小白鼠都没有死,那说明第 0 号药是毒药,因为其 ta 的药都吃过了,就这一瓶没有吃。
在编码系统中,任何进制都是等价的。
为什么呢,我们一起来证明。
假设我们要表达 100 个数字,按照现在进制的划分可以分为俩种。
- 100 以内的进制 和 100 以外的进制(含 100 进制)。
100 以外的进制是,想 100 个符号来代替 100 个数字;
100 以内的进制,以 10 进制举例吧。只需要 10 个数字即可( 0 - 9 );
- 我们从 100 个数里,挑一个,不确定性是 100 选 1,信息量就是
,结果是 6.65 比特。
如果采用 100 以外的进制,也是一个 100 选 1 的问题,所需比特恰好也是 6.65,1 个符号信息量是 6.65 ,因此编码长度为 1 。
如果采用 100 以内的进制,如 10 进制,因为只有 10 个符号,每个符号的信息量是 ![]() ,结果是 3.325 比特。
,结果是 3.325 比特。
但 100 选 1 需要 6.65 比特,10 进制的一位是表示不了,诶 ,3.325 * 2 = 6.65 了。
也就是说,10 进制可以通过组合来达到消除不确定性所需的信息量,神奇不。
再试一下二进制啦,二进制的每一个符号包含的信息量即 ![]() ,结果是 1 比特。
,结果是 1 比特。
因为 1 * 7 >= 6.65,也就是需要 7 个符号才能表示 100。
可见,对数字的各种编码其实是等价的,不同的只是编码的长度。
表示 一百 这个整数值:
- 十进制:100,就俩个符号而已。
- 二进制:1100100,共七个符号。
- 一百进制:©️,就一个符号,假设在一百进制中 等于一百。
编码长的(1100100),如 二进制 只有 0 和 1,很容易记,但编码长度就长了,而 100 以外的进制(含 100 进制) 编码长度[©️]较二进制很短[1100100],但需要记住的符号太多了,这些符号可不是像 10 进制有规律的组合,完完全全没有任何联系。
从哲学角度来说:编码的有效性即把话说清楚,让最佳值理论落实到工程里。
中心极限定理与三大分布模型
以模型的视角把三大分布(正态、对数正态、幂率)放在一起讲。
正态分布
首先人具有多样性,每个人都是不一样的,有自己的想法、判断和追求。这给对人的研究造成极大的困难,使得社会科学几乎不可能是一门精确的科学。
不过别担心。您的确很难预测 一个人 的行为,但是您可以在大体上判断 一群人 的行为。
这是为啥呢 ??
因为个体的差异可以互相抵消。比如您开个餐馆,具体到一个特定的人今天来不来您这吃饭,您很难判断 —— 但是您每天的顾客人数其实都差不多。有的人本来想来因为临时有事来不了,有的人本来没想来因为路过看到就来了,这种种的出入互相抵消了。
如果您的餐馆事业已经比较稳定了,您不会太担心顾客流量的波动。这种情况,就是正态分布。
假设您的餐馆平均每天有 100 个顾客,比较好的时候能到 115 人,比较差的时候也有 85 人,那么画出图来,就是下面这样的一条钟形曲线 ——
曲线的横坐标代表每天来的人数,纵坐标代表在(比如说)一个季度之中,来这么多人的时候有多少天。
图中标记了正态分布的两个重要概念:平均值(μ),和标准差(σ)。
对您这个餐馆来说,μ = 100,σ = 15,这意味着在 68% 的日子里,您的顾客人数会在 85 和 115 之间 —— 这叫 “一个标准差之内”。
横轴上距离平均值越远的地方越是极端事件,而那些事件的纵坐标大小则代表TA们发生的概率。
只要您知道餐馆人数符合正态分布,平均值和标准差就都可以用平时的流量数据统计出来。
有了平均值和标准差您就可以大致估算各种事件发生的概率:95%的事情都发生在两个标准差之内,99.7% 的事情发生在三个标准差之内;黑客说要找个美貌程度在两个标准差之外的女朋友,那就意味着她要比 97.5%的人都漂亮。
为什么餐馆人数满足正态分布?
并不是所有随机事件都满足正态分布。想要学会判断什么样的事件满足正态分布,您必须有一点数学感,您需要了解“中心极限定理”。
中心极限定理说,如果一个事件满足下面这些条件,TA的分布就是正态分布 ——
- 第一,TA是由多个 —— 至少 20 个 —— 随机变量 *相加* 的结果;
- 第二,这众多的随机变量是互相 “独立” 的;
- 第三,每个随机变量的方差都只有有限大;
- 第四,每个随机变量对结果都要有一定的贡献,否则如果只是其中几个起到决定性的作用,那也不能算“多”。
简单地说,关键要求有两个:“相加”和“独立” —— 凡是多个独立随机变量相加的事件,结果就会是正态分布。
您的餐馆顾客满足这些条件。每个顾客来不来吃饭都是他自己的决定,是独立的;而您计算的是今天总共来了多少人,是这些人的和。
直观地说,中心极限定理说的是每个人来不来可能波动很大,但是因为人多,整体上来多少人,波动就不会有那么大,所以满足正态分布。如果局面不满足这两个条件(相加和独立),结果会是怎样的呢 ??
那您就得做好准备迎接极端事件了。
对数正态分布
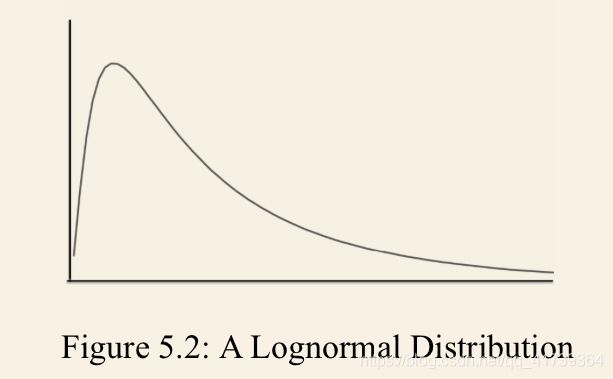
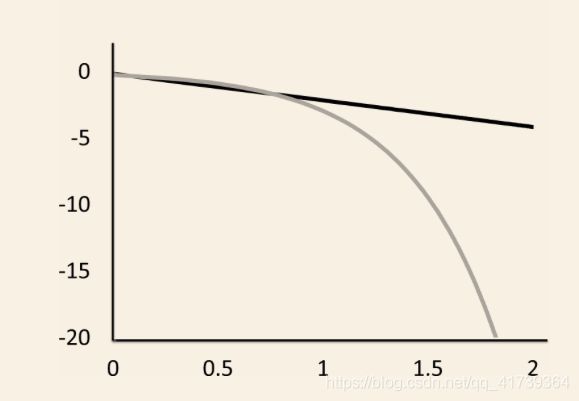
如果一个事件的结果不是由独立随机事件相加、而是由相乘决定的,它的分布将是“对数正态分布”。这个分布的形状就不是对称的钟形了,而是像下面这样 ——
它有一个比较长的尾巴,这意味着其中发生极端事件的可能性比正态分布高很多。
比如说涨工资吧。有个公司,本来员工之间工资相差不大。有一天老板宣布了一个涨工资计划,说以后每年业绩突出的员工,工资会增加 10%。您猜这个政策意味着什么?
意味着员工之间的工资差距将会变得越来越大。可能老王工资本来就比小李高,这次业绩又比小李好,那么老王涨 10%,小李没有,所以两人的差距将会变大。换一种情况,老王表现没有小李好,那么小李涨 10%,两人差距会缩小。但是,请注意,因为老王工资高,所以第一种情况导致的工资差距拉大,会超过第二种情况导致的工资差距缩小 —— 所以总体看来,全体员工的收入差距必然拉大。
这就是因为您使用了相乘的方法。换个方案,如果规定业绩好的员工,不论之前的工资是多少,一律涨一万块钱,那么员工之间的工资差距就不会拉大。
您喜欢让员工的收入差距拉大还是缩小呢?不管您喜欢哪种局面,您需要这个数学感。否则是您自己设计的模型,含着泪也得接受它的结果。
请注意,对数正态分布仍然假设每个随机变量的作用是互相独立的 —— 这意味着哪个员工今年能做出更好的业绩,跟他去年的工资没关系。而如果您认为员工工资代表了能力,那么工资越高的人就越有可能做出好业绩,那结果就不会是对数正态分布了,而是比这还要容易出极端事件的“幂率分布”。
幂率分布
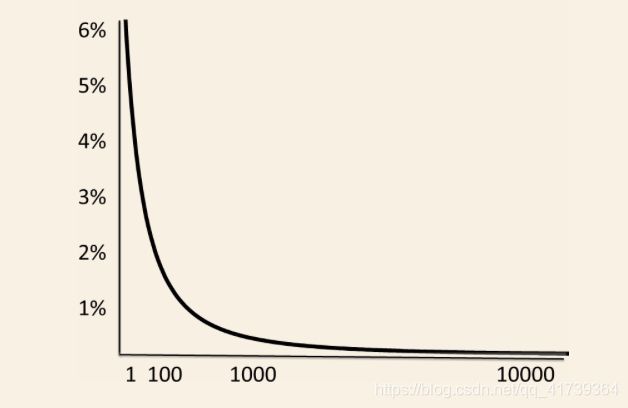
幂率分布的“长尾”,比对数正态分布更长 ——
这意味着幂率分布中会有大量的极端事件。
幂率分布是 不独立 的随机变量作用的结果。科学家找到了很多个能带来幂率分布的模型,咱们这里说其中最常见的两个。
第一个模型是“马太效应”。比如您去书店买书,那么多本书选哪本呢 ? 您会优先关注那些上了排行榜的“畅销书”。 这是人之常情,但是这对那些没上榜的书是不公平的 —— 这等于说越畅销的书就会越容易被关注,而越容易被关注就让它进一步更畅销。这就成了一个富者愈富的局面。
幂率分布使得图书市场中会出现少量特别畅销的书,而绝大多数书的销售成绩都很差。
而这一切都是因为您做决定的时候是在模仿别人。 您看到别人都买这本书,所以您才关注它。 您的买书行为不是独立的。
明星的粉丝数量、公司的大小、城市的大小,都是幂率分布。 比如一个城市越大,其中人与人的互动就越多,就业机会和创新机会也会越多,就越能吸引到新人的加入。 这就是为什么中国有那么多的超大城市。 当然每个幂率分布中的那个幂率参数不见得是一样的,但是这一讲我们不关心具体的数学,只关心数学感。如果一个局面中有很多极端事件,我们基本上可以猜测它满足某种某种幂率分布。 科学家做了个计算,说如果美国人的身高是幂率分布的,全美国就会至少有一个人比帝国大厦还要高,而且有一万人会比长颈鹿高……这就是幂率分布的威力。
另一种幂率分布模型来自于复杂系统的“自组织”现象。一个系统在变大、变复杂的过程中,它的各个部分互相依赖的程度将会增加。 到了一个临界点,因为互相关联实在太紧密了,一部分出个小问题就会导致整个系统出大问题,那就是雪崩式的灾难。
核电站的安全性、地震、森林大火,这些事情中包含自组织,各个部分之间会有复杂的联动。而我们说过,所谓蝴蝶效应,罪过不在蝴蝶,恰恰就是因为系统中的复杂联动。这些系统可能平时什么事儿都没有,但是其中蕴含着大灾难的可能性。
可能一个地区每天都发生一万次以上的小地震,影响微不足道,但是您考虑到地震是幂率分布的事件,就必须对大地震做好防灾准备。
总而言之,
如果这个事件代表多个独立随机变量之和,它就满足正态分布,您不用担心会有什么极端的情况发生。
如果一个事件是独立随机变量的乘积,那就是对数正态分布,其中会有一些比较极端、但不是那么极端的事情发生。
如果一个事件中的随机变量不是互相独立的,有互相模仿或者达成了紧密的关联,那您就必须做好应对极端情况的准备。
数学期望、标准差、正态分布
费马大定理、可证伪性、回归平均
回归平均
有这样一个故事,有一次 A 给以色列空军办讲座。
A 讲到心理学,对教官说,你要想让你的学员进步,一定要多正面鼓励,不要去骂他们。
心理学家有充分的证据,正面鼓励比打骂有效得多。
这时候有一个教官表示不同意,他跟 A 说,我的经验可不是这样的。
如果一个飞行员有一天飞得特别好,我当场表扬他、鼓励他了,他第二天往往飞得没有那么好。
可是如果一个人飞的特别差,我骂他一顿,他第二天果然就飞得没有那么差了。
这不就说明,表扬没用,打骂有用吗?
A 一时语塞!他后来才想明白这个事儿,这其实是回归平均。
飞得特别好这种事情并不容易发生,你表扬或者不表扬他,他下一次飞也会回归平均,会没有那么好。
飞得特别不好也是一个小概率事件,你批评或者不批评他,他下一次飞也会回归平均,会没有那么差。
在回归平均这个大趋势面前,表扬固然没有立竿见影的作用,批评的作用其实也是错觉。
有些事儿发生就发生了,并没有缘故。
从哲学角度来说:胜不骄,败不累 就是这么回事,一切都会回归平均。
除了回归平均之外,还有 复利思维、网络效应和马太效应、金字塔效应。
费马大定理
启发式、没有免费午餐定理、最小最大值定理
启发式
我最早听到“启发式”,是学习 NP 问题时,如旅行商问题。
这是一种算法,叫“启发式算法”。
启发式的英文是 "heuristic",启发式可以说是借鉴于生活中的例子来启发自己。
比如,您现在是大将军,您现在遇到困难了,这时也许您会翻一翻兵书,看看里面的三十六计。
最后,找到一个 “金蝉脱壳”,这个就是一个启发式的例子。
因此,启发式算法主要源于每个人的经验、之前的算法思想,启发法本质上就是向经验学习,拆解经验中的规律和套路为当下所用。
除此之外,启发式还有四种通用的套路:
- 类比启发式:通过联想寻找事物之间的联系和共同点,获取启发;
- 贪心启发式:通过寻找当前局面最优解,获取启发;
- 退火启发式:在贪心启发的基础上加上随机的探索,寻找到某个时刻时,停止探索,转为贪心启发式;
- 进化启发式:随机模拟生物(适者生存法则),留在最后的就是最优的;