数据结构与算法：查找

所谓查找(Search)又称检索，就是在一个数据元素集合中寻找满足某种条件的数据元素。查找在计算机数据处理中是经常使用的操作。查找算法的效率高低直接关系到应用系统的性能。查找的方法很多，本章将介绍一些常用的查找算法，主要有：线性表的查找、树表的查找和散列表的查找，并对有关的算法进行性能分析和对比

基本概念

1．数据表

就是指数据元素的有限集合。例如，为统计职工工作业绩，建立一个包括：职工编号、职工姓名、业绩等信息的表格。这个表格中的每一个职工的信息就是一个数据元素。对此表格可以根据职工编号查找职工的业绩等信息；也可以根据职工的姓名查找职工的业绩等信息。

2．关键字

数据表中数据元素一般有多个属性域（字段），即由多个数据成员组成，其中有一个属性域可用来区分元素，作为查找或排序的依据，该域即为关键字。每个数据表用哪个属性域作为关键字，要视具体的应用需要而定。即使是同一个表，在解决不同问题的场合也可能取不同的域做关键字。如果在数据表中各个元素的关键字互不相同，这种关键字即主关键字。

3．查找

查找(Search)是数据处理中最常用的一种运算。最常见的一种方式是事先给定一个值，在数据表中找到其关键字等于给定值的数据元素。查找的结果通常有两种可能：一种可能是查找成功，即找到关键字等于给定值的数据元素，这时作为查找结果，可报告该数据元素在数据表中的位置，还可进一步给出该数据元素的具体信息，后者在数据库技术中叫做检索；另一种可能是查找不成功（查找失败），即数据表中找不到其关键字等于给定值的数据元素，此时查找的结果可给出一个“空”记录或“空”指针。

4．静态查找表和动态查找表

数据表的组织有两种不同方式。其一，数据表的结构固定不变，当查找失败时，作为查找结果只报告一些信息，如失败标志、失败位置等，这类数据表称为静态查找表；其二，数据表的结构在插入或删除数据元素过程中会得到调整，当查找失败时，则把给定值的数据元素插入到数据表中，这类组织方式称为动态查找表。相比较而言，静态查找表的结构较为简单，操作较为方便，但查找的效率较低，而且需要考虑表的溢出问题。

5．查找的效率

查找是经常使用的一种运算，因此，查找的时间复杂度是人们关心的一个重要因素。查找的时间复杂度一般用平均查找长度（ASL）来衡量。平均查找长度是指在数据表中查找各数据元素所需进行的关键字比较次数的期望值，其数学定义为：

ASL=∑m=0nPi⋅Ci A S L = ∑ m = 0 n P i ⋅ C i

其中， Pi P i 表示待查找数据元素在数据表中出现的概率， Ci C i 表示查找此数据元素所需进行关键字的比较次数。

6．装载因子

设数据表的长度为m，表中数据元素个数为n，则数据表的装载因子 α=n/m α = n / m

顺序表的查找

采用顺序存储结构的数据表称为顺序表。顺序表适合作静态查找。

顺序表查找的基本思想是：设有n个数据元素的顺序表，从表的一端开始，用给定的值依次和表中各数据元素的关键字进行比较，若在表中找到某个数据元素的关键字和给定值相等，则查找成功，给出该数据元素在表中的位置；若查遍整个表，不存在关键字等于给定值的数据元素，则查找失败，给出失败信息。

索引顺序表查找

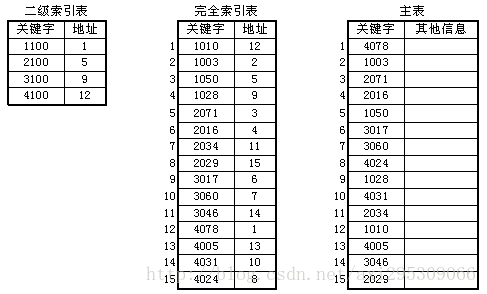
索引顺序表一般由主表和索引表两个部分组成，两者均采用顺序存储结构。主表中存放数据元素的全部信息，索引表中存放数据元素的主关键字和索引信息。一个学生信息的数据表如下图所示

二级索引图示

折半查找/二分查找

public static int binarySearch(int[] a, int key) {
    return binarySearch(a, 0, a.length, key);
}

private static int binarySearch(int[] a, int fromIndex, int toIndex, int key) {
    int low = fromIndex;
    int high = toIndex - 1;

    while (low <= high) {
        int mid = (low + high) >>> 1;
        int midVal = a[mid];

        if (midVal < key)
            low = mid + 1;
        else if (midVal > key)
            high = mid - 1;
        else
            return mid; // key found
    }
    return -(low + 1);  // key not found.
}

散列表查找

哈希表（散列表）：哈希表是通常的数组概念的推广。是一个元素为链表的数组，综合了数组和链表的好处（新华字典）。基于数组，数组创建后难于扩展。

哈希函数（散列函数）：根据关键字计算出位置（把关键字换成数组的下标），映射。使用哈希函数向数组插入数据后，这个数组就称为哈希表。

哈希算法，哈希值，哈希码，hashcode()
直接寻址
冲突（碰撞）：两个关键字可能哈希到相同的位置
填充序列，聚集

所谓查找实际上就是要确定关键字（Key）等于给定值（k）的数据元素的存储地址（Addr）。故查找问题本质上是确定关键字集合K到地址空间A的映射(即函数)：H：K -> A

因而，任何查找算法，都是计算函数H(k)的值的过程。

在前面介绍的查找算法中，由于k与H(k)之间没有简单直接的对应关系，函数H完全是一个隐式函数。因此，求H(k)值的时间不仅与数据表的存储结构有关，而且与数据表的大小n有关。

如果把函数H定义成简单的代数式，那么在查找时，只须计算H(k)之值，设H(k)=h，通过测试A[h]．key是否等于k(假定数组A表示存储空间)便可确定关键字为k的数据元素是否存在。这就能不经查找，在“一步”之内完成查找工作。

函数H把关键字转换成一个地址，因此这种存储技术称为键变换。又称杂凑(Hash)技术或散列技术。相应地，存储空间称为散列表，函数H称为杂凑(散列)函数。数据表的这种存储方式叫散列存储。

通过散列函数建立了从数据元素的关键字集合到散列表地址集合的一个映射。有了散列函数，就可以根据关键字确定数据元素在散列表中唯一的存放地址。

一般来说，散列函数是一个压缩映象函数。通常关键字集合比散列表地址集合大得多。因此有可能经过散列函数的计算，把不同的关键字映射到同一个散列地址上，这就产生了冲突。散列地址相同的不同关键字被称为同义词。

例如，有一组数据元素，其关键字分别是59、26、81，我们采用的散列函数是hash（k)＝k％11。其中，“％”是除法取余操作，则有：hash（59)=hash（26)=hash（81)=4。

对于散列方法，需要讨论以下两个问题：

• 对于给定的一个关键字集合，选择一个计算简单且地址分布比较均匀的散列函数，避免或尽量减少冲突
• 制订解决冲突的方案

散列函数

采用哈希函数的关键作用是减少需要被处理的数组大小。在构造散列函数时有几点需要加以注意：

• 其一、散列函数的定义域必须包括需要存储的全部数据元素的关键字，而如果散列表允许有m个地址时，其值域必须在0到m-1之间；
• 其二、散列函数计算出来的地址应能均匀分布在整个地址空间中，若key是从关键字集合中随机抽取的一个关键字，散列函数应能以同等概率取0到m-1中的每一个值；
• 其三、散列函数应是简单的，能在较短的时间内计算出结果。下面我们介绍几个散列函数。

1．直接定址法

此类函数取关键字的某个线性函数值作为散列地址：Hash（key）=a*key+c （其中a、c是整常数）

这类散列函数是一对一的映射，一般不会产生冲突，但是，它要求散列地址空间的大小与关键字集合的大小相同，这种要求是很苛刻的。特别是当关键字集合很大而且又不连续时，这种方法就不太适宜。

2．数字分析法

设数据表的长度为n，数据元素的关键字是一个d位数，关键字上每一位可能有r种不同的符号。这r种不同的符号在各位上出现的概率不一定相同，可能在某些位上分布均匀，出现的机会均等；在某些位上分布不均匀，只有某几种符号经常出现。数字分析法就是根据散列表的大小，在关键字中选取某些分布均匀的若干位作为散列地址。

3．除留余数法

设散列表地址空间大小为m，取一个不大于m，但最接近于或等于m的质数p，或者选取一个不含有小于20的质因数的合数作为除数，除留余数法的散列函数为：

Hash（key）=key % p （p≤m）

其中，“％”是整数除法取余运算，且p应避免取2的幂。

4．乘余取整法（乘法散列法）

使用此方法时，先让关键字key乘上一个常数a(0＜a＜1)，提取乘积的小数部分，然后再用整数n乘以这个值，对结果向下取整，把它作为散列地址

h(k)=m∗(kA−⌊kA⌋) h ( k ) = m ∗ ( k A − ⌊ k A ⌋ )

h(k) = ⌊m(kA mod 1)⌋

处理溢出的闭散列方法

为了解决冲突问题，需要对散列表加以改造。设散列表有m个地址，将其改为m个桶。其桶号与散列地址一一对应，第i(0≤i＜m )个桶的桶号即为第i个散列地址。每个桶可存放d个数据元素，这些数据元素的关键字应互为同义词。通常桶的大小d取得比较小，因此在桶内大多采用顺序查找。

处理溢出的一种常用的方法就是闭散列，也叫做开地址法。在这种方法中，所有的桶都直接放在散列表数组中，因此每个桶只存放一个数据元素(d＝1)。

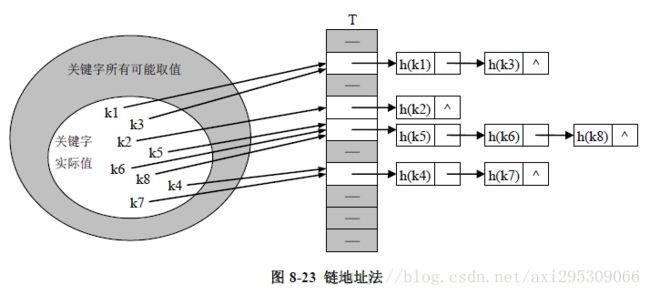
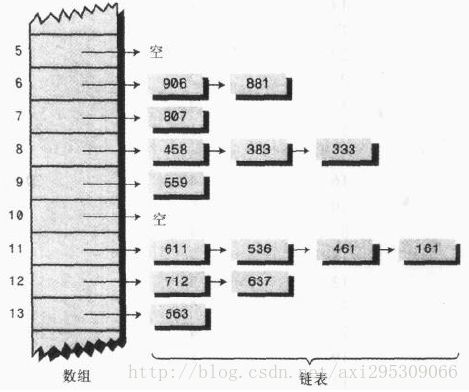
链地址法

数组 + 链表，把哈希到同一位置的所有元素都放到一个链表中，桶结构

创建一个存放单词链表的数组，数组内不直接存放单词，这样，当冲突发生时，新的数据项直接接到数组下标所指的链表中，这种方法叫做链地址法。

开放地址法

当冲突发生时，一个方法是通过系统的方法找到一个空位，并把这个单词填入，而不再用哈希函数得到数组的下标，这个方法叫做开放地址法

1、线性探测法

h(k,i)=(h(k)+i)modmi=0,1,2,3,...m−1 h ( k , i ) = ( h ( k ) + i ) m o d m i = 0 , 1 , 2 , 3 , . . . m − 1

2、二次探测法

h(k,i)=(h(k)+i2)modmi=0,1,2,3,...m−1 h ( k , i ) = ( h ( k ) + i 2 ) m o d m i = 0 , 1 , 2 , 3 , . . . m − 1

3、双散列法（双重散列）

h(k,i)=(h1(k)+ih2(k))modmi=0,1,2,3,...m−1 h ( k , i ) = ( h 1 ( k ) + i h 2 ( k ) ) m o d m i = 0 , 1 , 2 , 3 , . . . m − 1

扩展数组：当哈希表变得太满的时候，一个选择是扩展数组。在Java中，数组有固定的大小，而且不能扩展。编程时只能创建一个新的数组，然后把旧数组的所有内容插入到新的数组中。重新哈希化，原始聚集，二次聚集

再哈希法（二次哈希）、空间换时间

HashSet 的自动扩张

在数组满了之后，再要添加新项，就得先把数组扩张得大一些。显然，让新数组只比老数组多一个槽是不恰当的，因为那样岂不是以后每添加一个新项都得去扩张数组？那么应该创建多大的新数组才合适呢？目前通常的做法是让新数组比老数组大1倍。

另外，我们在前一篇已经提到过，开放寻址法在座位全部坐满的情况下性能并不好。上座率越低性能越好，但是也越浪费空间。这个上座率——也就是装载因子（_loadFactor）设为多少能达到性能与空间的平衡呢？.net framework 使用的是 0.72 这个经验值。

Android中使用的HashMap不是JDK中的HashMap，是Google重写了HashMap的代码，重写了hashCode()方法

java8后HashMap使用红黑树结构

HashMap内存泄露问题