数据结构-BST树(3)-bst的删除任意元素算法
文章目录
- 1.前言
- 2.bst树的删除操作
- 2.1.没有子节点
- 2.2.有一个子节点
- 2.3.有2个子节点
- 3.Demo
1.前言
通过上一篇的学习,我们知道bst树的插入操作和遍历等操作;
当我们按照如下顺序插入一堆数字时:
50;29;8;2;5;4;3;44;77;82;10;
呈现出来的树结构如下:
50
/ \
29 77
/ \ \
8 44 82
/ \
2 10
\
5
/
4
/
3
本文主要讨论bst树的删除;
那么接下来就以上面这个例子开始说吧;
2.bst树的删除操作
BST树删除一个节点分3种情况:
Q1:被删除节点是叶子节点(即没有左子树和右子树);
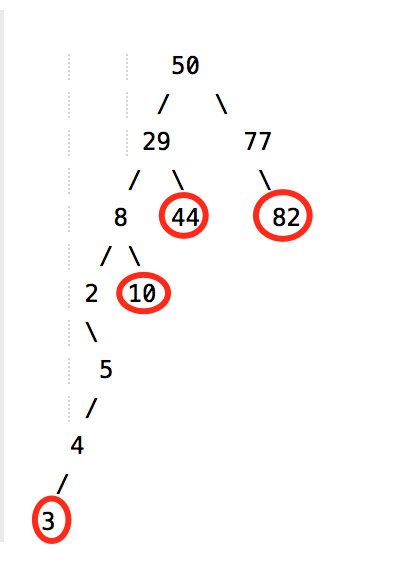
Q2:被删除节点不是叶子节点,且只有单个子树(左/右);

Q3:被删除节点不是叶子节点,且同时具有左右子树;

接下来对这三种情况进行深入分析;
2.1.没有子节点
最简单的一种情况,当被删除元素节点是叶子节点时,直接将该叶子节点与其父子关系解除即可;
代码:
if (srcNode.left == null && srcNode.right == null) {//叶子节点
if (srcNode.parent.left.value.compareTo(srcNode.value) == 0) {
srcNode.parent.left = null;
srcNode.parent = null;
return true;
} else if (srcNode.parent.right.value.compareTo(srcNode.value) == 0) {
srcNode.parent.right = null;
srcNode.parent = null;
return true;
}else {
System.out.println("异常:叶子节点情况");
}
}
测试结果(删除3):
Node{value=2__height=4, left=null, right=5, parent=8}
Node{value=4__height=2, left=null, right=null, parent=5}
Node{value=5__height=3, left=4, right=null, parent=2}
Node{value=8__height=6, left=2, right=10, parent=29}
Node{value=10__height=1, left=null, right=null, parent=8}
Node{value=29__height=8, left=8, right=44, parent=50}
Node{value=44__height=1, left=null, right=null, parent=29}
Node{value=50__height=8, left=29, right=77, parent=null}
Node{value=77__height=0, left=null, right=82, parent=50}
Node{value=82__height=0, left=null, right=null, parent=77}
50
/\
29 77
/\ \
8 44 82
/\
5 10
/
4
2.2.有一个子节点
删除只有单个孩子节点的元素时,只需要将其父节点指向其原本拥有单个孩子,并将其孩子的父节点指向为被删除元素的父节点即可。
一个不恰当的比喻,关系就像是剔除原本的“父亲”,由原本的“爷爷”元素和原本的“儿子”元素重新构成新的“父子”关系。
代码:
/**
* 处理节点删除
*
* @param srcNode 源节点,这个参数传进来的是
* @return
*/
private boolean handleDeleteNode(Node srcNode) {
if (srcNode.left == null && srcNode.right == null) {//叶子节点
......
} else if ((srcNode.left != null && srcNode.right == null) || (srcNode.left == null && srcNode.right != null)) {//瘸子子树
BinarySearchTree.Node tempValNode = null;
if (srcNode.left != null && srcNode.right == null) {//右瘸时
tempValNode = srcNode.left;
//判断当前删除节点是父节点的左或者右
if (srcNode.parent.left.value.compareTo(srcNode.value) == 0) {//如果当前待删除节点是其父节点的左节点时
srcNode.parent.left = tempValNode;
} else if (srcNode.parent.right.value.compareTo(srcNode.value) == 0) {//如果当前待删除节点是其父节点的右节点时
srcNode.parent.right = tempValNode;
} else {
System.out.println("异常:判断当前删除节点是父节点的左或者右");
}
} else if (srcNode.left == null && srcNode.right != null) {//左瘸时
tempValNode = srcNode.right;
if (srcNode.parent.left.value.compareTo(srcNode.value) == 0) {//如果当前待删除节点是其父节点的左节点时
srcNode.parent.left = tempValNode;
} else if (srcNode.parent.right.value.compareTo(srcNode.value) == 0) {//如果当前待删除节点是其父节点的右节点时
srcNode.parent.right = tempValNode;
} else {
System.out.println("异常:判断当前删除节点是父节点的左或者右");
}
} else {//异常
System.out.println("异常:瘸子子树情况");
return false;
}
if(null != tempValNode){
tempValNode.parent = srcNode.parent;
}else {
System.out.println("异常:瘸子子树情况:改变爷孙关系为父子关系");
return false;
}
} else if (srcNode.left != null && srcNode.right != null) {//左右子树都有
......
} else {//异常
System.out.println("异常:3种情况之外");
}
return true;
}
测试结果(中序遍历/删除元素2):
Node{value=3__height=1, left=null, right=null, parent=4}
Node{value=4__height=2, left=3, right=null, parent=5}
Node{value=5__height=3, left=4, right=null, parent=8}
Node{value=8__height=6, left=5, right=10, parent=29}
Node{value=10__height=1, left=null, right=null, parent=8}
Node{value=29__height=8, left=8, right=44, parent=50}
Node{value=44__height=1, left=null, right=null, parent=29}
Node{value=50__height=8, left=29, right=77, parent=null}
Node{value=77__height=0, left=null, right=82, parent=50}
Node{value=82__height=0, left=null, right=null, parent=77}
50
/\
29 77
/\ \
8 44 82
/\
5 10
/
4
/
3
测试结果:
Node{value=2__height=4, left=null, right=5, parent=8}
Node{value=3__height=1, left=null, right=null, parent=4}
Node{value=4__height=2, left=3, right=null, parent=5}
Node{value=5__height=3, left=4, right=null, parent=2}
Node{value=8__height=6, left=2, right=10, parent=29}
Node{value=10__height=1, left=null, right=null, parent=8}
Node{value=29__height=8, left=8, right=44, parent=50}
Node{value=44__height=1, left=null, right=null, parent=29}
Node{value=50__height=8, left=29, right=82, parent=null}
Node{value=82__height=0, left=null, right=null, parent=50}
50
/\
29 82
/\
8 44
/\
2 10
\
5
/
4
/
3
2.3.有2个子节点
终于进入删除节点的主菜了,我们先用一张图来说明当删除节点具备2个孩子时该怎么操作;
图中8是具有2个孩子的,要删除8该遵循什么操作呢?废话不多说,直接给出答案:
当删除当节点同时具备左右子树时,首先解除这个被删除节点当父子关系,然后用其中序遍历当后继节点进行补位替代其父子关系。
(如何找出后继节点在之前的文章里已经讲过)
这里就用直观的形式来观察:
2_3_4_5_8_10_29_44_50_77_82
8的后继节点是10,用其补位的结果就是下图所示:可以看出这也是一颗合法的bst树;
50
/\
29 82
/\
10 44
/
2
\
5
/
4
/
3
那么方法就出来了:
1.找出中序遍历下的当前待删除节点A的后继节点B
2.将B的value赋值给A
3.删除B
代码:
if (srcNode.left != null && srcNode.right != null) {//左右子树都有
//取出后继节点
BinarySearchTree.Node successorNode = getSuccessorNode(srcNode);
System.out.println(srcNode.value + " 后继节点: " + successorNode.value);
//1.值的替换
srcNode.value = (T) successorNode.value;
//2.置位空
if (successorNode.parent.left.value.compareTo(successorNode.value) == 0){//左
successorNode.parent.left = null;
}else {//右
successorNode.parent.right = null;
}
successorNode = null;
}
3.Demo
https://github.com/zj614android/designPattern/blob/master/app/src/main/java/com/zj/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84/%E6%A0%91/bst/BinarySearchTree.java



