论文学习-MobileNet-v1
文章目录
-
-
- 1、背景
- 2、深度可分离卷积
- 3.1、宽度缩放因子
- 3.2、分辨率缩放因子
- 4. 、代码分析
-
1、背景
卷积神经网络在计算机视觉任务中已经无处不在,并且总体趋势是向着更深更复杂的网络发展以获得更高的精度,但是这些所造成的是模型尺寸越来越大,速度越来越慢,很难在现实世界中获得实时的运用。作者提出的MobileNet可以构建小尺寸、低延时的模型,可以实现运行在嵌入式的移动视觉任务中。论文方案主要体现在两个方面。一个是深度可分离卷积,一个是宽度缩放因子和分辨率缩放因子两个模型超参数。
2、深度可分离卷积
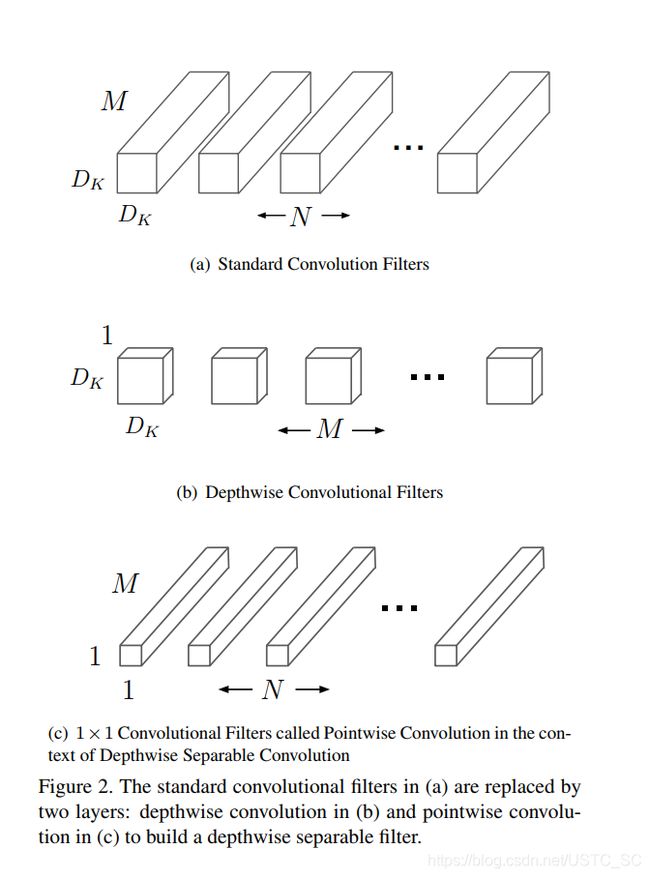
在MobileNet模型架构中核心部分就是深度可分离卷积。深度可分离卷积是将一个标准卷积分解成一个深度卷积层和一个1 * 1的卷积层(逐点卷积)。首先我们来看看标准卷积的功能是什么,对于一个输入,标准卷积的任务就是在一个步骤完成滤波并且合并输入特征图不同通道,产生一个新的输出特征图集合。而MobileNet的做法就是把这两个功能分开,用深度卷积完成滤波,逐点卷积完成通道数的合并。这样做的目的是在完成相同功能且不影响太多性能的同时,可以有效减少计算量与模型尺寸。接下来,我们通过一个示例来讲解一下。
对于一个输入特征图 F 尺寸为DF *DF * M,输出特征图G尺寸为DG *DG * N,其中DF 是输入特征图长(宽),M为通道数,DG 是输出特征图长(宽),N输出通道数。那么对于标准卷积卷积核K的尺寸就是Dk *Dk * M *N,Dk 是卷积核长宽。所以标准卷积对于这个操作的计算量是Dk *Dk * M * N * DF *DF 。为什么是这样呢,可以这么来理解,对于输入特征图来说,用每一个卷积核在一张特征图上计算量是 Dk *Dk * DF *DF ,那么对于M个通道来说就是 Dk *Dk * DF *DF *M,对于标准卷积来说是需要合并不同通道的,所以对于一个输出特征层的计算量是Dk *Dk * DF *DF *M,所以说对于N个输出特征层就是Dk *Dk * DF *DF *M *N。这部分结合下面的图更好理解。
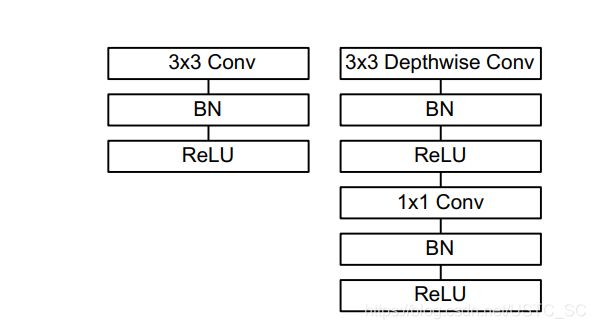
那么MobileNet是怎么做的呢?首先MobileNet先经过一个深度卷积,对于每一个特征层使用一个 Dk *Dk 的卷积核,这一步的操作所需要的计算量就是Dk *Dk * DF *DF *M,这个和标准卷积很像,不同的是,只在每个输入通道完成,没有合并通道创建新的特征图。然后经过的逐点卷积用1 * 1 的卷积产生 一个线性组合的深度层的输出,这一步的操作计算量是 DF *DF *M * N。同时这两步在每一步操作之后都接一个BN层和RELU线性激活。所以说对于深度可分离卷积所需要的计算量是 Dk *Dk * DF *DF *M + DF *DF *M * N,将深度可分离卷积与标准卷积比较如下

由以上公式可以看出,在MobileNet使用3 * 3 的卷积,计算相较于标准卷积少8-9倍,同时实验证明精度方面只有略微降低。下图展示标准卷积与深度可分离卷积的比较。
3.1、宽度缩放因子
基于前面介绍的深度可分离架构的MobileNet模型已经较小和低延迟了,但是很多时候一个特定的用例或应用程序可能要求模型更小和更快。为了构造这些更小更少计算开销的模型,作者引入了一个可调节的超参数α——宽度缩放因子(Width Multiplier )。理解起来也很简单,宽度缩放因子α在每一层均匀缩减网络,对于给定输入层的通道数为 M 变成 αM ,输出通道数为 N ,就变成了 αN,这样对于深度可分离网络的计算量就变成了Dk *Dk * DF *DF *αM + DF *DF *αM * αN,α的取值在(0-1)之间,比较典型的取值为 1 , 0.75,0.5 , 0.25.当α=1时就是标准深度可分离卷积。
3.2、分辨率缩放因子
作者提出的第二个超参数就是分辨率缩放因子(Resolution Multiplier ) β ,刚刚的宽度缩放因子针对于的是通道数,而分辨率缩放因子针对的就是特征图,具体就是通过分辨率缩放因子β改变输入图片大小,当输入图片尺寸改变,后面的特征图数量也都相应的改变了。β的取值也是在(0,1]之间,当等于1就是标准深度可分离卷积输入。
作者提出的两个超参数的作用就是给使用者在精度与延时上的一个权衡,在精度较高时,相对于延时就比较大;延时较小,参数较少,精度相对损失。我们也可以看看作者的实验结果,使用深度可分离卷积可以减少参数量而不太影响精度,以及一些宽度缩放因子与分辨率缩放因子的实验。
4. 、代码分析
以下为深度可分离卷积模块的pytorch简略版实现,可以看出还是比较简单的,深度卷积模块,不改变通道数,步长之类操作都在深度卷积模块完成,而通道数融合在逐点卷积这步完成,卷积核固定1*1,步长固定为1.
def conv_dw(self, in_channel, out_channel, stride):
return nn.Sequential(
#深度卷积
nn.Conv2d(in_channel, in_channel,
kernel_size=3, stride=stride, padding=1,
groups=in_channel, bias=False),
nn.BatchNorm2d(in_channel),
nn.ReLU(),
#逐点卷积
nn.Conv2d(in_channel, out_channel,
kernel_size=1, stride=1, padding=0,
bias=False),
nn.BatchNorm2d(out_channel),
nn.ReLU(),
)
BatchNorm2d(out_channel),
nn.ReLU(),
)