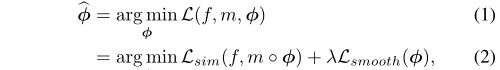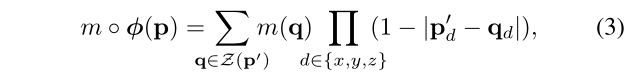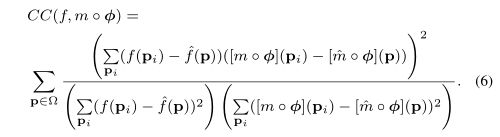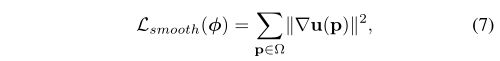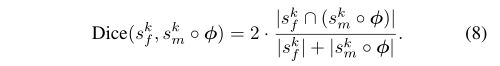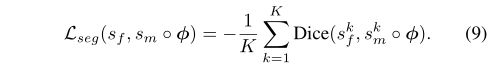VoxelMorph-2019

VoxelMorph-2019

Abstract

​ 本文提出了VoxelMorph，这是一个基于学习的快速可变形、成对医学图像配准框架。传统的配准方法为每对图像优化一个目标函数（objective function），对于大数据集或丰富的变形模型来说，这可能是耗时的。在最近基于学习的方法的基础上，本文将配准表示为将输入图像对映射（maps）到对准这些图像的变形场的函数。通过卷积神经网络(CNN)对函数进行参数化，并在一组图像上对神经网络的参数进行优化。给定一对新扫描后，VoxelMorph将通过直接计算函数来快速计算形变场（deformation field）。在这项工作中，探索了两种不同的培训策略（training strategies）。在第一个(无监督)设置中，本文训练模型以最大化基于图像强度(image intensities)的标准图像匹配目标函数(standard image matching objective function)。在第二个设置中，利用训练数据中可用的辅助细分（leverage auxiliary segmentations available）。

1. Introduction

​ 在传统非刚性配准中，在一对图像之间建立密集的非线性关系。传统的配准方法通过将外观相似的体素（voxel）对齐，同时对配准映射（registration mapping）施加约束（enforcing constraints）来解决每个体积对的优化问题(optimization problem)。但求解成对优化（pairwise optimization）可能需要大量的计算，速度很慢。

​ 本文提出了一种新的配准方法，该方法从体积集合（a collection of volume）中学习参数化的配准函数(parametrized registration function)。使用卷积神经网络(CNN)实现该功能，该网络采用两个n-D输入体，并输出一个体的所有体素(voxel)到另一个体的映射(mapping)。仅使用来自感兴趣的数据集中的体积的训练集（a training set of volumes）可以优化网络的参数，即卷积核权重。通过该集合体（collection of volumes）相同参数的共享，可以对齐来自相同分布（same distribution）的任何新的体积对。本质上是使用一个全局的代价函数（global function）来替代每个测试图像对传统配准算法昂贵优化（costly optimization of traditional registration algorithms for each test image pair）。

​ 在VoxelMorph框架中，可以自由地采用任何可微的目标函数(any differentiable objective function)。本文提出了两种方法，第一种方法称为Unsupervised2，仅使用输入卷对（input volume pair）和由模型计算的配准域（registration field computed by the model）。与传统的图像配准算法类似，该损失函数(loss function)量化了两幅图像的强度差异(the intensities of the two images)和变形的空间规律性(the spatial regularity of the deformation)。第二种方法还利用训练时可用于数据子集的解剖分段(leverage anatomical segmentations available at training time)来学习网络参数。

2. Background

​ 传统的配准流程（typical volume registration formulation），就是一个moving or source卷（volume）通过扭曲对齐（warped to align）到第二个fixed or target卷。非刚性配准把用于全局对齐的初始仿射变换（initial affine transformation）和具有更高自由度但慢得多的非刚性变换分开。

​ 传统的配准算法（registration algorithm）都是通过迭代最优化能量函数（energy function）实现变换的。最优化的函数如下：

​ f是fixed image，m是moving image，Φ是配准域（registration field）。m◦Φ是M使用形变场Φ配准后的图像。Lsim(.,.)用来衡量f和m◦Φ的相似性（similarity），Lsmooth(.)是对形变场Φ进行正则化（regularization），λ是正则化参数（regularization parameter）。

​ Φ、Lsim、Lsmooth有几个共同的形式。一般Φ通过移动向量场（displacement vector field）u来计算，Φ = Id + u，其中u是f图像到m图像每个voxel的矢量偏移量，Id是一个恒等变换。微分同胚变换（diffeomorphic transforms）将形变场Φ作为一个速度向量场的积分（integral of a velocity vector field），在变形中保持拓扑结构（topology）和可逆性（invertibility）。

​ Lsim的常用度量有灰度强度均方误差（intensity mean squared error）、交互信息（mutual information）和互相关（cross-correlation）。 交互信息（mutual information）和互相关（cross-correlation）在强度分布和对比度不一致时十分有效。

​ Lsmooth增强了一个空间平滑形变（spatially smooth deformation），一般是采用Φ空间梯度的线性操作（linear operator on spatial gradients of Φ）。通常为u的空间梯度的函数（function of the spatial gradients of u）。

​ 传统的算法对每对体进行优化，计算花费巨大。本文提出变换场可以通过一个参数化函数计算，在数据集上训练中这个函数。本质上这种共享参数的全局优化（global optimization of the shared parameters）来取代变换场的特定配对优化（pair-specific optimization of the deformation field），叫做“摊销”。

3. Related Work

A. Medical Image Registration(Non-learning-based)

​ 位移空间向量场的优化函数（optimize within the space of displacement vector fields）包括：

• 弹性模型（elastic-type models）

• 统计参数映射（statistical parametric mapping）

• b采样的自由度形式形变（free-form deformations with b-splines）

• 离散方法（discrete methods）

• Demons

​ 微分同胚变换（diffeomorphic transforms），可以保证拓扑结构（topology-preserving），并且在各种计算解剖学（computation anatomy studies）上取得了显著效果。常用的公式包括：

• Large Diffeomorphic Distance Metric Mapping(LDDMM)

• DARTEL

• diffeomorphic demons

• 标准对称归一化（Standard Symmetric Normalization(SyN)）。

B. Medical Image Registration(Learning-based)

​ 已经有一些论文提出了利用神经网络学习一个用于医学图像配准的函数，这些大多数依赖于扭曲域（warp fields）或者分割（segmentations）。这些提出的方法都是由一个CNN网络和空间变换函数（spatial transformation function）组成，但这些论文只是在3D子区域或者2D切片上做少量形变。还有一种方法提出了分割驱动的代价函数（segmentation driven cost function），本文实验时发现基于分段的损失（segmentation-based loss）对配准质量可能有帮助，基于图像和平滑度的损失（image-based and smoothness losses）也同样是必要的，特别是当我们评估训练过程中未观察到标签上的配准精度（registration accuracy）时，以及为了鼓励变形规律性（deformation regularity）。

C. 2D Image Alignment

​ 光流估计（optical flow estimation）是一个与二维图像配准相关的问题。光流算法（optical flow algorithms）返回一个描述二维图像对之间小位移的密集位移向量场（a dense dispalcement vertor field）。传统的光流方法使用变分方法（variational methods）解决类似于（1）的优化问题。拓展的方法可以更好地处理大位移或者外观显著变换包括基于特征匹配（feature-based matching）和最近邻域（nearest neighbor fields）的方法。近年来一些基于学习的神经网络光流估计（optical flow estimation using neural networks）的方法被提出。这些方法以图像对为输入，使用卷积神经网络学习图像特征（image features），从数据中捕捉光流的概念（capture the concept of optical flow from data），但是这个方法是需要监督标签的。

​ 空间变换层（the spatial transform layer）使得神经网络能够在不需要监督标签的情况下实现全局参数的2d图像对齐（global parametric 2D image alignment）和密集空间变换（dense spatial transformations）。

​ 以这些想法为基础，扩展空间变换器（extend the spatial transformer）以实现n-D体积配准，并进一步展示训练期间如何利用图像分割（leveraging image segmentations）来提高测试时的配准精度。

4. Method

​ F、M是定义在n-D空间的两个图像体（image volumes）。本文是在三维空间（n=3）且为了简化，假设F、M是单通道（single-channel）、灰度数据（grayscale parameters）。假定F、M在预处理阶段就已经仿射对齐（affinely aligned）了，仅剩下非线性对齐操作。有许多软件包可用于快速仿射对齐。

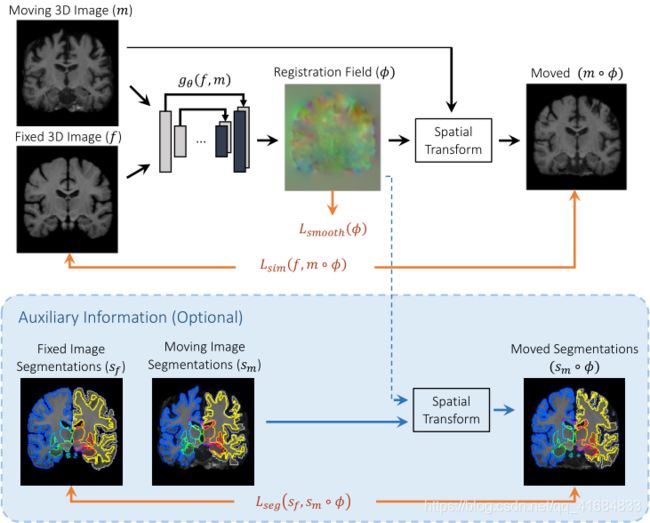
​ 本文使用卷积神经网络（CNN）建立函数gθ(f,m) = u，θ是网络参数（network parameters），即卷积核（the kernels of the convolutional layers）。位移场（displacement field）u通过一个n+1维图像保存。下图介绍了这种方法：

​ f和m作为输入，通过一组参数θ计算Φ（Φ = Id + u = Id + gθ(f,m)），通过空间变换函数（spatial transformation function）将m变换成m◦Φ，然后度量m◦Φ和f的相似性（evaluation of the similarity of m◦Φ and f）。

​ 使用（单元素）随机梯度下降法（(single-element) stochastic gradient descent）寻找最优参数θ。提出两种无监督损失函数（unsupervised loss functions），第一种方法获取图像的相似性（similarity）和场平滑度（field smoothness），第二种方法利用了解剖分割（anatomical segmentations）。

A. VoxelMorph CNN Architecture

​ g函数基于类似于UNet的卷积神经网络来实现参数化，网络由一些包含跳跃连接的编码器-解码器（encoder-decoder）组合而成。下图展示了VoxelMorph CNN的具体结构：

​ 将m和f组成一个2通道的3D图像，在本文实验中输入图像尺寸是160x192x224x2。在编码器和解码器阶段使用三维卷积，卷积核大小是3x3x3，步长为2。每个卷积层后接激活函数LeakyReLU，在卷积层获取输入图像对的层次特征（hierarchical features）获得相应的形变场Φ。

​ 在编码层（encoder）使用卷积步长（strided convolutions）来将空间维度减半，直到达到最小层。在输入图像的粗糙表示上随后的编码操作与传统的图像配准工作的图像金字塔（image pyramid）类似。

​ 在解码阶段（decoding stage）交替使用上采样（upsample）、卷积和连接跳跃（concatenating skip connections）。解码器的连续层在更精细的空间尺度上运行，从而实现精确的解剖对齐（anatomical alignment）。最小层的卷积核的接收域（receptive fields）应该至少与f和m中相应体素之间的最大预期位移相同（maximum expected displacement），最小层在输入图像大小的体积(1/16)3上卷积。

B. Spatial Transformation Function

​ 提出的方法通过最小化m◦Φ和f之间的差异（minimizing differences between m◦Φ and f）学习最佳参数。为了使用标准的基于梯度的方法（standard gradient-based methods），本文基于空间变换器网络（spatial transformer networks）构造了可微分（differentiable operation）的运算过程来计算m◦Φ。

​ 对于每个体素p，在m中计算（子像素）体素位置：p’=p+u( p)

​ 因为图像值仅能在整数位置，需要线性插值（linearly interpolate）在相邻的体素：

​ Z(p’)表示p’的领域体素（voxel neighbors of p’），d表示空间维度（dimensions of Ω）。这样就可以计算梯度（gradients）和二阶梯度（sub-gradients），可以在优化过程中进行误差反向传播（backpropagate errors）。

C. Loss Function

​ 本文提出两个损失函数：一个是无监督损失函数Lus（unsupervised loss function），另一个是辅助数据损失函数La（auxiliary data loss function）。

• 1) Unsupervised Loss Function：无监督损失函数Lus(.,.,.)由Lsim()和Lsmooth()组成。

​ 其中λ是正则化参数。实验中Lsim采用了两种方法。

​ 第一种是均方体素差（mean squared voxelwise difference），适用于f和m具有相似的图像强度分布和局部对比度时:

​ 第二种是f和m◦Φ的局部互相关（local cross-correlation），这种方法对于灰度变化有更好的鲁棒性，CC的公式如下，CC值越高说明对齐越好，得到损失函数：Lsim(f,m,Φ)=-CC(f,m◦Φ)

​ 其中，

​ 正则项为位移场u的梯度，梯度使用相邻体素的差值近似代替：

• 2) Auxiliary Data Loss Function：描述了VoxelMorph在训练阶段如何利用可获得的辅助信息（auxiliary information available）。在训练期间解剖分割图（anatomical segmentation map）可能是可获取的，由人工或算法进行注释，每个体素都归为一个解剖结构（anatomical structure）（每个体素都有一个解剖结构标签）。如果配准场Φ表示准确的解剖学对应关系，则f和m◦Φ中与同一解剖结构相对应的区域应很好的重叠（overlap well）。用骰子分数（Dice score）对这个重叠进行量化，其中sf，sm◦Φ分别为f和m◦Φ的结构k的体素：

​ 骰子分数为1表示解剖结构完全匹配，分数为0表示没有重叠。将所有结构k∈[1，K]上的分割损失Lseg定义为：

​ 结合Lus得到目标函数：

​ 由于解剖学标记的分类是明确的，因此单纯采用线性插值法（linear interpolation）来计算sm◦φ不合适，并且直接使用公式（8）可能使得框架无法自动化可微分（auto-differentiation）。将sf和sm设计成K个通道，每个通道是一个二值图像体（binary mask）对应一个解剖结构。然后对每个通道使用线性插值对sm进行空间变换，接着再计算公式（8）。

D. Amortized Optimization Interpretation

5. Experiments

A. Experimental Setup

• 1) Dataset
• 2) Evaluation Metrics
• 3) Baseline Methods
• 4) VoxelMorph Implementation

B. Atlas-based Registration

C. Regularization Analysis

D. Training Set Size and Instance-Specific Optimization

E. Manual Anatomical Delineations

F. Subject-to-Subject Registration

G. Registration with Auxiliary Data

• 1) Training with a subset of anatomical labels
• 2) Training with coarse labels
• 3) Regularity of Deformations
• 4) Testing on Manual Segmentation Maps

6. Discussion and Conclusion