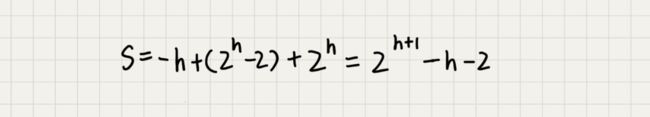数据结构与算法之美笔记 : 堆排序及应用
概念
只要满足这两点,它就是一个堆。
堆是一个完全二叉树;
堆中每一个节点的值都必须大于等于(或小于等于)其子树中每个节点的值。
第一点,堆必须是一个完全二叉树。还记得我们之前讲的完全二叉树的定义吗?完全二叉树要求,除了最后一层,其他层的节点个数都是满的,最后一层的节点都靠左排列。
第二点,堆中的每个节点的值必须大于等于(或者小于等于)其子树中每个节点的值。实际上,我们还可以换一种说法,堆中每个节点的值都大于等于(或者小于等于)其左右子节点的值。这两种表述是等价的。
对于每个节点的值都大于等于子树中每个节点值的堆,我们叫作“大顶堆”。
对于每个节点的值都小于等于子树中每个节点值的堆,我们叫作“小顶堆”。
如下图: 1,2 为 “大顶堆” 3,4 为“小顶堆”
堆 实现
用数组实现:
从图中我们可以看到,
数组中下标为 i 的节点的左子节点,就是下标为 i∗2 的节点,
右子节点就是下标为 i∗2+1 的节点,父节点就是下标为 i/2 的节点。
1. 往堆中插入一个元素
如果我们把新插入的元素放到堆的最后,你可以看我画的这个图,是不是不符合堆的特性了?
于是,我们就需要进行调整,让其重新满足堆的特性,这个过程我们起了一个名字,就叫作堆化(heapify)。
堆化实际上有两种,从下往上和从上往下。这里我先讲从下往上的堆化方法。
堆化非常简单,就是顺着节点所在的路径,向上或者向下,对比,然后交换。
我这里画了一张堆化的过程分解图。我们可以让新插入的节点与父节点对比大小。
如果不满足子节点小于等于父节点的大小关系,我们就互换两个节点。
一直重复这个过程,直到父子节点之间满足刚说的那种大小关系。
public class Heap {
private int[] a; // 数组,从下标 1 开始存储数据
private int n; // 堆可以存储的最大数据个数
private int count; // 堆中已经存储的数据个数
public Heap(int capacity) {
a = new int[capacity + 1];
n = capacity;
count = 0;
}
public void insert(int data) {
if (count >= n) return; // 堆满了
++count;
a[count] = data;
int i = count;
while (i/2 > 0 && a[i] > a[i/2]) { // 自下往上堆化
swap(a, i, i/2); // swap() 函数作用:交换下标为 i 和 i/2 的两个元素
i = i/2;
}
}
}
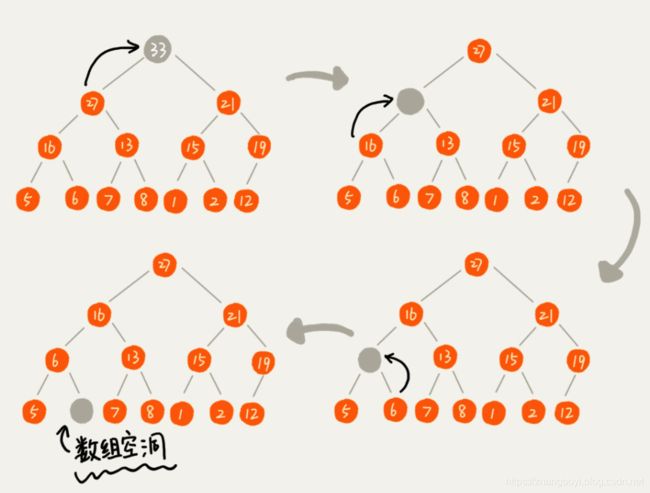
2. 删除堆顶元素
从堆的定义的第二条中,任何节点的值都大于等于(或小于等于)子树节点的值,
我们可以发现,堆顶元素存储的就是堆中数据的最大值或者最小值。
假设我们构造的是大顶堆,堆顶元素就是最大的元素。当我们删除堆顶元素之后,就需要把第二大的元素放到堆顶,那第二大元素肯定会出现在左右子节点中。然后我们再迭代地删除第二大节点,以此类推,直到叶子节点被删除。
这里我也画了一个分解图。不过这种方法有点问题,就是最后堆化出来的堆并不满足完全二叉树的特性。
实际上,我们稍微改变一下思路,就可以解决这个问题。
你看我画的下面这幅图。我们把最后一个节点放到堆顶,然后利用同样的父子节点对比方法。
对于不满足父子节点大小关系的,互换两个节点,并且重复进行这个过程,直到父子节点之间满足大小关系为止。
这就是从上往下的堆化方法。
因为我们移除的是数组中的最后一个元素,而在堆化的过程中,都是交换操作,
不会出现数组中的“空洞”,所以这种方法堆化之后的结果,肯定满足完全二叉树的特性。
public void removeMax() {
if (count == 0) return -1; // 堆中没有数据
a[1] = a[count];
--count;
heapify(a, count, 1);
}
private void heapify(int[] a, int n, int i) { // 自上往下堆化
while (true) {
int maxPos = i;
if (i*2 <= n && a[i] < a[i*2]) maxPos = i*2;
if (i*2+1 <= n && a[maxPos] < a[i*2+1]) maxPos = i*2+1;
if (maxPos == i) break;
swap(a, i, maxPos);
i = maxPos;
}
}
我们知道,一个包含 n 个节点的完全二叉树,树的高度不会超过 log2n 。
堆化的过程是顺着节点所在路径比较交换的,所以堆化的时间复杂度跟树的高度成正比,也就是 O(logn)。
插入数据和删除堆顶元素的主要逻辑就是堆化,所以,往堆中插入一个元素和删除堆顶元素的时间复杂度都是 O(logn)。
堆实现排序?
有时间复杂度是 O(n2) 的冒泡排序、插入排序、选择排序,
有时间复杂度是 O(nlogn) 的归并排序、快速排序,还有线性排序。
堆排序的时间复杂度非常稳定,是 O(nlogn),并且它还是原地排序算法。
堆排序的过程大致分解成两个大的步骤,建堆和排序。
1. 建堆
我们首先将数组原地建成一个堆。所谓“原地”就是,不借助另一个数组,就在原数组上操作。
建堆的过程,有两种思路。
第一种是借助我们前面讲的,在堆中插入一个元素的思路。
尽管数组中包含 n 个数据,但是我们可以假设,起初堆中只包含一个数据,就是下标为 1 的数据。
然后,我们调用前面讲的插入操作,将下标从 2 到 n 的数据依次插入到堆中。
这样我们就将包含 n 个数据的数组,组织成了堆。
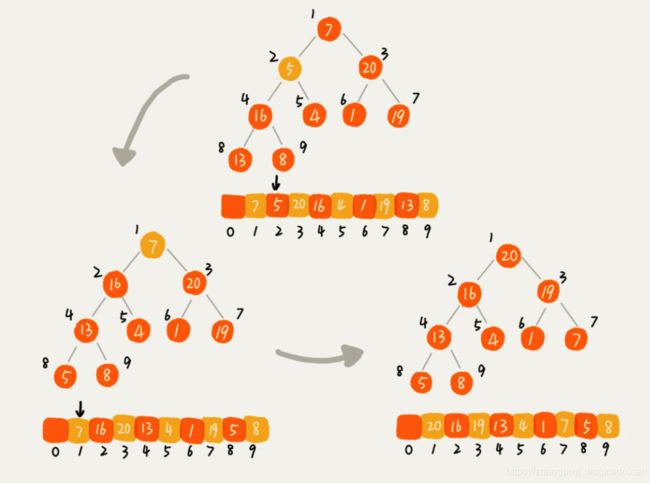
第二种实现思路,跟第一种截然相反,也是我这里要详细讲的。
第一种建堆思路的处理过程是从前往后处理数组数据,并且每个数据插入堆中时,都是从下往上堆化。
而第二种实现思路,是从后往前处理数组,并且每个数据都是从上往下堆化。
我举了一个例子,并且画了一个第二种实现思路的建堆分解步骤图,你可以看下。
因为叶子节点往下堆化只能自己跟自己比较,所以我们直接从第一个非叶子节点开始,依次堆化就行了。
private static void buildHeap(int[] a, int n) {
for (int i = n/2; i >= 1; --i) {
heapify(a, n, i);
}
}
private static void heapify(int[] a, int n, int i) {
while (true) {
int maxPos = i;
if (i*2 <= n && a[i] < a[i*2]) maxPos = i*2;
if (i*2+1 <= n && a[maxPos] < a[i*2+1]) maxPos = i*2+1;
if (maxPos == i) break;
swap(a, i, maxPos);
i = maxPos;
}
}
在这段代码中,我们对下标从 n2 开始到 1 的数据进行堆化,下标是 n/2+1到 n 的节点是叶子节点,我们不需要堆化。
实际上,对于完全二叉树来说,下标从 n/2+1 到 n的节点都是叶子节点。
每个节点堆化的时间复杂度是 O(logn),那 n/2+1 个节点堆化的总时间复杂度是不是就是 O(nlogn)呢?
这个答案虽然也没错,但是这个值还是不够精确。实际上,堆排序的建堆过程的时间复杂度是 O(n)。
我带你推导一下。
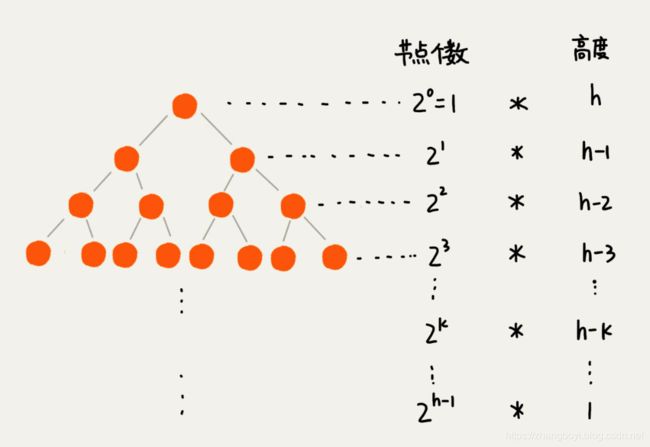
因为叶子节点不需要堆化,所以需要堆化的节点从倒数第二层开始。
每个节点堆化的过程中,需要比较和交换的节点个数,跟这个节点的高度 k 成正比。
我把每一层的节点个数和对应的高度画了出来,你可以看看。
我们只需要将每个节点的高度求和,得出的就是建堆的时间复杂度。
我们将每个非叶子节点的高度求和,就是下面这个公式:
这个公式的求解稍微有点技巧,不过我们高中应该都学过:把公式左右都乘以 2,就得到另一个公式 S2。
我们将 S2 错位对齐,并且用 S2 减去 S1,可以得到 S。
S 的中间部分是一个等比数列,所以最后可以用等比数列的求和公式来计算,最终的结果就是下面图中画的这个样子。
因为 h=log2n ,代入公式 S,就能得到 S=O(n) ,所以,建堆的时间复杂度就是 O(n)。
2. 排序
建堆结束之后,数组中的数据已经是按照大顶堆的特性来组织的。
数组中的第一个元素就是堆顶,也就是最大的元素。
我们把它跟最后一个元素交换,那最大元素就放到了下标为 n 的位置。
这个过程有点类似上面讲的“删除堆顶元素”的操作,当堆顶元素移除之后,
我们把下标为 n 的元素放到堆顶,然后再通过堆化的方法,将剩下的 n−1个元素重新构建成堆。
堆化完成之后,我们再取堆顶的元素,放到下标是 n−1n−1 的位置,一直重复这个过程,
直到最后堆中只剩下标为 1的一个元素,排序工作就完成了。
// n 表示数据的个数,数组 a 中的数据从下标 1 到 n 的位置。
public static void sort(int[] a, int n) {
buildHeap(a, n);
int k = n;
while (k > 1) {
swap(a, 1, k);
--k;
heapify(a, k, 1);
}
}
现在,我们再来分析一下堆排序的时间复杂度、空间复杂度以及稳定性。
整个堆排序的过程,都只需要极个别临时存储空间,所以堆排序是原地排序算法。
堆排序包括建堆和排序两个操作,建堆过程的时间复杂度是 O(n),
排序过程的时间复杂度是O(nlogn),所以,堆排序整体的时间复杂度是 O(nlogn)。
堆排序不是稳定的排序算法,因为在排序的过程,存在将堆的最后一个节点跟堆顶节点互换的操作,
所以就有可能改变值相同数据的原始相对顺序。
在前面的讲解以及代码中,我都假设,堆中的数据是从数组下标为 1 的位置开始存储。
那如果从 0 开始存储,实际上处理思路是没有任何变化的,唯一变化的,
可能就是,代码实现的时候,计算子节点和父节点的下标的公式改变了。
如果节点的下标是 i,那左子节点的下标就是 2∗i+1,右子节点的下标就是 2∗i+2,父节点的下标就是 i−1/2。
为什么快速排序要比堆排序性能好?
对于快速排序来说,数据是顺序访问的。
而对于堆排序来说,数据是跳着访问的。
比如,堆排序中,最重要的一个操作就是数据的堆化。
比如下面这个例子,对堆顶节点进行堆化,会依次访问数组下标是 1,2,4,81,2,4,8 的元素,而不是像快速排序那样,
局部顺序访问,所以,这样对 CPU 缓存是不友好的。
第二点,对于同样的数据,在排序过程中,堆排序算法的数据交换次数要多于快速排序。
我们在讲排序的时候,提过两个概念,有序度和逆序度。
对于基于比较的排序算法来说,整个排序过程就是由两个基本的操作组成的,比较和交换(或移动)。
快速排序数据交换的次数不会比逆序度多。
但是堆排序的第一步是建堆,建堆的过程会打乱数据原有的相对先后顺序,导致原数据的有序度降低。
比如,对于一组已经有序的数据来说,经过建堆之后,数据反而变得更无序了。
对于第二点,你可以自己做个试验看下。
我们用一个记录交换次数的变量,在代码中,每次交换的时候,我们就对这个变量加一,
排序完成之后,这个变量的值就是总的数据交换次数。
这样你就能很直观地理解我刚刚说的,堆排序比快速排序交换次数多。
应用
堆的应用一:优先级队列
首先,我们来看第一个应用场景:优先级队列。
优先级队列,顾名思义,它首先应该是一个队列。
我们前面讲过,队列最大的特性就是先进先出。
不过,在优先级队列中,数据的出队顺序不是先进先出,而是按照优先级来,优先级最高的,最先出队。
如何实现一个优先级队列呢?
方法有很多,但是用堆来实现是最直接、最高效的。
这是因为,堆和优先级队列非常相似。一个堆就可以看作一个优先级队列。
很多时候,它们只是概念上的区分而已。
往优先级队列中插入一个元素,就相当于往堆中插入一个元素;
从优先级队列中取出优先级最高的元素,就相当于取出堆顶元素。
你可别小看这个优先级队列,它的应用场景非常多。
我们后面要讲的很多数据结构和算法都要依赖它。
比如,赫夫曼编码、图的最短路径、最小生成树算法等等。
不仅如此,很多语言中,都提供了优先级队列的实现,比如,Java 的 PriorityQueue,C++ 的 priority_queue 等。
举两个具体的例子,让你感受一下优先级队列具体是怎么用的。
1. 合并有序小文件
假设我们有 100 个小文件,每个文件的大小是 100MB,每个文件中存储的都是有序的字符串。
我们希望将这些 100 个小文件合并成一个有序的大文件。
这里就会用到优先级队列。
整体思路有点像归并排序中的合并函数。
我们从这 100 个文件中,各取第一个字符串,放入数组中,然后比较大小,
把最小的那个字符串放入合并后的大文件中,并从数组中删除。
假设,这个最小的字符串来自于 13.txt 这个小文件,我们就再从这个小文件取下一个字符串,放到数组中,重新比较大小,并且选择最小的放入合并后的大文件,将它从数组中删除。
依次类推,直到所有的文件中的数据都放入到大文件为止。
这里我们用数组这种数据结构,来存储从小文件中取出来的字符串。
每次从数组中取最小字符串,都需要循环遍历整个数组,显然,这不是很高效。
有没有更加高效方法呢?
这里就可以用到优先级队列,也可以说是堆。
我们将从小文件中取出来的字符串放入到小顶堆中,那堆顶的元素,也就是优先级队列队首的元素,就是最小的字符串。
我们将这个字符串放入到大文件中,并将其从堆中删除。
然后再从小文件中取出下一个字符串,放入到堆中。
循环这个过程,就可以将 100 个小文件中的数据依次放入到大文件中。
2. 高性能定时器
假设我们有一个定时器,定时器中维护了很多定时任务,每个任务都设定了一个要触发执行的时间点。
定时器每过一个很小的单位时间(比如 1 秒),就扫描一遍任务,看是否有任务到达设定的执行时间。
如果到达了,就拿出来执行。
但是,这样每过 1 秒就扫描一遍任务列表的做法比较低效,主要原因有两点:
第一,任务的约定执行时间离当前时间可能还有很久,这样前面很多次扫描其实都是徒劳的;
第二,每次都要扫描整个任务列表,如果任务列表很大的话,势必会比较耗时。
针对这些问题,我们就可以用优先级队列来解决。我们按照任务设定的执行时间,将这些任务存储在优先级队列中,队列首部(也就是小顶堆的堆顶)存储的是最先执行的任务。
这样,定时器就不需要每隔 1 秒就扫描一遍任务列表了。
它拿队首任务的执行时间点,与当前时间点相减,得到一个时间间隔 T。
这个时间间隔 T 就是,从当前时间开始,需要等待多久,才会有第一个任务需要被执行。
这样,定时器就可以设定在 T 秒之后,再来执行任务。从当前时间点到(T-1)秒这段时间里,定时器都不需要做任何事情。
当 T 秒时间过去之后,定时器取优先级队列中队首的任务执行。然后再计算新的队首任务的执行时间点与当前时间点的差值,把这个值作为定时器执行下一个任务需要等待的时间。
这样,定时器既不用间隔 1 秒就轮询一次,也不用遍历整个任务列表,性能也就提高了。
堆的应用二:利用堆求 Top K
刚刚我们学习了优先级队列,我们现在来看,堆的另外一个非常重要的应用场景,那就是“求 Top K 问题”。
我把这种求 Top K 的问题抽象成两类。
一类是针对静态数据集合,也就是说数据集合事先确定,不会再变。
另一类是针对动态数据集合,也就是说数据集合事先并不确定,有数据动态地加入到集合中。
针对静态数据,如何在一个包含 n 个数据的数组中,查找前 K 大数据呢?
我们可以维护一个大小为 K 的小顶堆,顺序遍历数组,从数组中取出数据与堆顶元素比较。
如果比堆顶元素大,我们就把堆顶元素删除,并且将这个元素插入到堆中;
如果比堆顶元素小,则不做处理,继续遍历数组。
这样等数组中的数据都遍历完之后,堆中的数据就是前 K 大数据了。
遍历数组需要 O(n) 的时间复杂度,一次堆化操作需要 O(logK) 的时间复杂度,
所以最坏情况下,n 个元素都入堆一次,时间复杂度就是 O(nlogK)。
针对动态数据求得 Top K 就是实时 Top K。怎么理解呢?
我举一个例子。一个数据集合中有两个操作,一个是添加数据,另一个询问当前的前 K 大数据。
如果每次询问前 K 大数据,我们都基于当前的数据重新计算的话,那时间复杂度就是 O(nlogK),n 表示当前的数据的大小。
实际上,我们可以一直都维护一个 K 大小的小顶堆,当有数据被添加到集合中时,我们就拿它与堆顶的元素对比。
如果比堆顶元素大,我们就把堆顶元素删除,并且将这个元素插入到堆中;
如果比堆顶元素小,则不做处理。
这样,无论任何时候需要查询当前的前 K 大数据,我们都可以立刻返回给他。
堆的应用三:利用堆求中位数
前面我们讲了如何求 Top K 的问题,现在我们来讲下,如何求动态数据集合中的中位数。
中位数,顾名思义,就是处在中间位置的那个数。
如果数据的个数是奇数,把数据从小到大排列,那第 n/2+1 个数据就是中位数;
如果数据的个数是偶数的话,那处于中间位置的数据有两个,第 n/2 个和第 n/2+1 个数据,这个时候,我们可以随意取一个作为中位数,比如取两个数中靠前的那个,就是第 n/2个数据。
对于一组静态数据,中位数是固定的,我们可以先排序,第 n/2个数据就是中位数。
每次询问中位数的时候,我们直接返回这个固定的值就好了。
所以,尽管排序的代价比较大,但是边际成本会很小。
但是,如果我们面对的是动态数据集合,中位数在不停地变动,如果再用先排序的方法,
每次询问中位数的时候,都要先进行排序,那效率就不高了。
借助堆这种数据结构,我们不用排序,就可以非常高效地实现求中位数操作。我们来看看,它是如何做到的?
我们需要维护两个堆,一个大顶堆,一个小顶堆。
大顶堆中存储前半部分数据,小顶堆中存储后半部分数据,且小顶堆中的数据都大于大顶堆中的数据。
也就是说,如果有 n 个数据,n 是偶数,我们从小到大排序,那前 n/2 个数据存储在大顶堆中,后 n/2 个数据存储在小顶堆中。这样,大顶堆中的堆顶元素就是我们要找的中位数。如果 n 是奇数,情况是类似的,大顶堆就存储 n/2+1个数据,小顶堆中就存储 n/2 个数据。
我们前面也提到,数据是动态变化的,当新添加一个数据的时候,我们如何调整两个堆,让大顶堆中的堆顶元素继续是中位数呢?
如果新加入的数据小于等于大顶堆的堆顶元素,我们就将这个新数据插入到大顶堆;
否则,我们就将这个新数据插入到小顶堆。
这个时候就有可能出现,两个堆中的数据个数不符合前面约定的情况:
如果 n 是偶数,两个堆中的数据个数都是 n/2;
如果 n 是奇数,大顶堆有 n/2+1 个数据,小顶堆有 n2n2 个数据。
这个时候,我们可以从一个堆中不停地将堆顶元素移动到另一个堆,
通过这样的调整,来让两个堆中的数据满足上面的约定。
于是,我们就可以利用两个堆,一个大顶堆、一个小顶堆,实现在动态数据集合中求中位数的操作。
插入数据因为需要涉及堆化,所以时间复杂度变成了 O(logn),
但是求中位数我们只需要返回大顶堆的堆顶元素就可以了,所以时间复杂度就是 O(1)。
实际上,利用两个堆不仅可以快速求出中位数,还可以快速求其他百分位的数据,原理是类似的。
还记得我们在“为什么要学习数据结构与算法”里的这个问题吗?“如何快速求接口的 99% 响应时间?”
我们现在就来看下,利用两个堆如何来实现。
在开始这个问题的讲解之前,我先解释一下,什么是“99% 响应时间”。
中位数的概念就是将数据从小到大排列,处于中间位置,就叫中位数,这个数据会大于等于前面 50% 的数据。
99 百分位数的概念可以类比中位数,如果将一组数据从小到大排列,这个 99 百分位数就是大于前面 99% 数据的那个数据。
如果你还是不太理解,我再举个例子。
假设有 100 个数据,分别是 1,2,3,……,100,那 99 百分位数就是 99,因为小于等于 99 的数占总个数的 99%。
弄懂了这个概念,我们再来看 99% 响应时间。如果有 100 个接口访问请求,每个接口请求的响应时间都不同,比如 55 毫秒、100 毫秒、23 毫秒等,我们把这 100 个接口的响应时间按照从小到大排列,排在第 99 的那个数据就是 99% 响应时间,也叫 99 百分位响应时间。
我们总结一下,如果有 n 个数据,将数据从小到大排列之后,99 百分位数大约就是第 n*99% 个数据,同类,80 百分位数大约就是第 n*80% 个数据。
弄懂了这些,我们再来看如何求 99% 响应时间。
我们维护两个堆,一个大顶堆,一个小顶堆。假设当前总数据的个数是 n,大顶堆中保存 n*99% 个数据,小顶堆中保存 n*1% 个数据。大顶堆堆顶的数据就是我们要找的 99% 响应时间。
每次插入一个数据的时候,我们要判断这个数据跟大顶堆和小顶堆堆顶数据的大小关系,然后决定插入到哪个堆中。如果这个新插入的数据比大顶堆的堆顶数据小,那就插入大顶堆;如果这个新插入的数据比小顶堆的堆顶数据大,那就插入小顶堆。
但是,为了保持大顶堆中的数据占 99%,小顶堆中的数据占 1%,在每次新插入数据之后,我们都要重新计算,这个时候大顶堆和小顶堆中的数据个数,是否还符合 99:1 这个比例。如果不符合,我们就将一个堆中的数据移动到另一个堆,直到满足这个比例。移动的方法类似前面求中位数的方法,这里我就不啰嗦了。
通过这样的方法,每次插入数据,可能会涉及几个数据的堆化操作,所以时间复杂度是 O(logn)。每次求 99% 响应时间的时候,直接返回大顶堆中的堆顶数据即可,时间复杂度是 O(1)。
内容小结
堆是一种完全二叉树。
它最大的特性是:每个节点的值都大于等于(或小于等于)其子树节点的值。因此,堆被分成了两类,大顶堆和小顶堆。
堆中比较重要的两个操作是插入一个数据和删除堆顶元素。
这两个操作都要用到堆化。
插入一个数据的时候,我们把新插入的数据放到数组的最后,然后从下往上堆化;
删除堆顶数据的时候,我们把数组中的最后一个元素放到堆顶,然后从上往下堆化。
这两个操作时间复杂度都是 O(logn)。
除此之外,我们还讲了堆的一个经典应用,堆排序。
堆排序包含两个过程,建堆和排序。
我们将下标从 n/2 到 1 的节点,依次进行从上到下的堆化操作,然后就可以将数组中的数据组织成堆这种数据结构。
接下来,我们迭代地将堆顶的元素放到堆的末尾,并将堆的大小减一,然后再堆化,
重复这个过程,直到堆中只剩下一个元素,整个数组中的数据就都有序排列了。
优先级队列是一种特殊的队列,优先级高的数据先出队,而不再像普通的队列那样,先进先出。
实际上,堆就可以看作优先级队列,只是称谓不一样罢了。
求 Top K 问题又可以分为针对静态数据和针对动态数据,只需要利用一个堆,就可以做到非常高效率的查询 Top K 的数据。
求中位数实际上还有很多变形,比如求 99 百分位数据、90 百分位数据等,处理的思路都是一样的,
即利用两个堆,一个大顶堆,一个小顶堆,随着数据的动态添加,
动态调整两个堆中的数据,最后大顶堆的堆顶元素就是要求的数据。
来源:
数据结构与算法之美 王争