算法笔记——图论

最短路

• Floyed
  求任意两点间的最短路，最简单的三段循环，复杂度为$O(n^3)$。注意先枚举中间节点。
  代码：

for(int k=1;k<=n;++k)
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j)
dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);

• Dijkstra
  求单源最短路径，复杂度为$O(n^2)$或$O(n\log n)$。思想是蓝白点+队列，不能判负环，可以堆优化。
  代码：

#include
#include
#include
#define maxn 200005
#define maxm 800005
using namespace std;

priority_queue< pair<int,int> >qu;//堆优化dijkstra
struct node
{
	int v,val,next;
}tr[maxm],ne[maxm];
int n,m,s,e;
int tot,head[maxn];
int que[maxm];
int dis[maxn],vis[maxn];

void add(int x,int y,int z)
{
	tot++;
	tr[tot].v=y;
	tr[tot].val=z;
	tr[tot].next=head[x];
	head[x]=tot;
}

void dj()
{
	memset(dis,0x3f3f3f,sizeof(dis));
	dis[s]=0;
	qu.push(make_pair(0,s));
	while(qu.size())
	{
		int x=qu.top().second;//取出堆顶
		qu.pop();
		if(vis[x])continue;
		vis[x]=1;
		for(int t=head[x];t;t=tr[t].next)
		{
			int y=tr[t].v,z=tr[t].val;
			if(dis[y]>dis[x]+z)
			{
				dis[y]=dis[x]+z;
				qu.push(make_pair(-dis[y],y));
			}//把二元组插入堆
		}
	}
}//堆优化的dijkstra

int main()
{
	freopen("data.in","r",stdin);
	freopen("data.out","w",stdout);
	scanf("%d%d%d",&n,&m,&s);
	for(int i=1;i<=m;++i)
	{
		int x,y,z;
		scanf("%d%d%d",&x,&y,&z);
		add(x,y,z);
	}
	dj();//dijkstra求最短路
	for(int i=1;i<=n;++i)
	printf("%d ",dis[i]);
	return 0;
}

• Spfa
  求单源最短路径，可以判负环，最坏复杂度$O(mn)$，但容易被菊花图卡掉。
  代码：

#include
#include
#define ll long long
#define maxn 10005
#define maxm 500005
using namespace std;

struct node
{
    ll v,val,next;
}tr[maxm];
ll n,m,s;
ll tot,head[maxn];
ll dis[maxn],vis[maxn],q[maxm];

void add(ll x,ll y,ll z)
{
    tot++;
    tr[tot].v=y;
    tr[tot].next=head[x];
    tr[tot].val=z;
    head[x]=tot;
}

void spfa()
{
    ll top=0,hd=0;
    memset(dis,0x3f3f3f3f,sizeof(dis));
    vis[s]=1;
    dis[s]=0;
    q[++top]=s;
    while(hd<top)
    {
        int x=q[++hd];
        vis[x]=0;
        for(ll t=head[x];t;t=tr[t].next)
        {
            ll y=tr[t].v,z=tr[t].val;
            if(dis[y]>dis[x]+z)
            {
                dis[y]=dis[x]+z;
                if(!vis[y])
                {
                    q[++top]=y;
                    vis[y]=1;
                }
            }
        }
    }
}

int main()
{
    scanf("%lld%lld%lld",&n,&m,&s);
    for(ll i=1;i<=m;++i)
    {
        ll x,y,z;
        scanf("%lld%lld%lld",&x,&y,&z);
        add(x,y,z);
    }
    spfa();
    for(ll i=1;i<=n;++i)
    {
    	if(dis[i]>=0x3f3f3f3f3f)
    	printf("2147483647 ");
    	else printf("%lld ",dis[i]);
	}
    return 0;
}

• 总结
  如果有可能出现负环，直接用Spfa，否则首选Dijkstra堆优化。

• 应用
  1.求最短路；
  2.作为一些算法的辅助算法（如差分约束里需要用到Spfa判解）。

• 例题
  1.【模板】单源最短路径（弱化版）；
  2.【模板】单源最短路径（标准版）；
  3.【模板】负环（为什么用队列就那么快？？？）；

---

分层图

• 概念
  顾名思义，就是一张分成几个层次的图。
  这种题一般的套路是，给出一张图，求出最短路，但是这张图中可以选取$k$或者打一定的折扣。这种情况下就需要用到分层图。

• 方法
  这里介绍两种方法：
  1.与求普通的最短路大同小异，只是单源最短路的$dis[i]$数组要变成$dis[i][j]$，表示起点到节点$i$当中花费$j$条免费边的最短路径。状态转移很简单。
  2.拆点法。将每个点拆成k层点，相同层的边权为$val$，不同层的边权为0，最短路算法不变。

• 代码

1.dp法

#include
#include
#include
#define maxn 10005
#define maxm 50005
#define maxk 15
using namespace std;

struct node
{
	int v,val,next;
}tr[maxm<<1];
int n,m,k,s,t;
int tot,head[maxn];
int dis[maxn][maxk];
priority_queue<pair<int,int> >que;

void add(int x,int y,int z)
{
	tot++;
	tr[tot].v=y;
	tr[tot].val=z;
	tr[tot].next=head[x];
	head[x]=tot;
}

void dijstra()
{
	memset(dis,0x3f3f3f3f,sizeof(dis));
	for(int i=0;i<=k;++i)
	dis[s][i]=0;//初始化
	for(int i=0;i<=k;++i)//枚举次数
	{
		que.push(make_pair(0,s));
		while(que.size())
		{
			int x=que.top().second;
			que.pop();
			for(int t=head[x];t;t=tr[t].next)
			{
				int y=tr[t].v,z=tr[t].val,fl=0;
				if(i)
				{
					if(dis[y][i]>dis[x][i-1])//使用免费次数
					{
						dis[y][i]=dis[x][i-1];
						fl=1;
					}
				}
				if(dis[y][i]>dis[x][i]+z)//不使用次数
				{
					dis[y][i]=dis[x][i]+z;
					fl=1;
				}
				if(fl)
				que.push(make_pair(-dis[y][i],y));
			}
		}//分层图dp
	}
}//堆优化dijstra

int main()
{
	scanf("%d%d%d%d%d",&n,&m,&k,&s,&t);
	s++;t++;
	for(int i=1;i<=m;++i)
	{
		int x,y,z;
		scanf("%d%d%d",&x,&y,&z);
		x++;y++;
		add(x,y,z);
		add(y,x,z);
	}
	dijstra();
	printf("%d",dis[t][k]);
	return 0;
}

2.拆点法

#include
#include
#include
#define maxn 1000005
#define maxm 20000005
#define maxk 25
using namespace std;

struct node
{
	int v,val,next;
}tr[maxm<<1];
int n,m,k,ans;
int tot,head[maxn];
int dis[maxn],vis[maxn];
priority_queue<pair<int,int> >que;

void add(int x,int y,int z)
{
	tot++;
	tr[tot].v=y;
	tr[tot].val=z;
	tr[tot].next=head[x];
	head[x]=tot;
}

void dijstra()
{
	memset(dis,0x3f3f3f3f,sizeof(dis));
	dis[1]=0;
	que.push(make_pair(0,1));
	while(que.size())
	{
		int x=que.top().second;
		que.pop();
		if(vis[x])continue;
		vis[x]=1;
		for(int t=head[x];t;t=tr[t].next)
		{
			int y=tr[t].v,z=tr[t].val;
			if(dis[y]>dis[x]+z)
			{
				dis[y]=dis[x]+z;
				que.push(make_pair(-dis[y],y));
			}
		}
	}
}//dijstra

int main()
{
	scanf("%d%d%d",&n,&m,&k);
	for(int i=1;i<=m;++i)
	{
		int x,y,z;
		scanf("%d%d%d",&x,&y,&z);
		add(x,y,z);
		add(y,x,z);
		for(int j=1;j<=k;++j)
		{
			add(j*n+x,j*n+y,z);
			add(j*n+y,j*n+x,z);//分层建图
			add((j-1)*n+x,j*n+y,0);
			add((j-1)*n+y,j*n+x,0);//每层建的权值为0
		}
	}
	dijstra();
	ans=dis[n];
	for(int i=1;i<=k;++i)
	ans=min(ans,dis[i*n+n]);
	printf("%d",ans);
	return 0;
}

个人还是喜欢dp法。
模板题：
1.[USACO09FEB]改造路Revamping Trails；
2.[JLOI2011]飞行路线；
3.[BJWC2012]冻结；

还有一种分层图可以用二分答案的方法解决，这里不细讲，给出一道例题：
电话线。

---

生成树

• 算法
  Prim算法。
• 思想
  贪心。
• 代码（此处是最小生成树）

#include
#include
using namespace std;
struct node
{
    int u,v,d;
}len[200005];
int m,n,fa[100005];

int find(int x)
{
    return fa[x]==x ? x : fa[x]=find(fa[x]); 
}//路径压缩

void unnion(int x,int y)
{
    x=find(x),y=find(y);
    fa[x]=y;
}

int judge(int x,int y)
{
    x=find(x),y=find(y);
    if(x==y)return 1;
    return 0;
}//手写并查集

bool cmp(node x,node y)
{
    return x.d<y.d;
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    fa[i]=i;
    for(int i=1;i<=m;i++)
    {
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        len[i].u=x,len[i].v=y,len[i].d=z;
    }
    sort(len+1,len+1+m,cmp);
    int sum=0,ans=0;
    for(int i=1;i<=m;i++)
    {
        if(judge(len[i].u,len[i].v))continue;
        unnion(len[i].u,len[i].v);
    	sum++;
    	ans+=len[i].d;
    	if(sum==n-1)
    	{
    		printf("%d",ans);
    		return 0;
    	}
    }
    if(sum==n)printf("%d",ans);
    else printf("orz");
    return 0;
}

• 习题
  1.货车运输（最大生成树）；

---

差分约束

• 作用
  解不等式组；
• 思想
  转化为图论，通过不等关系建图。
  如：$a_i-b_i\le c_i$可转化为在$a_i$和$b_i$间建立一条长为$c_i$的单项边。
• 代码

#include
#include
#include
#define maxn 20005
#define maxm 20005
using namespace std;

struct node
{
    int v,val,next;
}tr[maxm];
int m,n;
int tot,head[maxn];
int cnt[maxn],dis[maxn],vis[maxn];
queue<int>q;

void add(int x,int y,int z)
{
    tot++;
    tr[tot].v=y;
    tr[tot].val=z;
    tr[tot].next=head[x];
    head[x]=tot;
}//建边

int spfa()
{
    memset(dis,0x3f3f3f3f,sizeof(dis));
    for(int i=1;i<=n;++i)
    {
    	q.push(i);
    	vis[i]=1;
    }
    dis[1]=0;
    while(q.size())
    {
        int x=q.front();
        q.pop();
        vis[x]=0;
        for(int t=head[x];t;t=tr[t].next)
        {
            int y=tr[t].v,z=tr[t].val;
			cnt[y]=cnt[x]+1;
            if(cnt[y]>n)
            return 0;//判负环
            if(dis[y]>dis[x]+z)
            {
                dis[y]=dis[x]+z;
                if(!vis[y])
				{
					q.push(y);
					vis[y]=1; 
				}
            }//更新最短路
        }
    }
    return 1;
}

void work1()
{
    int a,b,c;
    scanf("%d%d%d",&a,&b,&c);
    if(a==b&&c!=0)
    {
    	printf("No");
    	return;
    }
    add(b,a,-c);
}//a-b>=c转化为b-a<=-c

void work2()
{
    int a,b,c;
    scanf("%d%d%d",&a,&b,&c);
    if(a==b&&c!=0)
    {
    	printf("No");
    	return;
    }
    add(a,b,c);
}//a-b<=c

void work3()
{
    int a,b;
    scanf("%d%d",&a,&b);
    add(a,b,0);
    add(b,a,0);
}//a-b==0转化为a-b<=0&&b-a<=0 

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;++i)
    {
        int flag;
        scanf("%d",&flag);
        if(flag==1)
        work1();
        else if(flag==2)
        work2();
        else if(flag==3)
        work3();
    }
    if(!spfa())
    printf("No");
    else printf("Yes");
    return 0;
}

模板题：小K的农场;

---

拓扑排序

• 概念
  对于一个有向图，若做事有先后顺序，可以用拓扑排序。

• 思想
  队列或栈（大多数情况下用的是队列）。
  先扫描一遍，若点$i$的度数为1，入队。
  结下来，对于队列中每个元素，枚举与它相连的节点$x$，使$x$度数减1，若$x$的度数为1，$x$入读，以此类推。

• 代码

#include
using namespace std;
int indgr[105],stackk[105],s[105][105],n,top=0;
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		int x;
		scanf("%d",&x);
		while(x!=0)
		{
			indgr[x]++;
			s[i][x]=1;
			scanf("%d",&x);
		}
	}//输入，记录入度
	for(int i=1;i<=n;i++)
	if(indgr[i]==0)
	{
		top++;
		stackk[top]=i;//初始化，将入度为0的点入栈
	}
	while(top>0)
	{
		int v=stackk[top];
		printf("%d ",v);
		top--;//顶点出栈 
		for(int j=1;j<=n;j++)
		if(s[v][j]==1)
		{
			indgr[j]--;//删除与当前顶点相连的边
			if(indgr[j]==0)stackk[++top]=j;//入栈
		}
	}
	return 0;
}

---

Tarjan算法及其应用

• tarjan缩点
  针对有向图或无向图的强连通分量，将有向图或无向图中的强联通分量缩成一个点，这样就不会因为在环中跑而TLE了，搭配拓扑排序食用绝佳。

下面给出tarjan缩点加上拓扑排序的实例。
代码：

#include
#define maxn 10005
#define maxm 50005
using namespace std;

struct node
{
    int v,next;
}tr[maxm];
int n,m;
int head[maxn],tot;
int out[maxn];
int stk[maxn],co[maxn],low[maxn],dfn[maxn],sum[maxn],top,col,num;
int flag,ans;

int min(int a,int b)
{
    return a<b?a:b;
}

void add(int x,int y)
{
    tot++;
    tr[tot].v=y;
    tr[tot].next=head[x];
    head[x]=tot;
}

void tarjan(int u)
{
    stk[++top]=u;
    low[u]=dfn[u]=++num;
    for(int t=head[u];t;t=tr[t].next)
    {
        int v=tr[t].v;
        if(!dfn[v])
        {
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }//更新树边
        else if(!co[v])
        {
            low[u]=min(low[u],dfn[v]);
        }
    }
    if(low[u]==dfn[u])
    {
        co[u]=++col;
        sum[col]++;
        while(stk[top]!=u)
        {
            co[stk[top--]]=col;
            sum[col]++;//统计联通块中的元素个数
        }
        top--;
    }
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;++i)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        add(x,y);
    }
    for(int i=1;i<=n;++i)
    {
        if(!dfn[i])
        tarjan(i);
    }
    for(int i=1;i<=n;++i)
    {
        for(int t=head[i];t;t=tr[t].next)
        {
            int v=tr[t].v;
            if(co[i]!=co[v])
            out[co[i]]++;//统计出度
        }
    }//建新图
    for(int i=1;i<=col;++i)
    {
        if(out[i]==0)
        {
            if(flag==1)
            {
                printf("0");
                return 0;
            }
            else
            {
                flag=1;
                ans=sum[i];
            }
        }
    }
    printf("%d",ans);
    return 0;
}

模板题：【模板】缩点；

• tarjan割点（V-DCC）

所谓割点，即图中的一个点，去掉这个点和这个点所连的边后，能将图分成两个部分。
找割点的代码：

#include
#define maxn 5005
using namespace std;

struct node
{
	int v,next;
}tr[maxn<<1];
int n,m;
int tot,head[maxn];
int timer,ans,root,dfn[maxn],low[maxn],cut[maxn];//dfn[x]是x的dfs序,low[x]是x可以扫到的dfs序最小的节点

int min(int x,int y)
{
	return x<y?x:y;
}

void add(int x,int y)
{
	tot++;
	tr[tot].v=y;
	tr[tot].next=head[x];
	head[x]=tot;
}//建图

void tarjan(int u)
{
	dfn[u]=low[u]=++timer;//初始化更新时间戳
	int tot=0;
	for(int t=head[u];t;t=tr[t].next)
	{
		int y=tr[t].v;
		if(!dfn[y])
		{
			tarjan(y);
			low[u]=min(low[u],low[y]);//更新low[u]
			if(low[y]>=dfn[u])
			{
				tot++;
				if(u!=root||tot>=2)
				cut[u]=1;//找到割点
			}//x可以把图分成两个不连通的部分
		}//若y未被扫描过则去扫描y
		else low[u]=min(low[u],dfn[y]);//更新low[x]
	}
}

int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;++i)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		add(x,y);
		add(y,x);
	}
	for(int i=1;i<=n;++i)
	{
		if(!dfn[i])
		{
			root=i;
			tarjan(i);
		}
	}//扫描割点
	for(int i=1;i<=n;++i)
	{
		if(cut[i])
		ans++;
	}
	printf("%d",ans);
	return 0;
}

• tarjan割边

割边，就是桥，即若去掉桥，则该图不连通。
代码：

#include
#define maxn 50005
using namespace std;

struct node
{
    int v,next;
}tr[maxn<<1];
int n,m;
int tot,head[maxn];
int timer,ans,bridge[maxn<<1],dfn[maxn],low[maxn];

int min(int x,int y)
{
    return x<y?x:y;
}

void add(int x,int y)
{
    tot++;
    tr[tot].v=y;
    tr[tot].next=head[x];
    head[x]=tot;
}//建图

void tarjan(int u,int in_edge)
{
    dfn[u]=low[u]=++timer;
    for(int t=head[u];t;t=tr[t].next)
    {
        int y=tr[t].v;
        if(!dfn[y])
        {
            tarjan(y,t);
            low[u]=min(low[u],low[y]);
            if(low[y]>dfn[u])
            bridge[t]=bridge[t^1]=1;//标记割边(需标记双向边)
        }
        else if(t!=(in_edge^1))
        low[u]=min(low[u],dfn[y]);//我也看不懂QAQ
    }
}

int main()
{
    scanf("%d%d",&n,&m);
    tot=1;
    for(int i=1;i<=m;++i)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        add(x,y);
        add(y,x);
    }
    for(int i=1;i<=n;++i)
    {
        if(!dfn[i])
        tarjan(i,0);
    }
    for(int i=2;i<tot;i+=2)
    {
        if(bridge[i])
        ans++;
    }
    printf("%d",ans);
    return 0;
}

因为以上内容均为省选内容，所以我说的比较简略（其实是我看不懂）。

---

2-sat

安利博客：2-sat思想及入门；
所以，，，上代码：

#include
#define maxn 2000005
using namespace std;

struct node
{
	int v,next;
}tr[maxn<<1];
int n,m;
int tot,head[maxn];
int timer,col,top,stk[maxn],dfn[maxn],low[maxn],co[maxn],vis[maxn];//tarjan判是否成立,求拓扑序列
int ans[maxn];

int min(int x,int y)
{
	return x<y?x:y;
}

void add(int x,int y)
{
	tot++;
	tr[tot].v=y;
	tr[tot].next=head[x];
	head[x]=tot;
}

void tarjan(int x)
{
	stk[++top]=x;
	dfn[x]=low[x]=++timer;
	for(int t=head[x];t;t=tr[t].next)
	{
		int y=tr[t].v;
		if(!dfn[y])
		{
			tarjan(y);
			low[x]=min(low[x],low[y]);
		}
		else if(!co[y])
		low[x]=min(low[x],dfn[y]);
	}
	if(dfn[x]==low[x])
	{
		co[x]=++col;
		while(stk[top]!=x)
		{
			co[stk[top]]=col;
			top--;
		}
		top--;
	}//成环
}//tajan求强连通分量和反着的拓扑序

int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;++i)
	{
		int x,xx,y,yy;
		scanf("%d%d%d%d",&x,&xx,&y,&yy);
		add(x+n*(xx&1),y+n*(yy^1));
		add(y+n*(yy&1),x+n*(xx^1));//位运算优化
	}//x为真,x+n为假
	for(int i=1;i<=2*n;++i)
	{
		if(!dfn[i])
		tarjan(i);
	}
	for(int i=1;i<=n;++i)
	{
		if(co[i]==co[i+n])
		{
			printf("IMPOSSIBLE");
			return 0;
		}
	}//i和i+n在同一个强连通分量里
	printf("POSSIBLE\n");
	for(int i=1;i<=n;++i)
	printf("%d ",co[i]<co[i+n]);
	return 0;
}
/*
if (va && vb)
{ // a, b 都真，-a -> b, -b -> a
    g[a + n].push_back(b);
    g[b + n].push_back(a);
}
else if (!va && vb)
{ // a 假 b 真，a -> b, -b -> -a
    g[a].push_back(b);
    g[b + n].push_back(a + n);
}
else if (va && !vb)
{ // a 真 b 假，-a -> -b, b -> a
    g[a + n].push_back(b + n);
    g[b].push_back(a);
}
else if (!va && !vb)
{ // a, b 都假，a -> -b, b -> -a
    g[a].push_back(b + n);
    g[b].push_back(a + n);
}
*/

习题：
1.【模板】2-SAT 问题；
2.[JSOI2010]满汉全席；

---

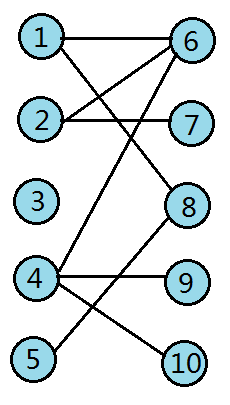
二分图

• 概念
  把一张图分成两个区间，同一个区间内不能连边，这样的图就是二分图。
  像这样：
  

• 二分图的匹配
  左边一个连右边一个，且每个节点只能被匹配一次，这就是二分图的匹配。

• 匈牙利算法
  1.作用
  求二分图最大匹配。
  2.流程
  不断寻找增广路，直到找不到为止，就求出了二分图的最大匹配。（注意，建图时最好建立单向边）

• 代码

#include
#include
using namespace std;
#define maxn 405
#define maxm 60005
struct node
{
	int v,next;
}tr[maxm];
int match[maxn],head[maxn],vis[maxn];
int n,p,cnt,tot,timer;
void add(int x,int y)
{
	tot++;
	tr[tot].v=y;
	tr[tot].next=head[x];
	head[x]=tot;
}

int dfs(int x)//找增广路
{
	for(int t=head[x];t;t=tr[t].next)
	{
		int y=tr[t].v;
		if(vis[y]==timer) continue;
		vis[y]=timer;
		if(!match[y]||dfs(match[y]))
		{
			match[y]=x;
			return 1;
		}
	}
	return 0;
}

int main()
{
	int T;
	scanf("%d",&T);
	while(T--)
	{
		tot=0;
		scanf("%d%d",&p,&n);
		for(int i=1;i<=p;i++)
		{
			scanf("%d",&cnt);
			while(cnt--)
			{
				int x;
				scanf("%d",&x);
				add(i,p+x);
			}//建立二分图
		}
		int ans=0;
		for(int i=1;i<=p;i++)
		{
			timer++;
			if(dfs(i))ans++;
		}
		if(ans==p)
		printf("YES\n");
		else printf("NO\n");
		for(int i=1;i<=p+n;++i)head[i]=0;
		for(int i=1;i<=p+n;++i)match[i]=0;
	}
	return 0;
}

• 习题
  1.【模板】二分图匹配；
  2.[NOI2009]变换序列；
  3.[HEOI2016/TJOI2016]游戏；

---

网络流

因为种类太多，所以直接给模板了。

• 最大流（最小割）

#include
#include
#define maxn 10005
#define maxm 200005
using namespace std;

struct node
{
    int v,val,next;
}tr[maxm];
int n,m,s,e;
int tot=1,head[maxn];//从2开始存，保证异或
int timer,dis[maxn],qu[maxm],vis[maxn];

int min(int a,int b)
{
    return a<b?a:b; 
}

void add(int x,int y,int z)
{
    tot++;
    tr[tot].v=y;
    tr[tot].val=z;
    tr[tot].next=head[x];
    head[x]=tot;
} 

void Add(int x,int y,int z)
{
    add(x,y,z);
    add(y,x,0);
}

int bfs()
{
    int hd=0,top=0;
    qu[++top]=s;
    dis[s]=0;
    vis[s]=++timer;//起点入队,timer判断入队时间
    while(hd<top)
    {
        int x=qu[++hd];
        for(int t=head[x];t!=-1;t=tr[t].next)
        {
            int y=tr[t].v,z=tr[t].val;
            if(z==0)continue;
            if(vis[y]!=timer)
            {
                vis[y]=timer;
                dis[y]=dis[x]+1;
                qu[++top]=y;
            }//拓展节点,寻找增广路
        }
    }
    return vis[e]==timer;//找到增广路返回1,反之返回2
}

int dfs(int x,int lim)
{
    if(x==e)return lim;//到达终点
    int ans=0;
    for(int t=head[x];t!=-1;t=tr[t].next)
    {
        int y=tr[t].v,z=tr[t].val;
        if(z!=0&&dis[y]==dis[x]+1)//有流量且相连
        {
            int nw=dfs(y,min(z,lim));
            if(nw!=0)
            {
                tr[t].val-=nw;
            	tr[t^1].val+=nw;
            	lim-=nw;
            	ans+=nw;
            	if(lim==0)
            	return ans;
            }	
        }
    }
    return ans;
}

int dinic()
{
    int ans=0;
    while(bfs())ans+=dfs(s,0x3f3f3f3f);
    return ans;
}

int main()
{
    memset(head,-1,sizeof(head));
    scanf("%d%d%d%d",&n,&m,&s,&e);
    for(int i=1;i<=m;i++)
    {
    	int x,y,z;
    	scanf("%d%d%d",&x,&y,&z);
    	Add(x,y,z);
	}
    printf("%d",dinic());
    return 0;
}

模板：
1.【模板】网络最大流；
2.酒店之王；

• 费用流
  最小费用最大流：

#include
#include
#include
#define inf 0x3f3f3f3f
#define maxn 50005
#define maxm 150005
using namespace std;

struct node
{
	int u,v,next,val,cost;
}tr[maxm];
int tot=1,head[maxn];
int hd,tp,que[maxm<<2],dis[maxn],in[maxn],pre[maxn];//建队
int n,m,s,t;
int ans,ans2;

void add(int x,int y,int w,int va)
{
	tot++;
	tr[tot].u=x;
	tr[tot].v=y;
	tr[tot].next=head[x];
	tr[tot].val=w;
	tr[tot].cost=va;
	head[x]=tot;
}//建边

void Add(int x,int y,int w,int va)
{
	add(x,y,w,va);
	add(y,x,0,-va);//建立反向边,注意单位费用为-va
}

void spfa()
{
	memset(dis,inf,sizeof(dis));
	memset(que,0,sizeof(que));
	memset(in,0,sizeof(in));
	hd=tp=0;
	dis[s]=0;
	que[++tp]=s;
	in[s]=1;//初始化队列
	while(hd<tp)
	{
		int x=que[++hd];
		in[x]=0;
		for(int i=head[x];i!=-1;i=tr[i].next)
		{
			int y=tr[i].v;
			if(tr[i].val&&dis[y]>dis[x]+tr[i].cost)
			{
				pre[y]=i;//记录y连接的边
				dis[y]=dis[x]+tr[i].cost;
				if(!in[y])
				{
					que[++tp]=y;
					in[y]=1;
				}//将y入队,标记节点
			}//更新费用的最短路
		}
	}
}//spfa求增广路

void price()
{
	while(spfa(),dis[t]<inf)
	{
		int nw=inf;
		for(int i=pre[t];i;i=pre[tr[i].u])
		nw=min(nw,tr[i].val);//求出最小剩余流量
		ans+=dis[t]*nw;
		ans2+=nw;
		for(int i=pre[t];i;i=pre[tr[i].u])
		{
			tr[i].val-=nw;
			tr[i^1].val+=nw;
		}
	}
}//求出最小费用

int main()
{
	memset(head,-1,sizeof(head));
	scanf("%d%d%d%d",&n,&m,&s,&t);
	for(int i=1;i<=m;++i)
	{
		int x,y,w,va;
		scanf("%d%d%d%d",&x,&y,&w,&va);
		Add(x,y,w,va);
	}
	price();//求费用流
	printf("%d %d",ans2,ans);
	return 0;
}

模板：【模板】最小费用最大流；

• 无源汇可行流

• 有源汇可行流

---

线段树优化建图

因为是写了博客的，所以不细讲，直接见博客吧！
线段树优化建图

• 代码

#include
#include
#define maxn 4000005
#define lid ls[k]
#define rid rs[k]
using namespace std;

struct node
{
	int v,next;
}tr[maxn*10];
int n,m,rt,ndnum,ans;
int id[maxn],dp[maxn],nw[maxn],in[maxn];
int ls[maxn*4],rs[maxn*4],fl[maxn*4];//线段树
int tot,head[maxn];
int hd,top,que[maxn];

void add(int x,int y)
{
	tot++;
	tr[tot].v=y;
	tr[tot].next=head[x];
	head[x]=tot;
	in[y]++;//统计入度
}

void build(int &k,int l,int r)
{
	if(l==r)
	{
		k=l;
		return;
	}
	k=++ndnum;//传新编号
	int mid=(l+r)>>1;
	build(lid,l,mid);
	build(rid,mid+1,r);//下传左右儿子
	add(lid,k);
	add(rid,k);//向父节点连边
}

void addtr(int k,int L,int R,int l,int r)
{
	if(L>=l&&R<=r)
	{
		add(k,ndnum);//等级小连等级大
		return;
	}
	int mid=(L+R)>>1;
	if(l<=mid)
	addtr(lid,L,mid,l,r);
	if(r>mid)
	addtr(rid,mid+1,R,l,r);
}//线段树优化建边

void topusort()
{
	for(int i=1;i<=ndnum;++i)
	{
		if(!in[i])
		{
			que[++top]=i;
			if(i<=n)dp[i]=1;//赋初值
		}
	}
	while(hd<top)
	{
		int x=que[++hd];
		ans=max(ans,dp[x]);
		for(int t=head[x];t;t=tr[t].next)
		{
			int y=tr[t].v;
			dp[y]=max(dp[y],dp[x]+(y<=n));//状态转移
			in[y]--;
			if(!in[y])
			que[++top]=y;
		}
	}
}

int main()
{
	freopen("c.in","r",stdin);
	freopen("c.out","w",stdout);
	scanf("%d%d",&n,&m);
	ndnum=n;//从n开始建边
	build(rt,1,n);
	for(int i=1;i<=m;++i)
	{
		int x;
		scanf("%d",&x);
		ndnum++;//建虚点
		for(int j=1;j<=x;++j)
		{
			scanf("%d",&nw[j]);
			add(ndnum,nw[j]);
		}
		for(int j=1;j<x;++j)
		{
			if(nw[j]+1!=nw[j+1])
			addtr(n+1,1,n,nw[j]+1,nw[j+1]-1);//线段树优化建边(等级小连等级大)
		}
	}
	topusort();
	printf("%d",ans);
	return 0;
}

对应例题：
车站分级