Verilog设计实例(4)详解全类别加法器(一)
博文目录
-
- 写在前面
- 正文
-
- 半加器
-
- 设计代码
- 测试文件
- 行为仿真波形图
- 全加器
-
- 设计文件
- 设计完整文件
- 行为仿真
- 纹波进位加法器
-
- 2bit数据等波纹加法设计
- 参数化的等波纹加法器设计
- 参考资料
- 交个朋友
写在前面
博客首页
本文详细地总结了一系列的加法器,包括半加器、全加器、等波纹进位加法器,虽然FPGA设计工程师不会设计这些东西作为模块来使用,因为综合工具足够智能,能够识别数据相加,但作为训练材料不失为一种不错的选择。
正文
❖ ❖ ❖
半加器
半加器是新数字设计师的基本构建块。 半加器显示了如何用几个逻辑门将两个位相加。 实际上,它们不常用,因为它们仅限于两个1位输入。 为了将更大的数字加在一起,可以使用全加器。 一个半加法器具有两个一位输入,一个求和输出和一个进位输出。 请参考下面的真值表以了解这些位的工作方式。 接下来会给出创建半加器的Verilog描述以及仿真测试平台。
Half Adder Truth Table
| A | B | Carry | Sum |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
设计代码
module half_adder(
input i_bit1,
input i_bit2,
output o_carry,
output o_sum
);
assign o_carry = i_bit1 & i_bit2; //bitwise and
assign o_sum = i_bit1 ^ i_bit2; //bitwise xor
endmodule
测试文件
module half_adder_tb;
reg i_bit1;
reg i_bit2;
wire o_carry;
wire o_sum;
initial begin
i_bit1 = 0;
i_bit2 = 0;
# 10
i_bit1 = 0;
i_bit2 = 1;
# 10
i_bit1 = 1;
i_bit2 = 0;
# 10
i_bit1 = 1;
i_bit2 = 1;
#10 $finish;
end
// Monitor values of these variables and print them into the log file for debug
initial
$monitor ("i_bit1 = %0b, i_bit2 = %0b, o_sum = %0b, o_carry = %0b", i_bit1, i_bit2, o_sum, o_carry);
half_adder inst_half_adder(
.i_bit1(i_bit1),
.i_bit2(i_bit2),
.o_sum(o_sum),
.o_carry(o_carry)
);
endmodule
行为仿真波形图
i_bit1 = 0, i_bit2 = 0, o_sum = 0, o_carry = 0
i_bit1 = 0, i_bit2 = 1, o_sum = 1, o_carry = 0
i_bit1 = 1, i_bit2 = 0, o_sum = 1, o_carry = 0
i_bit1 = 1, i_bit2 = 1, o_sum = 0, o_carry = 1
❖ ❖ ❖
全加器
全加器也是新数字设计师的基本构建块。 许多数字设计入门课程向初学者全面介绍。 一旦了解了全加法器的工作原理,就可以看到仅使用简单的门就可以构建更复杂的电路。不过要说清楚的是,实际上,FPGA设计人员并不是手工编写完整的加法器。 工具已足够先进到可以知道如何将两个数字相加。 但这仍然是一个很好的练习,这就是为什么要在这里进行介绍。
单个全加器具有两个一位输入,一个进位输入,一个求和输出和一个进位输出。 它们中的许多可以一起使用以创建纹波进位加法器,该纹波进位加法器可以用于将大数相加。 单个全加器如下图所示。

全加器的真值表如下:
Full Adder Truth Table
| A | B | Cin | Cout | Sum |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
由真值表可以得出全加器的进位输出以及和的电路(表达式):
设计文件
可以直接看出实现上述加法器的方式有三种:
- 第一种:
//More clear method
wire w_WIRE_1;
wire w_WIRE_2;
wire w_WIRE_3;
assign w_WIRE_1 = i_bit1 ^ i_bit2;
assign w_WIRE_2 = w_WIRE_1 & i_carry;
assign w_WIRE_3 = i_bit1 & i_bit2;
assign o_sum = w_WIRE_1 ^ i_carry;
assign o_carry = w_WIRE_2 | w_WIRE_3;
- 第二种:
assign o_sum = i_bit1 ^ i_bit2 ^ i_carry;
assign o_carry = (i_bit1 ^ i_bit2) & i_carry) | (i_bit1 & i_bit2);
- 第三种
assign {o_carry, o_sum} = i_bit1 + i_bit2 + i_carry;
无疑,第一种和 第二种等价,那么第三种呢?是否和第一二种生成的结构等价呢?
这里以Vivado为例,看其如何综合:
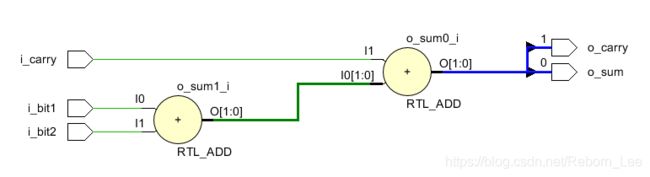
第一种、第二种:
RTL 原理图
综合之后原理图
第三种:
RTL 原理图
综合之后的原理图
对比第一种第二种就可以发现,综合后的原理图是一致的,这已经说明综合工具已足够强大,不需要我们从RTL级别描述,而直接描述其行为也可。
如果有不清楚Verilog的描述方式的区别,这里推荐看下Verilog的三种描述方式:
【 Verilog HDL 】HDL的三种描述方式
设计完整文件
`timescale 1ns / 1ps
///
// Engineer: Reborn Lee
// Module Name: full_adder
// https://blog.csdn.net/Reborn_Lee
module full_adder(
input i_bit1,
input i_bit2,
input i_carry,
output o_sum,
output o_carry
);
assign o_sum = i_bit1 ^ i_bit2 ^ i_carry;
assign o_carry = ((i_bit1 ^ i_bit2) & i_carry) | (i_bit1 & i_bit2);
// More clear method
// wire w_WIRE_1;
// wire w_WIRE_2;
// wire w_WIRE_3;
// assign w_WIRE_1 = i_bit1 ^ i_bit2;
// assign w_WIRE_2 = w_WIRE_1 & i_carry;
// assign w_WIRE_3 = i_bit1 & i_bit2;
// assign o_sum = w_WIRE_1 ^ i_carry;
// assign o_carry = w_WIRE_2 | w_WIRE_3;
// The third method
// assign {o_carry, o_sum} = i_bit1 + i_bit2 + i_carry;
endmodule
行为仿真
验证三种等价方式:
i_bit1 = 0, i_bit2 = 0, i_carry = 0, o_sum = 0, o_carry = 0
i_bit1 = 0, i_bit2 = 0, i_carry = 1, o_sum = 1, o_carry = 0
i_bit1 = 0, i_bit2 = 1, i_carry = 0, o_sum = 1, o_carry = 0
i_bit1 = 0, i_bit2 = 1, i_carry = 1, o_sum = 0, o_carry = 1
i_bit1 = 1, i_bit2 = 0, i_carry = 0, o_sum = 1, o_carry = 0
i_bit1 = 1, i_bit2 = 0, i_carry = 1, o_sum = 0, o_carry = 1
i_bit1 = 1, i_bit2 = 1, i_carry = 0, o_sum = 0, o_carry = 1
i_bit1 = 1, i_bit2 = 1, i_carry = 1, o_sum = 1, o_carry = 1
第三种仿真图:
i_bit1 = 0, i_bit2 = 0, i_carry = 0, o_sum = 0, o_carry = 0
i_bit1 = 0, i_bit2 = 0, i_carry = 1, o_sum = 1, o_carry = 0
i_bit1 = 0, i_bit2 = 1, i_carry = 0, o_sum = 1, o_carry = 0
i_bit1 = 0, i_bit2 = 1, i_carry = 1, o_sum = 0, o_carry = 1
i_bit1 = 1, i_bit2 = 0, i_carry = 0, o_sum = 1, o_carry = 0
i_bit1 = 1, i_bit2 = 0, i_carry = 1, o_sum = 0, o_carry = 1
i_bit1 = 1, i_bit2 = 1, i_carry = 0, o_sum = 0, o_carry = 1
i_bit1 = 1, i_bit2 = 1, i_carry = 1, o_sum = 1, o_carry = 1
必然也是没有任何问题的!
❖ ❖ ❖
纹波进位加法器
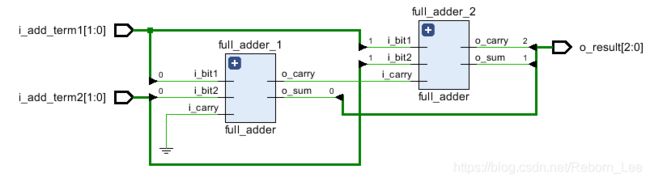
纹波进位加法器由许多级联在一起的全加法器组成。 它仅通过简单的逻辑门就可以将两个二进制数相加。 下图显示了连接在一起以产生4位纹波进位加法器的4个全加器。
同样需要指出的是,FPGA设计人员通常不需要手动实现纹波进位加法器。 FPGA工具足够聪明,足以知道如何将两个二进制数相加。 本练习的目的是说明基本电路如何工作以执行简单的任务。 对于初学者来说,这是一个很好的例子。
本文先实现一个2bits 的数据等波纹加法,之后采用generate for的方式实现任意位数数据的等波纹加法。
2bit数据等波纹加法设计
设计文件
`include "full_adder.v"
module ripple_carry_adder_2
(
input [1:0] i_add_term1,
input [1:0] i_add_term2,
output [2:0] o_result
);
wire [2:0] w_CARRY;
wire [1:0] w_SUM;
// No carry input on first full adder
assign w_CARRY[0] = 1'b0;
full_adder full_adder_1
(
.i_bit1(i_add_term1[0]),
.i_bit2(i_add_term2[0]),
.i_carry(w_CARRY[0]),
.o_sum(w_SUM[0]),
.o_carry(w_CARRY[1])
);
full_adder full_adder_2
(
.i_bit1(i_add_term1[1]),
.i_bit2(i_add_term2[1]),
.i_carry(w_CARRY[1]),
.o_sum(w_SUM[1]),
.o_carry(w_CARRY[2])
);
assign o_result = {w_CARRY[2], w_SUM}; // Verilog Concatenation
endmodule // ripple_carry_adder_2_FA
仿真文件
`timescale 1ns / 1ps
//
// Engineer: Reborn Lee
// Module Name: ripple_adder_2_tb
// Additional Comments:
// https://blog.csdn.net/Reborn_Lee
//
module ripple_adder_2_tb;
reg [1:0] i_add_term1;
reg [1:0] i_add_term2;
wire [2:0] o_result;
initial begin
i_add_term1 = 2'b00;
i_add_term2 = 2'b00;
# 10
i_add_term1 = 2'b10;
i_add_term2 = 2'b01;
# 10
i_add_term1 = 2'b11;
i_add_term2 = 2'b01;
# 10
i_add_term1 = 2'b11;
i_add_term2 = 2'b11;
#10 $finish;
end
// Monitor values of these variables and print them into the log file for debug
initial
$monitor ("i_add_term1 = %b, i_add_term2 = %b, o_result = %b", i_add_term1, i_add_term2, o_result);
ripple_carry_adder_2 inst_ripple_adder_2(
.i_add_term1(i_add_term1),
.i_add_term2(i_add_term2),
.o_result(o_result)
);
endmodule
仿真文件结构
仿真波形
i_add_term1 = 00, i_add_term2 = 00, o_result = 000
i_add_term1 = 10, i_add_term2 = 01, o_result = 011
i_add_term1 = 11, i_add_term2 = 01, o_result = 100
i_add_term1 = 11, i_add_term2 = 11, o_result = 110
参数化的等波纹加法器设计
上面的纹波进位加法器使用Verilog参数来允许同一代码的不同实现。 这使代码更具通用性和可重用性。 该代码使用该参数创建一个generate语句,该语句实例化WIDTH参数指定的数量的全加器。
这段代码显示了在创建紧凑但可扩展的代码时,强大的参数和generate语句的功能。 它可以用于任何宽度的输入。 数字设计师只需要为自己的特定应用适当设置宽度,工具就会生成正确的逻辑量!
设计文件
`timescale 1ns / 1ps
`include "full_adder.v"
module ripple_carry_adder
#(parameter WIDTH = 4)
(
input [WIDTH-1:0] i_add_term1,
input [WIDTH-1:0] i_add_term2,
output [WIDTH:0] o_result
);
wire [WIDTH:0] w_CARRY;
wire [WIDTH-1:0] w_SUM;
// No carry input on first full adder
assign w_CARRY[0] = 1'b0;
genvar ii;
generate
for (ii=0; ii设计文件结构
`timescale 1ns / 1ps
///
// Engineer: Reborn Lee
// Module Name: ripple_carry_adder_tb
// Additional Comments:
// https://blog.csdn.net/Reborn_Lee
///
module ripple_carry_adder_tb;
parameter WIDTH = 4;
reg [WIDTH-1:0] i_add_term1;
reg [WIDTH-1:0] i_add_term2;
wire [WIDTH:0] o_result;
initial begin
i_add_term1 = 'd5;
i_add_term2 = 'd11;
# 10
i_add_term1 = 'd6;
i_add_term2 = 'd15;
# 10
i_add_term1 = 'd11;
i_add_term2 = 'd13;
# 10
i_add_term1 = 'd15;
i_add_term2 = 'd15;
#10 $finish;
end
// Monitor values of these variables and print them into the log file for debug
initial
$monitor ("i_add_term1 = %b, i_add_term2 = %b, o_result = %b", i_add_term1, i_add_term2, o_result);
ripple_carry_adder #(.WIDTH(WIDTH))inst_ripple_adder(
.i_add_term1(i_add_term1),
.i_add_term2(i_add_term2),
.o_result(o_result)
);
endmodule
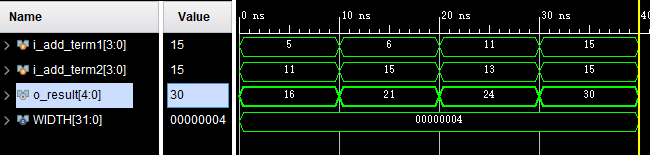
仿真波形:
i_add_term1 = 0101, i_add_term2 = 1011, o_result = 10000
i_add_term1 = 0110, i_add_term2 = 1111, o_result = 10101
i_add_term1 = 1011, i_add_term2 = 1101, o_result = 11000
i_add_term1 = 1111, i_add_term2 = 1111, o_result = 11110
注意事项
- generate for的使用
- 参数化的使用
今天就到这里吧,还没有结束,下一篇文章专门讲解超前进位加法器。
参考资料
-
参考资料1
-
参考资料2
-
参考资料3
交个朋友
-
个人微信公众号:FPGA LAB,左下角二维码;
-
知乎:李锐博恩,右下角二维码。

-
FPGA/IC技术交流2020