- 树链剖分
- 1.算法分析
- 1.1 重链剖分:
- 1.1.1 定义
- 1.1.2 重链剖分的性质
- 1.1.3 常见应用
- 1.2 长链剖分
- 1.2.1 定义
- 1.2.2 长链剖分性质
- 1.2.3 长链剖分应用
- 1.1 重链剖分:
- 2. 板子
- 2.1 重链剖分
- 2.1.1 路径维护/子树维护/lca
- 2.2 长链剖分
- 2.2.1 求lca/求每条长链的长度
- 2.2.2 查询一个点的k级祖先
- 2.2.3 O(n)处理可合并的与深度有关的子树信息
- 2.1 重链剖分
- 3. 例题
- 3.1 重链剖分
- 1.算法分析
树链剖分
1.算法分析
dfs1函数:这里要注意根节点不能设为0,否则根节点的最重链无法更新,始终为0
1.1 重链剖分:
1.1.1 定义
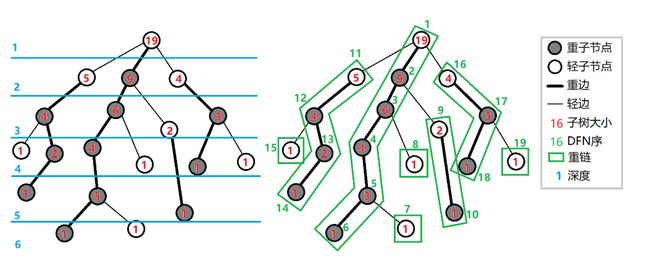
重子节点 表示其子节点中子树最大的子结点。如果有多个子树最大的子结点,取其一。如果没有子节点,就无重子节点。轻子节点 表示剩余的所有子结点。从这个结点到重子节点的边为 重边 。到其他轻子节点的边为 轻边 。若干条首尾衔接的重边构成 重链 。把落单的结点也当作重链,那么整棵树就被剖分成若干条重链。
1.1.2 重链剖分的性质
树上每个节点都属于且仅属于一条重链。 重链开头的结点不一定是重子节点(因为重边是对于每一个结点都有定义的)。所有的重链将整棵树 完全剖分 。在剖分时 优先遍历重儿子 ,最后重链的DFS序就会是连续的。在剖分时,重边优先遍历,最后树的 DFN 序上,重链内的DFN序是连续的。按DFN排序后的序列即为剖分后的链。一颗子树内的 DFN 序是连续的。可以发现,当我们向下经过一条 轻边 时,所在子树的大小至少会除以二。因此,对于树上的任意一条路径,把它拆分成从 分别向两边往下走,分别最多走O(logn)次,因此,树上的每条路径都可以被拆分成不超过 O(logn) 条重链。
1.1.3 常见应用
- 路径维护:用树链剖分求树上两点路径权值和。链上的 DFS 序是连续的,可以使用线段树、树状数组维护。每次选择深度较大的链往上跳,直到两点在同一条链上。同样的跳链结构适用于维护、统计路径上的其他信息。
- 子树维护:维护子树上的信息,譬如将以x为根的子树的所有结点的权值增加v。在 DFS 搜索的时候,子树中的结点的 DFS 序是连续的。每一个结点记录 bottom 表示所在子树连续区间末端的结点。这样就把子树信息转化为连续的一段区间信息。
- 求最近公共祖先:不断向上跳重链,当跳到同一条重链上时,深度较小的结点即为 LCA。
1.2 长链剖分
1.2.1 定义
长链剖分本质上就是另外一种链剖分方式。
定义 重子节点 表示其子节点中子树深度最大的子结点。如果有多个子树最大的子结点,取其一。如果没有子节点,就无重子节点。
定义 轻子节点 表示剩余的子结点。
从这个结点到重子节点的边为 重边 。
到其他轻子节点的边为 轻边 。
若干条首尾衔接的重边构成 重链 。
把落单的结点也当作重链,那么整棵树就被剖分成若干条重链。
如图(这种剖分方式既可以看成重链剖分也可以看成长链剖分):
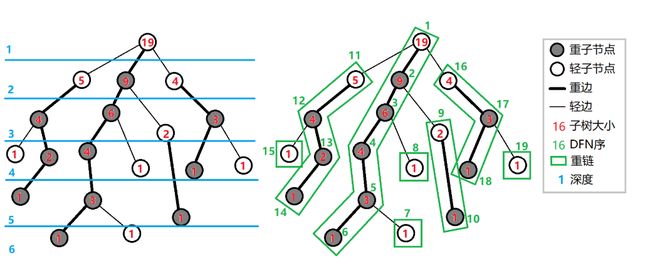
1.2.2 长链剖分性质
- 任意点祖先所在长链长度一点大于等于这个点所在长链长度
- 所有长链长度之和就是总结点数
- 一个点到根节点的路径上经过的短边最多有 √n 条 (长儿子深度和短儿子深度相等时取到)
1.2.3 长链剖分应用
- O(1) 移动到链头 (求lca,和重链剖分一样)
- O(nlogn) 预处理,单次 O(1) 在线查询一个点的 k 级祖先
- O(n) 处理可合并的与深度有关的子树信息 (例如某深度点数、某深度点权和)
2. 板子
2.1 重链剖分
2.1.1 路径维护/子树维护/lca
luogu P3384 【模板】轻重链剖分
一棵包含 N 个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作:
操作 1: 格式: 1 x y z 表示将树从 x 到 y 结点最短路径上所有节点的值都加上 z。
操作 2: 格式: 2 x y 表示求树从 x 到 y 结点最短路径上所有节点的值之和。
操作 3: 格式: 3 x z 表示将以 x 为根节点的子树内所有节点值都加上 z。
操作 4: 格式: 4 x 表示求以 x 为根节点的子树内所有节点值之和
操作有1e5个,树的节点数为1e5个
#include
using namespace std;
const int N=100000+10;
int tot, num;
int n, m, r, p;
int w[N], a[N], dat[N*4], lazy[N*4]; // w[i]=j表示时间戳为i的点的值为j,a[]输入每个节点的值,dat线段树每个点权值,lazy线段树每个点的懒标记
int h[N], e[N*2], ne[N*2], idx; // 邻接表数组
int dep[N], dfn[N], wson[N], size[N], top[N], fa[N]; // dep深度 dfn搜索序 wson重儿子 size子树大小 top链头 fa父节点
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
// 得到size, fa, dep, wson数组
void dfs1(int u)
{
dep[u]=dep[fa[u]]+1;
size[u]=1;
for(int i=h[u]; ~i; i=ne[i])
{#include
using namespace std;
const int N = 100000+10;
int tot, num;
int n, m, r, p;
int w[N], a[N], dat[N * 4], lazy[N * 4]; // w[i]=j表示时间戳为i的点的值为j,a[]输入每个节点的值,dat线段树每个点权值,lazy线段树每个点的懒标记
int h[N], e[N * 2], ne[N * 2], idx; // 邻接表数组
int dep[N], dfn[N], wson[N], sz[N], top[N], fa[N]; // dep深度 dfn搜索序 wson重儿子 size子树大小 top链头 fa父节点
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
// 得到sz, fa, dep, wson数组
void dfs1(int u)
{
dep[u] = dep[fa[u]]+1;
sz[u] = 1;
for(int i = h[u]; ~i; i = ne[i])
{
int j=e[i];
if(j == fa[u]) continue;
fa[j] = u;
dfs1(j);
sz[u] += sz[j];
if(sz[j] > sz[wson[u]]) wson[u] = j; // 这里要注意根节点不能设为0,否则根节点的最重链无法更新,始终为0
}
}
// 得到dfn, top数组
void dfs2(int u, int nowtop)
{
dfn[u] = ++num;
w[num] = a[u];
//以搜索序重排权值
top[u] = nowtop;
if(wson[u]) dfs2(wson[u], nowtop); // 先搜索重儿子
for(int i = h[u]; ~i; i = ne[i]) // 然后搜索轻儿子
{
int y=e[i];
if(y ==fa[u]||y == wson[u]) continue;
dfs2(y, y);
}
}
void pushup(int rt) {
dat[rt] = dat[rt << 1] + dat[rt << 1 | 1];
dat[rt] %= p;
}
// 建线段树,rt为根,l为rt点管辖的左边界, r为rt点管辖的有边界
void build(int rt, int l, int r)
{
if(l==r)
{
dat[rt]=w[l];
return ;
}
int mid=(l + r)>>1;
build(rt << 1, l, mid);
build(rt << 1 | 1, mid+1, r);
pushup(rt);
}
// 下传
void pushdown(int rt, int l, int r)
{
if(lazy[rt])
{
int mid=(l + r)>>1;
dat[rt << 1] += lazy[rt]*(mid - l + 1), dat[rt << 1] %= p, lazy[rt << 1] += lazy[rt];
dat[rt << 1 | 1] += lazy[rt]*(r-mid), dat[rt << 1 | 1] %= p, lazy[rt << 1 | 1] += lazy[rt];
lazy[rt]=0;
}
}
// rt为根,l为rt点管辖的左边界, r为rt点管辖的有边界, l为需要修改的左区间,r为需要修改的右区间
void modify(int rt, int l, int r, int L, int R, int k)
{
if(L <= l && r <= R)
{
dat[rt] += k*(r-l+1);
dat[rt] %= p;
lazy[rt] += k;
lazy[rt] %= p;
return ;
}
pushdown(rt, l, r);
int mid = (l + r)>>1;
if(L <= mid) modify(rt << 1, l, mid, L, R, k);
if(mid < R) modify(rt << 1 | 1, mid + 1, r, L, R, k);
pushup(rt);
}
// rt为根,l为rt点管辖的左边界, r为rt点管辖的有边界, l为需要查询的左区间,r为查询的右区间
int query(int rt, int l, int r, int L, int R)
{
if(L <= l && r <= R)
{
return dat[rt];
}
pushdown(rt, l, r);
int mid = (l + r)>>1;
int ans = 0;
if(L <= mid) ans += query(rt << 1, l, mid, L, R), ans %= p;
if(mid < R) ans += query(rt << 1 | 1, mid + 1, r, L, R), ans %= p;
return ans;
}
// 求树从 x 到 y 结点最短路径上所有节点的值之和
int path_query_Tree(int x, int y)
{
//两点间的修改
int ans = 0;
while(top[x] != top[y]) // 把x点和y点整到一条重链上
{
if(dep[top[x]] < dep[top[y]]) swap(x, y); // 让x点为深的那个点
ans += query(1, 1, n, dfn[top[x]], dfn[x]);
ans %= p;
x = fa[top[x]]; // x每次跳一条链
}
if(dep[x] > dep[y]) swap(x, y); // 让x成为深度更浅的那个点
ans += query(1, 1, n, dfn[x], dfn[y]);
return ans % p;
}
// 将树从 x到 y 结点最短路径上所有节点的值都加上 z
void path_modify_Tree(int x, int y, int k)
{
//树上两点距离
k %= p;
while(top[x] != top[y]) // 把x点和y点整到一条重链上
{
if(dep[top[x]] < dep[top[y]]) swap(x, y); // 让x成为对应的头部深度更大的那个点
modify(1, 1, n, dfn[top[x]], dfn[x], k); // 累加x的所有子树和
x = fa[top[x]]; // x跳到原来x的头部的父节点
}
if(dep[x] > dep[y]) swap(x, y); // 让x成为深度更浅的那个点
modify(1, 1, n, dfn[x], dfn[y], k);
}
// 求以 x 为根节点的子树内所有节点值之和
int Point_query_Tree(int rt)
{
//由搜索序的特点可得,子树的搜索序一定比根大
return query(1, 1, n, dfn[rt], dfn[rt]+sz[rt]-1);
}
// 将以 x 为根节点的子树内所有节点值都加上 z
void Point_modify_Tree(int rt, int k)
{
k %= p;
modify(1, 1, n, dfn[rt], dfn[rt]+sz[rt]-1, k);
}
// 求u和v的lca
int lca(int u, int v)
{
while (top[u] != top[v])
{
if (dep[top[u]] > dep[top[v]])
u = fa[top[u]];
else
v = fa[top[v]];
}
return dep[u] > dep[v] ? v : u;
}
int main()
{
scanf("%d%d%d%d", &n, &m, &r, &p); // 读入点数、边数、根、模数
for(int i=1; i<=n; i++) scanf("%d", &a[i]); // 读入每个点的权值
// 读入边,建树
memset(h, -1, sizeof h);
for(int i=1, x, y; i lugou P2486 [SDOI2011]染色
题意:
给定一棵 n 个节点的无根树,共有 m 个操作,操作分为两种:
- 将节点 aa 到节点 bb 的路径上的所有点(包括 aa 和 bb)都染成颜色 cc。
- 询问节点 aa 到节点 bb 的路径上的颜色段数量。
颜色段的定义是极长的连续相同颜色被认为是一段。例如 112221 由三段组成:11、222、1。
题解: 线段树+树剖,线段树维护颜色信息即可
以下代码没有调通
#include
using namespace std;
const int N=1e5 + 10;
int tot, num;
int n, m, r;
int w[N], a[N], lco[N * 4], rco[N * 4], dat[N*4], lazy[N*4]; // w[i]=j表示时间戳为i的点的值为j,a[]输入每个节点的值,dat线段树每个点权值,lazy线段树每个点的懒标记
int h[N], e[N*2], ne[N*2], idx; // 邻接表数组
int dep[N], dfn[N], wson[N], sz[N], top[N], fa[N]; // dep深度 dfn搜索序 wson重儿子 sz子树大小 top链头 fa父节点
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
// 得到sz, fa, dep, wson数组
void dfs1(int u)
{
dep[u] = dep[fa[u]] + 1;
sz[u] = 1;
for(int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if(j == fa[u]) continue;
fa[j] = u;
dfs1(j);
sz[u] += sz[j];
if(sz[j] > sz[wson[u]]) wson[u]=j; // 这里要注意根节点不能设为0,否则根节点的最重链无法更新,始终为0
}
}
// 得到dfn, top数组
void dfs2(int u, int nowtop)
{
dfn[u] = ++num;
w[num] = a[u];
//以搜索序重排权值
top[u] = nowtop;
if(wson[u]) dfs2(wson[u], nowtop); // 先搜索重儿子
for(int i = h[u]; ~i; i = ne[i]) // 然后搜索轻儿子
{
int y = e[i];
if(y == fa[u] || y == wson[u]) continue;
dfs2(y, y);
}
}
void pushup(int rt) {
lco[rt] = lco[rt << 1] , rco[rt] = lco[rt << 1 | 1];
dat[rt] = dat[rt << 1] + dat[rt << 1 | 1];
if (rco[rt << 1] == lco[rt << 1 | 1]) dat[rt]--;
}
// 建线段树,rt为根,l为rt点管辖的左边界, r为rt点管辖的有边界
void build(int rt, int l, int r)
{
if(l == r)
{
dat[rt] = 1;
lco[rt] = rco[rt] = w[l];
lazy[rt] = 0;
return ;
}
int mid = (l + r) >> 1;
build(rt << 1, l, mid);
build(rt << 1 | 1, mid + 1, r);
pushup(rt);
}
void pushdown(int rt, int l, int r) {
if (lazy[rt]) {
lazy[rt << 1] = lazy[rt];
lazy[rt << 1 | 1] = lazy[rt];
lco[rt << 1] = rco[rt << 1] = lazy[rt];
lco[rt << 1 | 1] = rco[rt << 1 | 1] = lazy[rt];
dat[rt << 1] = 1;
dat[rt << 1 | 1] = 1;
lazy[rt] = 0;
}
}
void modify(int rt, int l, int r, int L, int R, int c) {
if (L <= l && r <= R) {
dat[rt] = 1;
lco[rt] = rco[rt] = c;
lazy[rt] = c;
return;
}
pushdown(rt, l, r);
int mid = (l + r) >> 1;
if (L <= mid) modify(rt << 1, l, mid, L, R, c);
if (mid < R) modify(rt << 1 | 1, mid + 1, r, L, R, c);
pushup(rt);
}
int query(int rt, int l, int r, int L, int R) {
if (L <= l && r <= R) return dat[rt];
pushdown(rt, l, r);
int mid = (l + r) >> 1;
int res = 0, flg = 0;
if (L <= mid) {
res = query(rt << 1, l, mid, L, R), flg = 1;
}
if (mid < R) {
res += query(rt << 1 | 1, mid + 1, r, L, R);
if (flg == 1 && rco[rt << 1] == lco[rt << 1 | 1]) res--;
}
return res;
}
// 求树从 x 到 y 结点最短路径上所有节点的值之和
int path_query_Tree(int x, int y)
{
//两点间的修改
int ans = 0;
while(top[x] != top[y]) // 把x点和y点整到一条重链上
{
if(dep[top[x]] < dep[top[y]]) swap(x, y); // 让x点为深的那个点
ans += query(1, 1, n, dfn[top[x]], dfn[x]);
if (a[top[x]] == a[fa[top[x]]]) ans--;
x = fa[top[x]]; // x每次跳一条链
}
if(dep[x] > dep[y]) swap(x, y); // 让x成为深度更浅的那个点
ans += query(1, 1, n, dfn[x], dfn[y]);
return ans;
}
// 将树从 x到 y 结点最短路径上所有节点的值都加上 z
void path_modify_Tree(int x, int y, int k)
{
//树上两点距离
while(top[x] != top[y]) // 把x点和y点整到一条重链上
{
if(dep[top[x]] < dep[top[y]]) swap(x, y); // 让x成为对应的头部深度更大的那个点
modify(1, 1, n, dfn[top[x]], dfn[x], k); // 累加x的所有子树和
x = fa[top[x]]; // x跳到原来x的头部的父节点
}
if(dep[x] > dep[y]) swap(x, y); // 让x成为深度更浅的那个点
modify(1, 1, n, dfn[x], dfn[y], k);
}
int main()
{
scanf("%d%d", &n, &m); // 读入点数、边数、根、模数
r = 1;
for(int i = 1; i <= n; i++) scanf("%d", &a[i]); // 读入每个点的权值
// 读入边,建树
memset(h, -1, sizeof h);
for(int i = 1, x, y; i < n; i++)
{
scanf("%d%d", &x, &y);
add(x, y);
add(y, x);
}
// 两次dfs把树按照重链剖分
dfs1(r); // 得到sz, fa, dep, wson数组
dfs2(r, r); // 得到dfn, top数组
build(1, 1, n);
// m次询问
string op;
for(int i = 1, x, y, z; i <= m; i++)
{
cin >> op;
if (op[0] == 'Q') {
scanf("%d %d", &x, &y);
printf("%d\n", path_query_Tree(x, y));
}
else {
scanf("%d%d%d", &x, &y, &z);
path_modify_Tree(x, y, z);
}
}
return 0;
} 2.2 长链剖分
2.2.1 求lca/求每条长链的长度
求lca
#include
using namespace std;
const int N=500000+10;
int lson[N], maxlen[N], fa[N], dep[N], top[N]; // lso长儿子,maxlen最大深度,fa父节点,dep深度,top链头
int h[N],e[N*2],ne[N*2], idx;
int n, m, root;
void add(int a,int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
// 求fa,dep, maxlen
void dfs1(int x)
{
dep[x]=dep[fa[x]]+1;
maxlen[x]=dep[x];
for(int i=h[x];~i;i=ne[i])
{
int y=e[i];
if(y!=fa[x])
{
fa[y]=x;
dfs1(y);
maxlen[x]=max(maxlen[y],maxlen[x]);
if(maxlen[y]>maxlen[lson[x]]) lson[x]=y; // 这里要注意根节点不能设为0,否则根节点的最长链无法更新,始终为0
}
}
}
// 求top
void dfs2(int x,int nowtop)
{
top[x]=nowtop;
if(lson[x]) dfs2(lson[x],nowtop);
for(int i=h[x];~i;i=ne[i])
{
int y=e[i];
if(y!=fa[x]&&y!=lson[x]) dfs2(y,y);
}
}
// 求lca
int lca(int x,int y)
{
while(top[x]!=top[y])
{
if(dep[top[x]] Benelux Algorithm Programming Contest 2019
A. Appeal to the Audience
题意: 给定一棵n点树,该树有m叶,每片叶子都有权值k,每片叶子能带来叶子所处的长链的长度*叶子权值k的收益,求最大收益。
题解: 长链的贪心性质
代码:
/*
本题需要让越大权值的运动员位于越长的链的底部,即可求出最大答案
只需要多维护一个数组len,记录每条链的长度即可
*/
#include
using namespace std;
typedef long long LL;
const int N=100000+10;
int lson[N], maxlen[N], fa[N], dep[N], top[N]; // lso长儿子,maxlen最大深度,fa父节点,dep深度,top链头
int h[N],e[N*2],ne[N*2], idx;
int n, m, root;
int a[N], len[N]; // len维护每一条链的长度
void add(int a,int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
// 求fa,dep, maxlen
void dfs1(int x)
{
dep[x]=dep[fa[x]]+1;
maxlen[x]=dep[x];
for(int i=h[x];~i;i=ne[i])
{
int y=e[i];
if(y!=fa[x])
{
fa[y]=x;
dfs1(y);
maxlen[x]=max(maxlen[y],maxlen[x]);
if(maxlen[y]>maxlen[lson[x]]) lson[x]=y;
}
}
}
// 求top
void dfs2(int x,int nowtop, int length)
{
top[x]=nowtop;
len[nowtop] = length + 1; // 链头为nowtop的链的长度为length+1
if(lson[x]) dfs2(lson[x],nowtop, len[nowtop]);
for(int i=h[x];~i;i=ne[i])
{
int y=e[i];
if(y!=fa[x]&&y!=lson[x]) dfs2(y,y, 0);
}
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= m; ++i) scanf("%d", &a[i]);
sort(a + 1, a + 1 + m);
reverse(a + 1, a + 1 + m);
memset(h, -1, sizeof h);
for(int i=2, x;i<=n;++i)
{
cin >> x;
x++;
add(i, x), add(x, i);
}
root = 1;
dfs1(root); // 第一次求dep, fa, maxlen, lson
dfs2(root,root, 0); // 第二次求top
set s;
for (int i = 1; i <= n; ++i) s.insert(top[i]);
LL ans = 0;
int i = 0;
vector v;
for (auto si: s) v.push_back(len[si]);
sort(v.begin(), v.end());
reverse(v.begin(), v.end());
for (int i = 0; i < m; ++i)
{
if (i == 0) v[i]--;
ans += a[i + 1] * (LL)(v[i]);
}
cout << ans << endl;
return 0;
} 2.2.2 查询一个点的k级祖先
2.2.3 O(n)处理可合并的与深度有关的子树信息
3. 例题
3.1 重链剖分
P2590 [ZJOI2008]树的统计
题意:
一棵树上有 n 个节点,编号分别为 1 到 n,每个节点都有一个权值 w。
我们将以下面的形式来要求你对这棵树完成一些操作:
I. CHANGE u t : 把结点 u 的权值改为 t。
II. QMAX u v: 询问从点 u 到点 v 的路径上的节点的最大权值。
III. QSUM u v: 询问从点 u 到点 v 的路径上的节点的权值和。
注意:从点 u 到点 v 的路径上的节点包括 u 和 v 本身。
题解:
只需要线段树加单点修改区间查询的线段树即可,模板题
代码:
#include
using namespace std;
const int N = 3e4 + 10, INF = 1e9 + 10;
int tot, num;
int n, m, r;
// dat1:sum, dat2:max
int w[N], a[N], dat1[N * 4], dat2[N * 4]; // w[i]=j表示时间戳为i的点的值为j,a[]输入每个节点的值,dat线段树每个点权值,lazy线段树每个点的懒标记
int h[N], e[N * 2], ne[N * 2], idx; // 邻接表数组
int dep[N], dfn[N], wson[N], sz[N], top[N], fa[N]; // dep深度 dfn搜索序 wson重儿子 size子树大小 top链头 fa父节点
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
// 得到sz, fa, dep, wson数组
void dfs1(int u)
{
dep[u] = dep[fa[u]] + 1;
sz[u] = 1;
for(int i = h[u]; ~i; i = ne[i])
{
int j=e[i];
if(j == fa[u]) continue;
fa[j] = u;
dfs1(j);
sz[u] += sz[j];
if(sz[j] > sz[wson[u]]) wson[u] = j; // 这里要注意根节点不能设为0,否则根节点的最重链无法更新,始终为0
}
}
// 得到dfn, top数组
void dfs2(int u, int nowtop)
{
dfn[u] = ++num;
w[num] = a[u];
//以搜索序重排权值
top[u] = nowtop;
if(wson[u]) dfs2(wson[u], nowtop); // 先搜索重儿子
for(int i = h[u]; ~i; i = ne[i]) // 然后搜索轻儿子
{
int y = e[i];
if(y == fa[u] || y == wson[u]) continue;
dfs2(y, y);
}
}
void pushup(int rt) {
dat1[rt] = dat1[rt << 1] + dat1[rt << 1 | 1];
dat2[rt] = max(dat2[rt << 1], dat2[rt << 1 | 1]);
}
// 建线段树,rt为根,l为rt点管辖的左边界, r为rt点管辖的有边界
void build(int rt, int l, int r)
{
if(l == r)
{
dat1[rt] = dat2[rt] = w[l];
return ;
}
int mid = (l + r) >> 1;
build(rt << 1, l, mid);
build(rt << 1 | 1, mid+1, r);
pushup(rt);
}
void modify(int rt, int l, int r, int x, int y) {
if (l == r) {
dat1[rt] = y;
dat2[rt] = y;
return;
}
int mid = (l + r) >> 1;
if (x <= mid) modify(rt << 1, l, mid, x, y);
else modify(rt << 1 | 1, mid + 1, r, x, y);
pushup(rt);
}
int query1(int rt, int l, int r, int L, int R)
{
if(L <= l && r <= R) return dat1[rt];
int mid = (l + r)>>1;
int ans = 0;
if(L <= mid) ans += query1(rt << 1, l, mid, L, R);
if(mid < R) ans += query1(rt << 1 | 1, mid + 1, r, L, R);
return ans;
}
int query2(int rt, int l, int r, int L, int R) {
if (L <= l && r <= R) return dat2[rt];
int mid = (l + r) >> 1;
int ans = -INF;
if (L <= mid) ans = max(ans, query2(rt << 1, l, mid, L, R));
if (mid < R) ans = max(ans, query2(rt << 1 | 1, mid + 1, r, L, R));
return ans;
}
// 求树从 x 到 y 结点最短路径上所有节点的值之和
int path_query_Tree1(int x, int y)
{
//两点间的修改
int ans = 0;
while(top[x] != top[y]) // 把x点和y点整到一条重链上
{
if(dep[top[x]] < dep[top[y]]) swap(x, y); // 让x点为深的那个点
ans += query1(1, 1, n, dfn[top[x]], dfn[x]);
x = fa[top[x]]; // x每次跳一条链
}
if(dep[x] > dep[y]) swap(x, y); // 让x成为深度更浅的那个点
ans += query1(1, 1, n, dfn[x], dfn[y]);
return ans;
}
// 求树从 x 到 y 结点最短路径上所有节点的max
int path_query_Tree2(int x, int y)
{
//两点间的修改
int ans = -INF;
while(top[x] != top[y]) // 把x点和y点整到一条重链上
{
if(dep[top[x]] < dep[top[y]]) swap(x, y); // 让x点为深的那个点
ans = max(ans, query2(1, 1, n, dfn[top[x]], dfn[x]));
x = fa[top[x]]; // x每次跳一条链
}
if(dep[x] > dep[y]) swap(x, y); // 让x成为深度更浅的那个点
ans = max(ans, query2(1, 1, n, dfn[x], dfn[y]));
return ans;
}
void modify_Tree(int x, int y) {
modify(1, 1, n, dfn[x], y);
}
int main()
{
scanf("%d", &n); // 读入点数、边数、根、模数
r = 1;
// 读入边,建树
memset(h, -1, sizeof h);
for(int i = 1, x, y; i < n; i++)
{
scanf("%d%d", &x, &y);
add(x, y);
add(y, x);
}
for(int i = 1; i <= n; i++) scanf("%d", &a[i]); // 读入每个点的权值
scanf("%d", &m);
// 两次dfs把树按照重链剖分
dfs1(r); // 得到sz, fa, dep, wson数组
dfs2(r, r); // 得到dfn, top数组
build(1, 1, n);
// m次询问
for(int i=1, u, v; i<=m; i++)
{
char op[10];
scanf("%s", op);
scanf("%d%d", &u, &v);
if (op[0] == 'Q' && op[1] == 'S') printf("%d\n", path_query_Tree1(u, v));
else if (op[0] == 'Q' && op[1] == 'M') printf("%d\n", path_query_Tree2(u, v));
else modify_Tree(u, v);
}
return 0;
} P2146 [NOI2015]软件包管理器
题意:
你决定设计你自己的软件包管理器。不可避免地,你要解决软件包之间的依赖问题。如果软件包 a 依赖软件包 b,那么安装软件包 a 以前,必须先安装软件包 b。同时,如果想要卸载软件包 b,则必须卸载软件包 a。
现在你已经获得了所有的软件包之间的依赖关系。而且,由于你之前的工作,除 0 号软件包以外,在你的管理器当中的软件包都会依赖一个且仅一个软件包,而 0 号软件包不依赖任何一个软件包。且依赖关系不存在环
现在你要为你的软件包管理器写一个依赖解决程序。根据反馈,用户希望在安装和卸载某个软件包时,快速地知道这个操作实际上会改变多少个软件包的安装状态(即安装操作会安装多少个未安装的软件包,或卸载操作会卸载多少个已安装的软件包),你的任务就是实现这个部分。
注意,安装一个已安装的软件包,或卸载一个未安装的软件包,都不会改变任何软件包的安装状态,即在此情况下,改变安装状态的软件包数为 0。
题解: 通过分析可以知道软件依赖关系是一棵树,当安装软件时,就是影响从根(0节点)到x;当卸载软件时,就是影响以x为根的子树。所以只需要线段树lazy维护区间染色,dat维护区间和即可。
代码:
#include
using namespace std;
const int N = 1e5 + 10;
int tot, num;
int n, m, r;
int w[N], a[N], dat[N * 4], lazy[N * 4]; // w[i]=j表示时间戳为i的点的值为j,a[]输入每个节点的值,dat线段树每个点权值,lazy线段树每个点的懒标记
int h[N], e[N * 2], ne[N * 2], idx; // 邻接表数组
int dep[N], dfn[N], wson[N], sz[N], top[N], fa[N]; // dep深度 dfn搜索序 wson重儿子 size子树大小 top链头 fa父节点
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
// 得到sz, fa, dep, wson数组
void dfs1(int u)
{
dep[u] = dep[fa[u]]+1;
sz[u] = 1;
for(int i = h[u]; ~i; i = ne[i])
{
int j=e[i];
if(j == fa[u]) continue;
fa[j] = u;
dfs1(j);
sz[u] += sz[j];
if(sz[j] > sz[wson[u]]) wson[u] = j; // 这里要注意根节点不能设为0,否则根节点的最重链无法更新,始终为0
}
}
// 得到dfn, top数组
void dfs2(int u, int nowtop)
{
dfn[u] = ++num;
w[num] = a[u];
//以搜索序重排权值
top[u] = nowtop;
if(wson[u]) dfs2(wson[u], nowtop); // 先搜索重儿子
for(int i = h[u]; ~i; i = ne[i]) // 然后搜索轻儿子
{
int y=e[i];
if(y ==fa[u]||y == wson[u]) continue;
dfs2(y, y);
}
}
void pushup(int rt) {
dat[rt] = dat[rt << 1] + dat[rt << 1 | 1];
}
// 建线段树,rt为根,l为rt点管辖的左边界, r为rt点管辖的有边界
void build(int rt, int l, int r)
{
if(l==r)
{
dat[rt] = 0;
lazy[rt] = -1;
return ;
}
int mid=(l + r)>>1;
build(rt << 1, l, mid);
build(rt << 1 | 1, mid+1, r);
pushup(rt);
}
// 下传
void pushdown(int rt, int l, int r)
{
if (lazy[rt] == -1) return;
int mid=(l + r)>>1;
dat[rt << 1] = lazy[rt]*(mid - l + 1), lazy[rt << 1] = lazy[rt];
dat[rt << 1 | 1] = lazy[rt]*(r-mid), lazy[rt << 1 | 1] = lazy[rt];
lazy[rt]=-1;
}
// rt为根,l为rt点管辖的左边界, r为rt点管辖的有边界, l为需要修改的左区间,r为需要修改的右区间
void modify(int rt, int l, int r, int L, int R, int k)
{
if(L <= l && r <= R)
{
dat[rt] = k*(r-l+1);
lazy[rt] = k;
return ;
}
pushdown(rt, l, r);
int mid = (l + r)>>1;
if(L <= mid) modify(rt << 1, l, mid, L, R, k);
if(mid < R) modify(rt << 1 | 1, mid + 1, r, L, R, k);
pushup(rt);
}
// rt为根,l为rt点管辖的左边界, r为rt点管辖的有边界, l为需要查询的左区间,r为查询的右区间
int query(int rt, int l, int r, int L, int R)
{
if(L <= l && r <= R)
{
return dat[rt];
}
pushdown(rt, l, r);
int mid = (l + r)>>1;
int ans = 0;
if(L <= mid) ans += query(rt << 1, l, mid, L, R);
if(mid < R) ans += query(rt << 1 | 1, mid + 1, r, L, R);
return ans;
}
// 求树从 x 到 y 结点最短路径上所有节点的值之和
int path_query_Tree(int x, int y)
{
//两点间的修改
int ans = 0;
while(top[x] != top[y]) // 把x点和y点整到一条重链上
{
if(dep[top[x]] < dep[top[y]]) swap(x, y); // 让x点为深的那个点
ans += query(1, 1, n, dfn[top[x]], dfn[x]);
x = fa[top[x]]; // x每次跳一条链
}
if(dep[x] > dep[y]) swap(x, y); // 让x成为深度更浅的那个点
ans += query(1, 1, n, dfn[x], dfn[y]);
return ans;
}
// 将树从 x到 y 结点最短路径上所有节点的值都赋值为 z
void path_modify_Tree(int x, int y, int k)
{
//树上两点距离
while(top[x] != top[y]) // 把x点和y点整到一条重链上
{
if(dep[top[x]] < dep[top[y]]) swap(x, y); // 让x成为对应的头部深度更大的那个点
modify(1, 1, n, dfn[top[x]], dfn[x], k); // 累加x的所有子树和
x = fa[top[x]]; // x跳到原来x的头部的父节点
}
if(dep[x] > dep[y]) swap(x, y); // 让x成为深度更浅的那个点
modify(1, 1, n, dfn[x], dfn[y], k);
}
// 求以 x 为根节点的子树内所有节点值之和
int Point_query_Tree(int rt)
{
//由搜索序的特点可得,子树的搜索序一定比根大
return query(1, 1, n, dfn[rt], dfn[rt]+sz[rt]-1);
}
void Point_modify_Tree(int rt, int k)
{
modify(1, 1, n, dfn[rt], dfn[rt]+sz[rt]-1, k);
}
int main()
{
scanf("%d", &n);
r = 1;
// 读入边,建树
memset(h, -1, sizeof h);
for (int i = 2, x; i <= n; ++i) {
scanf("%d", &x);
x++;
add(i, x), add(x, i);
}
scanf("%d", &m);
// 两次dfs把树按照重链剖分
dfs1(r); // 得到sz, fa, dep, wson数组
dfs2(r, r); // 得到dfn, top数组
build(1, 1, n);
// m次询问
char op[10];
for(int i=1, x; i<=m; i++)
{
scanf("%s", op);
scanf("%d", &x);
x++;
if(op[0] == 'i')
{
int cnt1 = path_query_Tree(1, x);
path_modify_Tree(1, x, 1);
printf("%d\n", path_query_Tree(1, x) - cnt1);
}
else
{
int cnt1 = Point_query_Tree(x);
Point_modify_Tree(x, 0);
printf("%d\n", cnt1); //求树从 x 到 y 结点最短路径上所有节点的值之和
}
}
return 0;
}