最短路

最短路

1. 算法分析

1.1 图论最短/长路模型

1. 单源最短/长路问题

   • dijkstra朴素版本求最短路 (O(n^2^)):适合稠密图，用邻接矩阵存储，不能处理有负权边情况
   • dijkstra堆优化版本求最短路 (O(mlogn)):与边数有关，适合稀疏图，使用邻接表存储，不能处理有负权边情况
   • dijkstra双端队列优化版本求最短路 O(m+n):边权为01特殊情况
   • dijkstra有条件约束求最短路 (O(mlogn)):补充一个数组作为约束条件
   • bellman_ford求最短路 (O(nm)):可以处理最多经过k条边的题目，可以处理负权边，但因为时间复杂度较高，一般被spfa替代
   • spfa求最短路 O(km),最坏复杂度可以到O(nm),可被网格图卡，可以处理负权边
   • spfa求最长路:最短路变化版本
   • bfs最短路模型求最短路 O(m + n): 只能处理边权为1的情况
   • 拓扑排序模型求最短路 O(m+n):必须为DAG

2. 多源最短路问题

   • floyd最短路问题 O(n^3)
   • floyd传递闭包问题 O(n^3)
   • floyd找有向/无向最小环 O(n^3)
   • floyd找恰好经过k条的最短距离

3. 最短路计数模型

4. 次短路模型与k短路模型

1.2 图论建模技巧

1. 把多源转化为单源: 建立一个虚拟源点，该虚拟源点向每个点建立一条权值为0的边
2. dp转化最短路求解:如果使用dp求解存在环，那么必须转化为最短路问题求解
3. 最短路转换为dp求解:如果能够得到一张图的拓扑序，沿着拓扑序dp更新即可得到最短路/最长路
4. 分层建图
5. 二分图建图优化建图
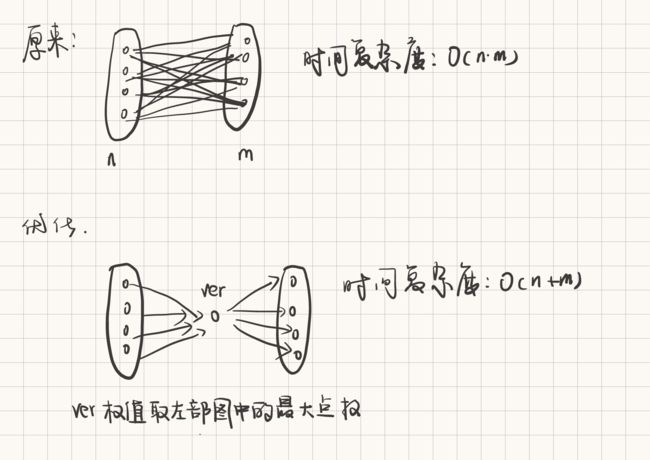
       对于一个二分图，左边的每个点都需要向右边每个点连一条边的建图模型来说，可以设置一个虚拟节点，然后使得左边每个点连向虚拟节点，虚拟节点再向右边每个点连边。这样就把O(n ^ 2)优化到O(n)。
   

特点备注

1. 朴素版dijkstra和双端队列bfs、堆优化版dijkstra需要st数组来标记，这个数组标记的是某个点是否使用过；spfa也需要st数组来标记，不过标记的是这个点是否在队列里面；
2. dijkstra、bfs不能处理负权边。spfa、bellman-ford、floyd可以
3. bfs求最短路、dijkstra求最短路对于每个点来说，具有拓扑序；spfa求最短路对于点来说，不具有拓扑序。(spfa每个点出入队列多次，而dijkstra、bfs只出入队一次)

2. 板子

2.1 dijkstra朴素版本求最短路 (O(n2)):适合稠密图，用邻接矩阵存储，不能处理有负权边情况

#include 

using namespace std;

int const N = 510;
int mp[N][N], n, m, dis[N], st[N];  // mp维护两个点之间的距离，dis维护每个点到源点的距离，st[i]表示i点是否在S集合内(i点是否更新过)，如果更新过那么st[i]=1

// dijkstra求最短路
int dijkstra() {
    memset(dis, 0x3f, sizeof dis);  // 初始每个点到源点距离都是无穷远
    dis[1] = 0;  // 把源点加入S集合
    for (int i = 1; i < n; ++i) {  // 需要进行n-1个回合，每个回合选出一个到源点最近的点，然后更新其他点到源点的距离
        int t = -1;  // 到源点最短距离的点为t
        for (int j = 1; j <= n; ++j) // 遍历n个点
            if (!st[j] && (t == -1 || dis[j] < dis[t])) t = j;  // 第一次找到的就是源点
        st[t] = 1;  // 放入S集合
        for (int j = 1; j <= n; ++j) dis[j] = min(dis[j], dis[t] + mp[t][j]);  // 更新其他点到源点的距离，dijkstra保证了每次放入S集合的点是所有点中到源点距离最近的点
    }
    return dis[n] != 0x3f3f3f3f? dis[n]: -1;  // 需要特判无解的情况
}

int main() {
    cin >> n >> m;
    memset(mp, 0x3f, sizeof mp);  // 初始更新每个点间距离为无穷远
    for (int i = 1, a, b, c; i <= m; ++i) {
        scanf("%d%d%d", &a, &b, &c);
        mp[a][b] = min(mp[a][b], c);  // 防止重边，取最小
    }
    cout << dijkstra();
    return 0;
}

2.2 dijkstra堆优化版本求最短路 (O(mlogn)):与边数有关，适合稀疏图，使用邻接表存储，不能处理有负权边情况

#include

using namespace std;

typedef pair PII;
int const N = 2e5 + 10;
int e[N], ne[N],w[N], h[N], idx, n, m, dis[N], st[N];

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

// 堆优化版dijksyta
int dijkstra() {
    memset(dis, 0x3f, sizeof dis);  // 初始化距离为无穷
    priority_queue, greater > q;  // 定义一个按照距离从小到大排序的优先队列，第一维:距离，第二维:点
    dis[1] = 0;  // 一开始源点距离为0
    q.push({0, 1});  // 把源点信息放入队列
    while (q.size()) {  // 每个点只出入队列一次
        auto t = q.top();
        q.pop();
        
        int distance = t.first, ver = t.second;  // 最小距离和相对应的点
        if (st[ver]) continue;  // 这个操作保证每个点只出入队一次，因为队列里面可能会出现{dis1[3], 3}, {dis2[3], 3}的情况，这样保证dis1[3] distance + w[i]) {
                dis[j] = distance + w[i];
                q.push({dis[j], j});  // 这里不需要判断st，因为一旦更新发现更小必须放入队列
            }
        }
    }
    return dis[n] != 0x3f3f3f3f? dis[n]: -1;
}

int main() {
    cin >> n >> m;
    memset(h, -1, sizeof h);  
    for (int i = 1, a, b, c; i <= m; ++i) {  // 读入m条边
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
    }
    cout << dijkstra();
    return 0;
}

2.3 dijkstra双端队列优化版本求最短路 O(m+n):边权为01特殊情况

#include 

using namespace std;

typedef pair PII;
int const N = 110;
int e[N * N], ne[N * N], h[N], w[N * N], idx, n, S, E, dis[N], st[N];

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

// 双端队列优化dijkstra
int dijkstra() {
    memset(dis, 0x3f, sizeof dis);  // 初始化距离为无穷
    deque q;  // 定义一个双端队列
    dis[S] = 0;  // 一开始源点距离为0
    q.push_back({0, S});  // 把源点信息放入队列
    while (q.size()) {  // 每个点只出入队列一次
        auto t = q.front();
        q.pop_front();
        
        int distance = t.first, ver = t.second;  // 最小距离和相对应的点
        if (st[ver]) continue;  // 这个操作保证每个点只出入队一次，因为队列里面可能会出现{dis1[3], 3}, {dis2[3], 3}的情况，这样保证dis1[3] distance + w[i]) {  // 如果能够更新
                dis[j] = distance + w[i];
                if (w[i] == 1) q.push_back({dis[j], j});  // 如果边权为1，那么插入队尾
                else q.push_front({dis[j], j});  // 如果边权为0，那么插入队头
            }
        }
    }
    return dis[E] != 0x3f3f3f3f? dis[E]: -1;
}

int main() {
    memset(h, -1, sizeof h);
    cin >> n >> S >> E;
    
    // 建图
    for (int i = 1, k; i <= n; ++i) {  
        scanf("%d", &k);
        for (int j = 1, t; j <= k; ++j) {  // 读入相邻的点
            scanf("%d", &t);
            add(i, t, (j == 1? 0: 1));  // 如果是第1个点，那么边权为0，其他店点的边权为1
        }
    }
    cout << dijkstra();
    return 0;
}

2.4 dijkstra有条件约束求最短路 (O(mlogn)):补充一个数组作为约束条件

#include 

using namespace std;
typedef long long LL;
int const N = 1100, M = 110;
LL const INF = 0x3f3f3f3f3f3f3f3f;
// dis[i][j]:走到i点限制条件为j时的最小距离，st[i][j]：在i点且限制条件为j是否走到过， w1:边权，w2:限制条件
LL C[M], e[N * N], ne[N * N], w1[N * N], w2[N * N], idx, h[N], dis[N][110], st[N][110];  
struct NODE {
    LL point, distance, strict;  // point:点，distance:最小距离，strict:限制条件
    bool operator<(const NODE &w) const {  // 按照距离的排序，小的排在前面
        return distance > w.distance;
    }
}node[N];  // 放在优先队列内的数据结构
struct POINT {  
    int id, x, y;
}point[N];  // 0~n-1为中间站点，n为起点，n+1为终点
struct PATH {
    int id1, id2, c;
};  // 记录id1->id2的边权需要乘上c
int sx, sy, ex, ey, B, m, n;  // (sx, sy)为起点, (ex, ey)为终点，B为限制条件，m为边类型数目，n为站点数

void add(int a, int b, LL c1, LL c2) {  // c1为边权，c2为限制条件
    e[idx] = b, w1[idx] = c1, w2[idx] = c2, ne[idx] = h[a], h[a] = idx++;
}

// 计算id1和id2之间的距离
LL getdis(int id1, int id2) {
    int x1 = point[id1].x, x2 = point[id2].x, y1 = point[id1].y, y2 = point[id2].y;
    return (LL)ceil(sqrt((x2 - x1) * 1ll * (x2 - x1) + (y2 - y1) * 1ll * (y2 - y1)));
}

// 有条件限制的dijkstra算法
LL dijkstra() {
    priority_queue q;  // 定义一个按照距离从小到大排序的优先队列
    memset(dis, 0x3f, sizeof dis);  // 距离初始化
    q.push({n, 0, 0});  // 把起点放入队列
    dis[n][0] = 0;  // 记录源点的距离

    while (q.size()) {
        auto t = q.top();
        q.pop();
        
        LL ver = t.point, distance = t.distance, strict = t.strict;  // 点、距离、限制条件
        if (st[ver][strict]) continue;  // 如果走过
        st[ver][strict] = 1;
        
        for (int i = h[ver]; ~i; i = ne[i]) {   // 遍历ver的所有出边
            int j = e[i];
            if (strict + w2[i] > B) continue;  // 如果超过限制条件，跳过
            if (dis[j][strict + w2[i]] > distance + w1[i]) {  // 如果能够更新
                dis[j][strict + w2[i]] = distance + w1[i];  // 更新
                q.push({j, dis[j][strict + w2[i]], strict + w2[i]});  // 放入优先队列
            }
        }
    }

    LL res = INF;  // 记录到终点点的最小距离
    for (int i = 0; i <= B; ++i) res = min(res, dis[n + 1][i]);  // 遍历每一个限制条件
    return res == INF? -1: res;
}

int main() {
    memset(h, -1, sizeof h);
    cin >> sx >> sy >> ex >> ey >> B >> C[0] >> m;  // 读入起点、终点、限制条件、初始边类型参数、边类型数目
    for (int i = 1; i <= m; ++i) scanf("%lld", &C[i]);  // 读入不同类型的边参数
    cin >> n;
    vector path;  // 记录所有的连边
    for (int i = 0, t; i < n; ++i) {
        scanf("%d%d", &point[i].x, &point[i].y);
        point[i].id = i;
        cin >> t;
        for (int j = 1, obj, c; j <= t; ++j) {
            scanf("%d%d", &obj, &c);
            path.push_back({i, obj, c});
        }
    }
    
    // 记录起点和终点
    point[n].x = sx, point[n].y = sy, point[n + 1].x = ex, point[n + 1].y = ey;
    point[n].id = n, point[n + 1].id = n + 1;
    
    // 起点和终点能够连到所有的站点
    for (auto p: path) {
        add(p.id1, p.id2, C[p.c] * (LL)getdis(p.id1, p.id2), (LL)getdis(p.id1, p.id2));
        add(p.id2, p.id1, C[p.c] * (LL)getdis(p.id1, p.id2), (LL)getdis(p.id1, p.id2));
    }
    for (int i = 0; i < n; ++i) {
        add(n, i, C[0] * (LL)getdis(n, i), (LL)getdis(n, i));
        add(i, n, C[0] * (LL)getdis(n, i), (LL)getdis(n, i));
        add(n + 1, i, C[0] * (LL)getdis(n + 1, i), (LL)getdis(n + 1, i));
        add(i, n + 1, C[0] * (LL)getdis(n + 1, i), (LL)getdis(n + 1, i));
    }
    add(n, n + 1, C[0] * (LL)getdis(n, n + 1), (LL)getdis(n, n + 1));
    add(n + 1, n, C[0] * (LL)getdis(n, n + 1), (LL)getdis(n, n + 1));
        
    // 计算有条件的dijkstra算法
    cout << dijkstra();
    return 0;
}

2.5 bellman_ford求最短路 (O(nm)):可以处理最多经过k条边的题目，可以处理负权边，但因为时间复杂度较高，一般被spfa替代

#include 

using namespace std;

int const N = 510, M = 10010, INF = 0x3f3f3f3f;
struct EDGE {
    int a, b, c;
}edge[M];
int n, m, k, dis[N], backup[N];

// bellman-ford求有边数限制的最短路
void bellman_ford() {
    memset(dis, 0x3f, sizeof dis);  // 初始化为无穷
    dis[1] = 0;  // 源点初始化
    for (int i = 1; i <= k; ++i) {  // 每次循环起码得到一个正确的dis
        memcpy(backup, dis, sizeof dis);  // 备份，防止拿本回合更新过的更新其他边
        for (int j = 1; j <= m; ++j) {  // 枚举所有的边
            int a = edge[j].a, b = edge[j].b, c = edge[j].c;  
            dis[b] = min(backup[a] + c, dis[b]);  // 更新
        }
    }
    if (dis[n] > INF / 2) cout << "impossible";  // 防止出现负权边情况
    else cout << dis[n];
}

int main() {
    cin >> n >> m >> k;
    for (int i = 1, a, b, c; i <= m; ++i) {
        scanf("%d %d %d", &a, &b, &c); 
        edge[i] = {a, b, c};  // 读入单向边
    }
    bellman_ford();  
    return 0;
}

2.6 spfa求最短路: O(km),最坏复杂度可以到O(nm),可被网格图卡，可以处理负权边

#include 

using namespace std;

int const N = 1e5 + 10, INF = 0x3f3f3f3f;
int e[N], ne[N], w[N], h[N], idx, m, n, dis[N], st[N];  // dis[i]标识i点到源点的最短距离，st[i]=1表示i点在队列里

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

// spfa求最短路
void spfa() {
    memset(dis, 0x3f, sizeof dis);  // 初始化最短路
    queue q;  // 建立新队列
    dis[1] = 0;  // 源点距离为0
    st[1] = 1;  // 标识源点在队列里了
    q.push(1);  // 源点入队
    
    while (q.size()) {
        auto t = q.front();  
        q.pop();  // 队首元素出队
        st[t] = 0;  // 记录出队
        
        for (int i = h[t]; ~i; i = ne[i]) {  // 遍历所有邻接点
            int j = e[i];
            if (dis[j] > dis[t] + w[i]) {  // 如果距离能够更新
                dis[j] = dis[t] + w[i];  // 更新距离
                if (!st[j]) {  // 如果j点不在队列里
                    q.push(j);  // 入队
                    st[j] = 1;  // 记录
                }
            }
        }
    }
    
    if (dis[n] == INF) cout << "impossible";
    else cout << dis[n];
}

int main() {
    memset(h, -1, sizeof h);
    cin >> n >> m;
    for (int i = 1, a, b, c; i <= m; ++i) {
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);  // 读入单向边
    }
    spfa();
    return 0;
}

2.7 spfa求最长路

// 与求最短路不同的是:
// 1. 初始化：memset(dis, 0xc0, sizeof dis);
// 2. 更新条件变成dis[j] < dis[t] + w[i]
#include 

using namespace std;

int const N = 1510, M = 5e4 + 10, INF = 0xc0c0c0c0;
int e[M], ne[M], w[M], h[N], idx, m, n, dis[N], st[N];  // dis[i]标识i点到源点的最短距离，st[i]=1表示i点在队列里

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

// spfa求最长路
void spfa() {
    memset(dis, 0xc0, sizeof dis);  // 初始化最长路
    queue q;  // 建立新队列
    dis[1] = 0;  // 源点距离为0
    st[1] = 1;  // 标识源点在队列里了
    q.push(1);  // 源点入队
    
    while (q.size()) {
        auto t = q.front();  
        q.pop();  // 队首元素出队
        st[t] = 0;  // 记录出队
        
        for (int i = h[t]; ~i; i = ne[i]) {  // 遍历所有邻接点
            int j = e[i];
            if (dis[j] < dis[t] + w[i]) {  // 如果距离能够更新
                dis[j] = dis[t] + w[i];  // 更新距离
                if (!st[j]) {  // 如果j点不在队列里
                    q.push(j);  // 入队
                    st[j] = 1;  // 记录
                }
            }
        }
    }
    
    cout << (dis[n] == INF? -1: dis[n]);
}

int main() {
    memset(h, -1, sizeof h);
    cin >> n >> m;
    for (int i = 1, a, b, c; i <= m; ++i) {
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);  // 读入单向边
    }
    spfa();
    return 0;
}

2.8 bfs最短路模型求最短路: O(m + n): 只能处理边权为1的情况

#include 

using namespace std;

int const N = 1e3 + 10;
int a[N][N], st[N][N], n;
int pre[N * N];
queue >q;
vector > path;
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};

void bfs(pair start) {
    q.push(start);
    st[start.first][start.second] = 1;
    
    while (q.size()) {
        auto t = q.front();
        q.pop();
        
        for (int i = 0; i < 4; ++i) {
            int x = t.first + dx[i], y = t.second + dy[i];
            if (x < 0 || x > n - 1 || y < 0 || y > n - 1) continue;
            if (st[x][y] || a[x][y] == 1) continue;
            
            pre[x * n + y] = t.first * n + t.second;
            if (x == n - 1 && y == n - 1) return;
            
            st[x][y] = 1;
            q.push({x, y});
        }
    }
}

pair get_pos(int x) {
    pair res;
    res.first = x / n;
    res.second = x % n;
    return res;
}

int main() {
    cin >> n;
    for (int i = 0; i < n; ++i) 
        for (int j = 0; j < n; ++j)
            cin >> a[i][j];
    
    bfs({0, 0});
    int cur = (n - 1) * n + n - 1;
    while (1) {
        path.push_back(get_pos(cur));
        cur = pre[cur];
        if (cur == 0) break;
    }
    path.push_back({0, 0});
    reverse(path.begin(), path.end());
    for (auto p: path) 
        cout << p.first << " " << p.second << endl;
    return 0;
}

2.9 拓扑排序模型求最短路: O(m+n):必须为DAG

#include

using namespace std;

int const N = 2e3 + 10, M = 2e6 + 10;
int n, m;
int e[M], ne[M], h[N], w[M], idx;
int din[N], st[N], dis[N];
vector ans;

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

// 拓扑排序
void topsort() {
    queue q;
    for (int i = 1; i <= n + m; ++i) if (!din[i]) q.push(i);

    while (q.size()) {
        auto t = q.front();
        q.pop();
        ans.push_back(t);

        for (int i = h[t]; ~i; i = ne[i]) {
            int j = e[i];
            din[j]--;
            if (!din[j]) q.push(j);
        }
    }
}

int main()
{
    memset(h, -1, sizeof h);
    cin >> n >> m;
    for (int i = 1; i <= m; ++i) {
        // 建图（加入虚节点，平方->线性）
        memset(st, 0, sizeof st);
        int cnt, start = n, end = 1, ver = n + i;  // start记录最小的点，end记录最大的点，ver记录虚拟节点
        cin >> cnt;
        for (int i = 0; i < cnt; ++i) {
            int t;
            cin >> t;
            st[t] = 1;
            start = min(start, t);
            end = max(end, t);
        }

        // 把a->b的边拆成a->ver和ver->b
        for (int j = start; j <= end; ++j) {
            if (st[j]) add(ver, j, 1), din[j]++;
            else add(j, ver, 0), din[ver]++;
        }
    }

    // 拓扑排序得到更新的顺序
    topsort();

    // dp求最大值
    for (int i = 1; i <= n; ++i) dis[i] = 1;
    for (int i = 0; i < ans.size(); ++i) {
        int k = ans[i];
        for (int j = h[k]; ~j; j = ne[j]) {
            int t = e[j];
            dis[t] = max(dis[t], dis[k] + w[j]);
        }
    }

    int res = 0;
    for (int i = 1; i <= n; ++i) res = max(res, dis[i]);
    cout << res << endl;
    return 0;
}

2.10 floyd最短路问题 O(n^3)

#include 

using namespace std;

int const N = 210, INF = 0x3f3f3f3f;
int mp[N][N], n, m, k;

// floyd求最短路
void floyd() {
    for (int k = 1; k <= n; ++k)  // 枚举中间点
        for (int i = 1; i <= n; ++i)  // 枚举起点
            for (int j = 1; j <= n; ++j)  // 枚举终点
                mp[i][j] = min(mp[i][j], mp[i][k] + mp[k][j]);  // 更新i到j的距离
}

int main() {
    cin >> n >> m >> k;  // 点、边、询问次数
    
    // 初始化距离：初始化为正无穷
    for (int i = 1; i <= n; ++i) 
        for (int j = 1; j <= n; ++j) 
            mp[i][j] = (i == j? 0: INF);  
            
    // 读入边
    for (int i = 1, a, b, c; i <= m; ++i) {
        scanf("%d%d%d", &a, &b, &c);
        mp[a][b] = min(mp[a][b], c);
    }
    
    // 求最短路
    floyd();
    
    // 询问
    for (int i = 1, a, b; i <= k; ++i) {
        scanf("%d%d", &a, &b);
        if (mp[a][b] > INF / 2) cout << "impossible\n";  // 防止负权边，所有用INF/2
        else cout << mp[a][b] << endl;  // 打印
    }
    
    return 0;
}

3. 典型例题

3.1 有等级差值的限制的最短路

acwing903. 昂贵的聘礼
题意：
年轻的探险家来到了一个印第安部落里。在那里他和酋长的女儿相爱了，于是便向酋长去求亲。酋长要他用10000个金币作为聘礼才答应把女儿嫁给他。探险家拿不出这么多金币，便请求酋长降低要求。酋长说：”嗯，如果你能够替我弄到大祭司的皮袄，我可以只要8000金币。如果你能够弄来他的水晶球，那么只要5000金币就行了。”探险家就跑到大祭司那里，向他要求皮袄或水晶球，大祭司要他用金币来换，或者替他弄来其他的东西，他可以降低价格。探险家于是又跑到其他地方，其他人也提出了类似的要求，或者直接用金币换，或者找到其他东西就可以降低价格。不过探险家没必要用多样东西去换一样东西，因为不会得到更低的价格。探险家现在很需要你的帮忙，让他用最少的金币娶到自己的心上人。另外他要告诉你的是，在这个部落里，等级观念十分森严。地位差距超过一定限制的两个人之间不会进行任何形式的直接接触，包括交易。他是一个外来人，所以可以不受这些限制。
但是如果他和某个地位较低的人进行了交易，地位较高的的人不会再和他交易，他们认为这样等于是间接接触，反过来也一样。因此你需要在考虑所有的情况以后给他提供一个最好的方案。为了方便起见，我们把所有的物品从1开始进行编号，酋长的允诺也看作一个物品，并且编号总是1。每个物品都有对应的价格P，主人的地位等级L，以及一系列的替代品Ti和该替代品所对应的”优惠”Vi。如果两人地位等级差距超过了M，就不能”间接交易”。你必须根据这些数据来计算出探险家最少需要多少金币才能娶到酋长的女儿。
1≤N≤100,1≤P≤10000,1≤L,M≤N,0≤X 题解： 本题要求1~n的路径上有等级差值的限制的最短路。 建立虚拟源点，然后做dijkstra。为了解决等级限制，就暴力去枚举能够使用的等级区间，dijkstra要满足等级区间限制才能进行转移。
代码：

#include 

using namespace std;

const int N = 110, INF = 0x3f3f3f3f;

int n, m;
int w[N][N], level[N];
int dist[N];
bool st[N];

// dijkstra时要有等级的限制
int dijkstra(int down, int up) {
    memset(dist, 0x3f, sizeof dist);
    memset(st, 0, sizeof st);

    dist[0] = 0;
    for (int i = 1; i <= n + 1; i ++ ) {
        int t = -1;
        for (int j = 0; j <= n; j ++ )
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                 t = j;

        st[t] = true;
        for (int j = 1; j <= n; j ++ )
            if (level[j] >= down && level[j] <= up)  // 满足上下界才能转移
                dist[j] = min(dist[j], dist[t] + w[t][j]);
    }

    return dist[1];
}

int main() {
    cin >> m >> n;

    memset(w, 0x3f, sizeof w);
    for (int i = 1; i <= n; i ++ ) w[i][i] = 0;

    for (int i = 1; i <= n; i ++ ) {
        int price, cnt;
        cin >> price >> level[i] >> cnt;
        w[0][i] = min(price, w[0][i]);
        while (cnt -- ) {
            int id, cost;
            cin >> id >> cost;
            w[id][i] = min(w[id][i], cost);
        }
    }

    int res = INF;
    // 枚举和1号点相关的等级区间
    for (int i = level[1] - m; i <= level[1]; i ++ ) res = min(res, dijkstra(i, i + m));  

    cout << res << endl;

    return 0;
}

3.2 有枚举顺序的最短路

acwing1135.新年好
题意： 重庆城里有 n 个车站，m 条 双向 公路连接其中的某些车站。每两个车站最多用一条公路连接，从任何一个车站出发都可以经过一条或者多条公路到达其他车站，但不同的路径需要花费的时间可能不同。在一条路径上花费的时间等于路径上所有公路需要的时间之和。佳佳的家在车站 1，他有五个亲戚，分别住在车站 a,b,c,d,e。过年了，他需要从自己的家出发，拜访每个亲戚（顺序任意），给他们送去节日的祝福。怎样走，才需要最少的时间？
\(1≤n≤50000,1≤m≤10^5,1
题解： 本题要求找到一条路径，该路径能够穿过给定的有限个点，找到这样一条最短路。 分别以5个点为起点，各做dijkstra，这样就能够得到这5个点到其他店的最短路。然后dfs枚举拜访的顺序即可
代码：

#include 

using namespace std;

typedef pair PII;
int const N = 2e5 + 10;
int e[N], ne[N], w[N], h[N], idx;
int n, m;
int dis[6][N];
int st[6];
int source[6];
int q[N];

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

void dijkstra(int s, int dist[]) {
    memset(dist, 0x3f, N * 4);
    priority_queue, greater> heap;
    heap.push({0, s});
    dist[s] = 1;
    while (heap.size()) {
        auto t = heap.top();
        heap.pop();
        int distance = t.first, ver = t.second;
        for (int i = h[ver]; i != -1; i = ne[i]) {
            int j = e[i];
            if (dist[j] > distance + w[i]) {
                dist[j] = distance + w[i];
                heap.push({dist[j], j});
            }
        }
    }
}

int dfs(int u, int start, int distance) {
    if (u > 5) return distance;
    int res = 0x3f3f3f3f;
    for (int i = 1; i <= 5; ++i) {
        if (!st[i]) {
            st[i] = 1 ;
            res = min(res , dfs(u + 1, i, distance + dis[start][source[i]]));
            st[i] = 0;
        }
    }
    return res;
}

int main() {
    cin >> n >> m;
    source[0] = 1;
    for (int i = 1; i <= 5; ++i) cin >> source[i];
    memset(h, -1, sizeof h);
    for (int i = 1; i <= m; ++i) {
        int a, b, c;
        scanf("%d %d %d", &a, &b, &c);
        add(a, b, c), add(b, a, c);
    }
    for (int i = 0; i <= 5; ++i)
        dijkstra(source[i], dis[i]);

    printf("%d\n", dfs(1, 0, 0));
    return 0;
}

3.3 找出第k+1大的边权值

acwing340. 通信线路
题意： 在郊区有 N 座通信基站，P 条 双向 电缆，第 i 条电缆连接基站Ai和Bi。特别地，1 号基站是通信公司的总站，N 号基站位于一座农场中。现在，农场主希望对通信线路进行升级，其中升级第 i 条电缆需要花费Li。电话公司正在举行优惠活动。农产主可以指定一条从 1 号基站到 N 号基站的路径，并指定路径上不超过 K 条电缆，由电话公司免费提供升级服务。农场主只需要支付在该路径上剩余的电缆中，升级价格最贵的那条电缆的花费即可。求至少用多少钱可以完成升级。
题解： 找1~n上第k+1大的路径。 二分检查答案，然后每次把比答案大的边当成1，比答案小的边当成0，做dijkstra，check的条件就是dis[n]和k的关系。
代码：

#include
 
using namespace std;

int const N = 2e4 + 10;
int e[N], ne[N], w[N], idx, h[N];
int k, n, p;
int dis[N];
int st[N];

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

bool check(int bound) {
    memset(dis, 0x3f, sizeof dis);
    memset(st, 0, sizeof st);
    dis[1] = 0;
    deque q;
    q.push_front(1);
    while (q.size()) {
        auto t = q.front();
        q.pop_front();
        if (st[t]) continue;
        st[t] = 1;
        for (int i = h[t]; i != -1; i = ne[i]) {
            int j = e[i];
            int len = w[i] > bound;
            if (dis[j] > dis[t] + len) {
                dis[j] = dis[t] + len;
                if (len) q.push_back(j);
                else q.push_front(j);
            }
        }
    }
    return dis[n] <= k;
}
 
int main() {
    memset(h, -1, sizeof h);
    cin >> n >> p >> k;
    for (int i = 1; i <= p; ++i) {
        int a, b, c;
        scanf("%d %d %d", &a, &b, &c);
        add(a, b, c), add(b, a, c);
    }
    int l = 0, r = 1e6 + 1;
    while (l < r) {
        int mid = (l + r) >> 1;
        if (check(mid)) r = mid;
        else l = mid + 1;
    }
    if (l == 1e6 + 1) cout << -1 << endl;
    else cout << l << endl;
    return 0;
}

3.4 存在有向边和无向边的图找最短路

acwing342. 道路与航线
题意： 农夫约翰正在一个新的销售区域对他的牛奶销售方案进行调查。他想把牛奶送到T个城镇，编号为1~T。这些城镇之间通过R条道路 (编号为1到R) 和P条航线 (编号为1到P) 连接。每条道路 i 或者航线 i 连接城镇Ai到Bi，花费为Ci。对于道路，0≤Ci≤10,000;然而航线的花费很神奇，花费Ci可能是负数(−10,000≤Ci≤10,000)。道路是双向的，可以从Ai到Bi，也可以从Bi到Ai，花费都是Ci。然而航线与之不同，只可以从Ai到Bi。事实上，由于最近恐怖主义太嚣张，为了社会和谐，出台了一些政策：保证如果有一条航线可以从Ai到Bi，那么保证不可能通过一些道路和航线从Bi回到Ai。由于约翰的奶牛世界公认十分给力，他需要运送奶牛到每一个城镇。他想找到从发送中心城镇S把奶牛送到每个城镇的最便宜的方案。\(1≤T≤25000,1≤R,P≤50000,1≤Ai,Bi,S≤T\)
题解： 本题要在一张既有有向边又有无向边的图上求出每个点到源点的最短距离，保证有向边不会形成有向环。 先把无向边建的图分成很多连通块，缩成超级点。再加上有向边后，整张图就变成一张dag。然后拓扑排序求最短路，当处理超级点时，用堆优化版dijkstra处理，dijkstra需要添加上一些特判的逻辑，具体见代码。
代码：

#include
 
using namespace std;

typedef pair PII;
int const N = 3e4 + 10, M = 2e5 + 10;
int e[M], ne[M], w[M], idx, h[M];
int t, r, p, source;
int id[N];
vector block[N];
int bcnt;
int st[N];
int dis[N];
queue q;
int din[N];

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

// 按照连通块缩点
void dfs(int u, int cnt) {
    id[u] = cnt;
    block[cnt].push_back(u);
    for (int i = h[u]; i != -1; i = ne[i]) {
        int j = e[i];
        if (!id[j]) dfs(j, cnt);
    }
}

// 堆优化版dijkstra算法求连通块内的最短路
void dijkstra(int bid) { 
    priority_queue, greater >heap;
    for (auto b: block[bid]) heap.push({dis[b], b});
    while (heap.size()) {
        auto t = heap.top();
        heap.pop();
        int distance = t.first, ver = t.second;
        if (st[ver]) continue;
        st[ver] = 1;
        for (int i = h[ver]; i != -1; i = ne[i]) {
            int j = e[i];
            if (dis[j] > distance + w[i])
            {
                dis[j] = distance + w[i];
                if (id[ver] == id[j]) heap.push({dis[j], j});  // 如果是一个超级点内才能更新
            }
            if (id[ver] != id[j])  // 不在一个超级点内，那么需要按照拓扑排序逻辑更新
            {
                din[id[j]]--;
                if (!din[id[j]]) q.push(id[j]);
            }
        }
    }
}

// 拓扑排序求最短路
void top_sort() {
    for (int i = 1; i <= bcnt; ++i)
        if (!din[i]) q.push(i);
    memset(dis, 0x3f, sizeof dis);
    memset(st, 0, sizeof st);
    dis[source] = 0;
    while (q.size()) {
        auto t = q.front();
        q.pop();
        dijkstra(t);
    }
}
 
int main() {
    memset(h, -1, sizeof h);
    cin >> t >> r >> p >> source;
    for (int i = 1; i <= r; ++i) {  // 读入无向边
        int a, b, c;
        scanf("%d %d %d", &a, &b, &c);
        add(a, b, c);
        add(b, a, c);
    }
    for (int i = 1; i <= t; ++i) {  // 把所有点按照连通块划分为超级点
        if (!id[i]) dfs(i, ++bcnt);
    }
    for (int i = 1; i <= p; ++i) {  // 读入有向边
        int a, b, c;
        scanf("%d %d %d", &a, &b, &c);
        add(a, b, c);
        din[id[b]]++;
    }
    top_sort();  // 拓扑排序求最短路
    for (int i = 1; i <= t; ++i) {  // 判断是否有最短路
        if (dis[i] > 0x3f3f3f3f / 2) cout << "NO PATH\n";
        else cout << dis[i] << endl;
    }
    return 0;
}

acwing341. 最优贸易
题意： C国有 n 个大城市和 m 条道路，每条道路连接这 n 个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这 m 条道路中有一部分为单向通行的道路，一部分为双向通行的道路，双向通行的道路在统计条数时也计为1条。C国幅员辽阔，各地的资源分布情况各不相同，这就导致了同一种商品在不同城市的价格不一定相同。但是，同一种商品在同一个城市的买入价和卖出价始终是相同的。商人阿龙来到C国旅游。当他得知“同一种商品在不同城市的价格可能会不同”这一信息之后，便决定在旅游的同时，利用商品在不同城市中的差价赚一点旅费。设C国 n 个城市的标号从 1~n，阿龙决定从1号城市出发，并最终在 n 号城市结束自己的旅行。在旅游的过程中，任何城市可以被重复经过多次，但不要求经过所有 n 个城市。阿龙通过这样的贸易方式赚取旅费：他会选择一个经过的城市买入他最喜欢的商品——水晶球，并在之后经过的另一个城市卖出这个水晶球，用赚取的差价当做旅费。因为阿龙主要是来C国旅游，他决定这个贸易只进行最多一次，当然，在赚不到差价的情况下他就无需进行贸易。现在给出 n 个城市的水晶球价格，m 条道路的信息（每条道路所连接的两个城市的编号以及该条道路的通行情况）。请你告诉阿龙，他最多能赚取多少旅费。\(1≤n≤100000,1≤m≤500000,1≤各城市水晶球价格≤100\)
题解： 本题要在一张既有有向边又有无向边的图上，找出两个点i和j(i和j均在1~n的路径上)，使得\(w[j]-w[i]\)最大，其中i在的前面出现，有向边可能形成有向环。 本题要找1 ~ n上最大的点和最小的点。考虑dp求解，维护数组f1[i]表示i点开始到n点的最大价值，然后去枚举i为买的点，答案即为max{val[i]-f1[i]}。但是本题可能存在环，因此考虑tarjan算法缩点变成dag(有向边的环缩点，无向边的联通块也会缩点)。本题的难点在于要求当前的点i必须是从1开始，到n结束。从1开始好处理，tarjan算法的时候只做1为起点的tarjan，这样求出来的都是从1开始的。而到n结束就必须维护一个数组f2[i]表示i是否能够到n点,f2[i]为1表示i能够到n点，为0表示不能到n点，每次都必须更新f2。维护数组f1[i]表示i点开始到n点的最大价值，当且仅当f2[i]=1才能转移，f1[i]=max[max{f1[u]}, val[i]]
代码：

#include

using namespace std;

typedef pair PII;

int const N = 2e5 + 10, M = 2e6 + 10;
// dfn记录每个点的时间戳,low记录每个点的回溯值，scc[i]=x表示i在标号为x的强连通分量里，stk维护一个栈,sccnum记录强连通分量的个数
int dfn[N], low[N], scc[N], stk[N], sccnum, top, timestamp;  
int h1[N], e[M], ne[M], idx, h2[N], w[N];
int n, m;
int f1[N], f2[N]; //f1[i]表示i点开始到n点的最大价值, f2[i]为1表示i能够到n点，为0表示不能到n点
PII scc_count[N];  // first为max，second为min

// a->b有一条边
void add(int a, int b, int h[])
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}   

// tarjan算法求强连通分量
void tarjan(int root, int h[])
{
    if (dfn[root]) return;  // 时间戳为0，返回
    dfn[root] = low[root] = ++timestamp;  // 记录当前点的时间戳和回溯值，初始化二者相同，而后dfn[root]>=low[root]
    stk[++top] = root;  // 把根放入栈内
    for (int i = h[root]; i != -1; i = ne[i])  // 遍历每一个与根节点相邻的点
    {
        int j = e[i];  // 与i相邻的点为j
        if (!dfn[j])  // j点没有访问过
        {
            tarjan(j, h);  // 继续dfs，得到所有以j点为根的子树内所有的low和dfn
            low[root] = min(low[root], low[j]);  // 根的low是其子树中low最小的那个
        }
        else if (!scc[j])  // 如果j这个点还在栈内(在栈内的话不属于任何一个scc),同时一个栈内的点在一个scc内
        {
            low[root] = min(low[root], dfn[j]);  // low代表所能到达的最小的时间戳
        }
    }
    
    // 如果root的后代不能找到更浅的节点(更小的时间戳)
    if (low[root] == dfn[root])  // 只有某个强连通分量的根节点的low和dfn才会相同
    {
        sccnum++;
        scc_count[sccnum].first = -1;  // 计算最大值和最小值
        scc_count[sccnum].second = 1e9;
        while (1)  // 出栈直到等于root
        {
            int x = stk[top--];
            if (x == n) f2[sccnum] = 1;
            scc[x] = sccnum;
            scc_count[sccnum].first = max(scc_count[sccnum].first, w[x]);
            scc_count[sccnum].second = min(scc_count[sccnum].second, w[x]);
            if (x == root) break;
        }
    }
}

int main()
{
    cin >> n >> m;
    memset(h1, -1, sizeof h1);
    memset(h2, -1, sizeof h2);
    memset(f1, -1, sizeof f1);
    
    for (int i = 1; i <= n; ++i) scanf("%d", &w[i]);
    for (int i = 1, a, b, t; i <= m; ++i)
    {
        scanf("%d %d %d", &a, &b, &t);
        add(a, b, h1);
        if (t == 2) add(b, a, h1);
    }

    // tarjan求scc
    tarjan(1, h1);  // 这样保证后面缩点的所有点都是从1开始
    
    // 缩点
    for (int i = 1; i <= n; ++i)
        for (int j = h1[i]; j != -1; j = ne[j])
        {
            int k = e[j];
            if (scc[i] != scc[k] && scc[i] && scc[k]) add(scc[i], scc[k], h2);
        }
    
    // 反拓扑序做dp
    int ans = 0;
    for (int i = 1; i <= sccnum; ++i) {  
        int maxv = -1;
        for (int j = h2[i]; ~j; j = ne[j]) {
            int k = e[j];
            f2[i] |= f2[k];  // 更新i是否能够到达终点的情况
            if (f2[k]) maxv = max(maxv, f1[k]);  // 更新能够到达终点的最大值
        }
        if (f2[i]) {  // 只要f2为1才更新
            f1[i] = max(scc_count[i].first, maxv);
            ans = max(ans, f1[i] - scc_count[i].second);
        }
    }

    cout << ans;

    return 0;
}

3.5 有条件限制的最短路

题意： 瑞恩被关在N*M的迷宫里。南北或东西方向相邻的 2 个单元之间可能互通，也可能有一扇锁着的门，或者是一堵不可逾越的墙。注意： 门可以从两个方向穿过，即可以看成一条无向边。迷宫中有一些单元存放着钥匙，同一个单元可能存放 多把钥匙，并且所有的门被分成 P 类，打开同一类的门的钥匙相同，不同类门的钥匙不同。瑞恩被关押在 (N,M) 单元里。从(1, 1)进入迷宫，从一个单元移动到另一个相邻单元的时间为 1，拿取所在单元的钥匙的时间以及用钥匙开门的时间可忽略不计。问最少多少时间可以把瑞恩拯救出来。
\(|Xi1−Xi2|+|Yi1−Yi2|=1,0≤Gi≤P,1≤Qi≤P,1≤N,M,P≤10,1≤k≤150\)
题解： 本题是有条件限制的最短路，限制的条件为钥匙。因此可以专门拿出一维来做限制条件，然后做最短路时要满足限制条件才能转移。
因此本题分以下4个步骤：
1.读边：如果是门的话记录下
2.建图：
3.读钥匙
4.做双端bfs
代码：

#include

using namespace std;

typedef pair PII;
int const N = 4e2 + 10;
int e[N], ne[N], idx, w[N], h[N];
int cnt;
int n, m, p, k, s;
int dis[110][1 << 10], st[110][1 << 10];
int g[15][15], key[110];
set exist;

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

// 建图：找四周可以走的点
void build()
{
    int dx[4] = {0, 1, 0, -1}, dy[4] = {1, 0, -1, 0};
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= m; ++j)
        {
            for (int u = 0; u < 4; ++u)
            {
                int x = i + dx[u], y = j + dy[u];
                if (x <= 0 || x > n || y <= 0 || y > m) continue;
                if (exist.count({g[i][j], g[x][y]})) continue;
                add(g[i][j], g[x][y], 0);
            }
        }
}

int bfs()
{
    memset(dis, 0x3f, sizeof dis);
    dis[1][0] = 0;

    deque q;
    q.push_back({1, 0});  // 第一维为点，第二维维拥有的钥匙

    while (q.size())
    {
        PII t = q.front();
        q.pop_front();

        if (st[t.first][t.second]) continue;
        st[t.first][t.second] = true;

        if (t.first == n * m) return dis[t.first][t.second];

        // 在本地不动，更新钥匙情况
        if (key[t.first])
        {
            int state = t.second | key[t.first];  // 更新手中的钥匙状态
            if (dis[t.first][state] > dis[t.first][t.second])
            {
                dis[t.first][state] = dis[t.first][t.second];
                q.push_front({t.first, state});
            }
        }

        // 向四周走
        for (int i = h[t.first]; ~i; i = ne[i])
        {
            int j = e[i];
            if (w[i] && !(t.second >> w[i] - 1 & 1)) continue;   // 有门并且没有钥匙
            if (dis[j][t.second] > dis[t.first][t.second] + 1)
            {
                dis[j][t.second] = dis[t.first][t.second] + 1;
                q.push_back({j, t.second});
            }
        }
    }

    return -1;
}

int main()
{
    memset(h, -1, sizeof h);

    // 给每个坐标标号
    cin >> n >> m >> p;
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= m; ++j)
            g[i][j] = ++cnt;
    
    // 读边
    cin >> k;
    for (int i = 0; i < k; ++i)
    {
        int x1, y1, x2, y2, type;
        scanf("%d %d %d %d %d", &x1, &y1, &x2, &y2, &type);
        int a = g[x1][y1], b = g[x2][y2];
        exist.insert({a, b}), exist.insert({b, a});
        if (type)
        {
            add(a, b, type);  // 边的权值为钥匙的种类
            add(b, a, type);
        }
    }

    // 建图
    build();

    // 读钥匙
    cin >> s;
    for (int i = 0; i < s; ++i)
    {
        int x, y, type;
        scanf("%d %d %d", &x, &y, &type);
        key[g[x][y]] |= 1 << type - 1;  // 记录每个点的钥匙
    }

    // 做双端bfs
    cout << bfs() << endl;

    return 0;
}

3.6 最短路计数模型

AcWing 1134. 最短路计数
题意： 给出一个 N 个顶点 M 条边的无向无权图，顶点编号为 1 到 N。问从顶点 1 开始，到其他每个点的最短路有几条。
题解： 对于点j，其前缀点有u1，u2，u3，即方案数cnt[j],那么:
if (dis[j] > dis[u] + 1) {
dis[j] = dis[u] + 1;
cnt[j] = cnt[ver];
}
else if (dis[j] == distance + 1) cnt[j] += cnt[u];
初始时方案数为1
同时，bfs和dijkstra算法求出的点的顺序是拓扑序，可以直接处理这类问题
而spfa算法出点的顺序不一定是拓扑序，不能直接处理这个问题，但是可以间接处理这个问题；
比如存在负权边情况下，可以先使用spfa求出拓扑关系（即求出所有dis[j]=dis[u]+g[u][j]）那么可以知道
u->j就是一个拓扑序，一旦知道了拓扑序，就可以bfs求出方案数了
代码：

#include

using namespace std;

typedef pair PII;

int n, m;
int const N = 4e5 + 10, MOD = 1e5 + 3, INF = 0x3f3f3f3f;
int e[N], ne[N], idx, h[N];
int dis[N], cnt[N], st[N];

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

// 跑最短路
void dijkstra() {
    memset(dis, 0x3f, sizeof dis);
    memset(st, 0, sizeof st);

    priority_queue, greater > q;
    q.push({0, 1});
    dis[1] = 0;
    cnt[1] = 1;

    while (q.size()) {
        auto t = q.top();
        q.pop();
        int ver = t.second, distance = t.first;
        if (st[ver]) continue;
        st[ver] = 1;
        
        for (int i = h[ver]; ~i; i = ne[i]) {
            int j = e[i];

            // 更新最短路和方案数
            if (dis[j] > distance + 1) {
                dis[j] = distance + 1;
                cnt[j] = cnt[ver];
                q.push({dis[j], j});
            }
            else if (dis[j] == distance + 1) cnt[j] = (cnt[j] + cnt[ver]) % MOD;
        }
    }
}

int main() {
    memset(h, -1, sizeof h);

    // 建图
    cin >> n >> m;
    for (int i = 0; i < m; ++i) {
        int a, b;
        scanf("%d %d", &a, &b);
        add(a, b), add(b, a);
    }

    // 跑最短路
    dijkstra();

    // 输出
    for (int i = 1; i <= n; ++i) printf("%d\n", dis[i] == INF? 0: cnt[i]);

    return 0;
}

3.7 次短路模型

acwing383. 观光
题意： 给定一张n个点m条的有向图，求出有向图中最短路的数目+次短路的数目。(本题要求次短路长度为最短路长度+1)
题解：
本题在求最短路方案的基础上要求次短路
求解次短路可以维护一个dis[j][1]表示到j点的次短路的距离，cnt[j][1]表示到j点次短路的方案
然后求的过程中把次短路当成一个新的节点求即可
次短路的会出现4个情况
if (dist[j][0] > distance + w[i])：能够更新最短路（那么自然次短路也会被更新）
else if (dist[j][0] == distance + w[i]) （不能够更新最短路，那么次短路不会被更新）
else if (dist[j][1] > distance + w[i])（不能更新最短路，但是能够更新次短路）
else if (dist[j][1] == distance + w[i]) （不能更新最短路，也不能更新次短路）
代码：

#include

using namespace std;

const int N = 1010, M = 20010;

struct Ver {
    int id, type, dist;
    bool operator> (const Ver &W) const {
        return dist > W.dist;
    }
};

int n, m, S, T;
int h[N], e[M], w[M], ne[M], idx;
int dist[N][2], cnt[N][2];
bool st[N][2];

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

int dijkstra()
{
    memset(st, 0, sizeof st);
    memset(dist, 0x3f, sizeof dist);
    memset(cnt, 0, sizeof cnt);

    dist[S][0] = 0, cnt[S][0] = 1;  // 第二维为1表示次短路，为0表示最短路
    priority_queue, greater> heap;
    heap.push({S, 0, 0});

    while (heap.size()) {
        Ver t = heap.top();
        heap.pop();

        int ver = t.id, type = t.type, distance = t.dist, count = cnt[ver][type];
        if (st[ver][type]) continue;
        st[ver][type] = true;

        for (int i = h[ver]; ~i; i = ne[i]) {
            int j = e[i];

            // 4种情况讨论
            if (dist[j][0] > distance + w[i]) {
                dist[j][1] = dist[j][0], cnt[j][1] = cnt[j][0];
                heap.push({j, 1, dist[j][1]});
                dist[j][0] = distance + w[i], cnt[j][0] = count;
                heap.push({j, 0, dist[j][0]});
            }
            else if (dist[j][0] == distance + w[i]) cnt[j][0] += count;
            else if (dist[j][1] > distance + w[i]) {
                dist[j][1] = distance + w[i], cnt[j][1] = count;
                heap.push({j, 1, dist[j][1]});
            }
            else if (dist[j][1] == distance + w[i]) cnt[j][1] += count;
        }
    }

    int res = cnt[T][0];
    if (dist[T][0] + 1 == dist[T][1]) res += cnt[T][1];  // 如果次短路和最短路仅差1

    return res;
}

int main() {
    int cases;
    scanf("%d", &cases);
    while (cases -- ) {
        scanf("%d%d", &n, &m);
        memset(h, -1, sizeof h);
        idx = 0;

        // 建图
        while (m -- ) {
            int a, b, c;
            scanf("%d%d%d", &a, &b, &c);
            add(a, b, c);
        }
        scanf("%d%d", &S, &T);
        // 计数最短路+次短路数目
        printf("%d\n", dijkstra());
    }

    return 0;
}

3.8 图论建图技巧

3.8.1 虚拟源点

acwing1137. 选择最佳线路
题意： 给定一张n个点m条边的有向图，每条边边权为t，有w个源点，一个汇点s，求出一条最短路能够从某个源点到达汇点。
\(1≤s≤n,0
题解： 多源问题添加一个虚拟节点作为源点，虚拟源点到其他源点的长度都为0，那么问题就变成单源汇问题。
代码：

#include

using namespace std;

typedef pair PII;

int const N = 1e3 + 10, M = 2e4 + 13, INF = 0x3f3f3f3f;
int e[M], ne[M], w[M], idx, h[M];
int n, m, t;
int dis[N], st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

int dijkstra()
{
    memset(dis, 0x3f, sizeof dis);
    memset(st, 0, sizeof st);
    priority_queue, greater > q;
    dis[n + 1] = 0;
    q.push({0, n + 1});
    while (q.size())
    {
        auto t = q.top();
        q.pop();
        int distance = t.first, ver = t.second;
        if (st[ver]) continue;
        st[ver] = 1;
        for (int i = h[ver]; ~i; i = ne[i])
        {
            int j = e[i];
            if (dis[j] > distance + w[i])
            {
                dis[j] = distance + w[i];
                q.push({dis[j], j});
            }
        }
    }
    return dis[t];
}

int main()
{
    while (scanf("%d %d %d", &n, &m, &t) != EOF)
    {
        memset(h, -1, sizeof h);
        idx = 0;

        for (int i = 0; i < m; ++i)
        {
            int a, b, c;
            scanf("%d %d %d", &a, &b, &c);
            add(a, b, c);
        }

        int s_num;
        scanf("%d", &s_num);
        for (int i = 0; i < s_num; ++i)  // 每个源点和虚拟源点连一条权值为0的边
        {
            int tmp;
            scanf("%d", &tmp);
            add(n + 1, tmp, 0);
        }

        int t = dijkstra();
        if (t == INF) printf("-1\n");
        else printf("%d\n", t);
    }
    return 0;
}

3.8.2 二分图建图优化建图

acwing456车站分级
题意： 一条单向的铁路线上，依次有编号为1, 2, …, n 的n个火车站。每个火车站都有一个级别，最低为1级。现有若干趟车次在这条线路上行驶，每一趟都满足如下要求：如果这趟车次停靠了火车站x，则始发站、终点站之间所有级别大于等于火车站x的都必须停靠。（注意：起始站和终点站自然也算作事先已知需要停靠的站点）
例如，下表是5趟车次的运行情况。
其中，前4趟车次均满足要求，而第5趟车次由于停靠了3号火车站（2级）却未停靠途经的6号火车站（亦为2级）而不满足要求。

现有m趟车次的运行情况（全部满足要求），试推算这n个火车站至少分为几个不同的级别。1≤n,m≤1000
题解： 很明显，不停靠的站点的优先级一定比停靠的站点的优先级要小，因此不停靠的站点的优先级最小为1，且停靠的站点的优先级>=不停靠的站点的优先级+1，则本题可以转换为一个差分约束问题，且边权大于等于0。(这里不需要tarjan判断是否有正环，因为明确了有解，不可能出现正环，所以直接拓扑排序求拓扑序(tarjan的目的也是缩点完求拓扑序))。本题的另一个难点在于建图，如果直接把不停靠的站点向停靠的站点连一条边，那么建图的复杂度为O(mn^2^)。对于一个二分图，左边的每个点都需要向右边每个点连一条边的建图模型来说，可以设置一个虚拟节点，然后使得左边每个点连向虚拟节点，虚拟节点再向右边每个点连边。这样就把O(n ^ 2)优化到O(n)。

代码：

#include

using namespace std;

int const N = 2e3 + 10, M = 2e6 + 10;
int n, m;
int e[M], ne[M], h[N], w[M], idx;
int din[N], st[N], dis[N];
vector ans;

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

// 拓扑排序
void topsort()
{
    queue q;
    for (int i = 1; i <= n + m; ++i) if (!din[i]) q.push(i);

    while (q.size())
    {
        auto t = q.front();
        q.pop();
        ans.push_back(t);

        for (int i = h[t]; ~i; i = ne[i])
        {
            int j = e[i];
            din[j]--;
            if (!din[j]) q.push(j);
        }
    }
}

int main()
{
    memset(h, -1, sizeof h);
    cin >> n >> m;
    for (int i = 1; i <= m; ++i)
    {
        // 建图（加入虚节点，平方->线性）
        memset(st, 0, sizeof st);
        int cnt, start = n, end = 1, ver = n + i;  // start记录最小的点，end记录最大的点，ver记录虚拟节点
        cin >> cnt;
        for (int i = 0; i < cnt; ++i)
        {
            int t;
            cin >> t;
            st[t] = 1;
            start = min(start, t);
            end = max(end, t);
        }

        // 把a->b的边拆成a->ver和ver->b
        for (int j = start; j <= end; ++j)
        {
            if (st[j]) add(ver, j, 1), din[j]++;
            else add(j, ver, 0), din[ver]++;
        }
    }

    // 拓扑排序得到更新的顺序
    topsort();

    // dp求最大值
    for (int i = 1; i <= n; ++i) dis[i] = 1;
    for (int i = 0; i < ans.size(); ++i)
    {
        int k = ans[i];
        for (int j = h[k]; ~j; j = ne[j])
        {
            int t = e[j];
            dis[t] = max(dis[t], dis[k] + w[j]);
        }
    }

    int res = 0;
    for (int i = 1; i <= n; ++i) res = max(res, dis[i]);
    cout << res << endl;
    return 0;
}

3.9 多源汇最短路

3.9.1 一般多源汇问题

acwing1125牛的旅行
题意： 农民John的农场里有很多牧区，有的路径连接一些特定的牧区。一片所有连通的牧区称为一个牧场。John将会在两个牧场中各选一个牧区，然后用一条路径连起来，使得连通后这个新的更大的牧场有最小的直径。现在请你编程找出一条连接两个不同牧场的路径，使得连上这条路径后，这个更大的新牧场有最小的直径。
1≤N≤150,0≤X,Y≤10^5^
题解:
本题要找最远的路径，可以这么考虑：最远的路径要不然是原来连通块内部最远路径，要不然是连接两个连通块的长度加上到两个端点最远的距离
因此只需要求出每个连通块内部最远距离，和连接两个连通块的距离+到两个端点的最大距离，二者做个max即可
代码：

#include

using namespace std;

typedef pair PDD;
const double INF = 1e30;
int const N = 155;

PDD grid[N];
double dis[N][N], maxd[N];
char g[N][N];
int n;

double get_dis(PDD x, PDD y)
{
    double dx = x.first - y.first, dy = x.second - y.second;
    return sqrt(dx * dx + dy * dy);
}

int main()
{
    // 读入坐标、坐标网
    cin >> n;
    for (int i = 0; i < n; ++i) cin >> grid[i].first >> grid[i].second;
    for (int i = 0; i < n; ++i) cin >> g[i];

    // 初始化每个点的距离
    for (int i = 0; i < n; ++i)
        for (int j = 0; j < n; ++j)
        {
            if (i == j) dis[i][j] = 0;
            else if (g[i][j] == '1') dis[i][j] = get_dis(grid[i], grid[j]);
            else dis[i][j] = INF;
        }
    
    // 计算每个点对间的距离
    for (int k = 0; k < n; ++k)
        for (int i = 0; i < n; ++i)
            for (int j = 0; j < n; ++j)
                dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
    
    // 计算每个连通块内部的最大距离
    double res1 = -1;
    for (int i = 0; i < n; ++i)
    {
        for (int j = 0; j < n; ++j)
        {
            if (dis[i][j] < INF / 2) maxd[i] = max(maxd[i], dis[i][j]);
        }
        res1 = max(res1, maxd[i]);
    }

    // 计算连接不同连通块的情况
    double res2 = INF;
    for (int i = 0; i < n; ++i)
        for (int j = 0; j < n; ++j)
        {
            if (dis[i][j] > INF/ 2) res2 = min(res2, maxd[i] + maxd[j] + get_dis(grid[i], grid[j]));
        }
    
    printf("%.6lf\n", max(res1, res2));
    return 0;
}

3.9.2 传递闭包问题

acwing343. 排序
题意： 给定 n 个变量和 m 个不等式。其中 n 小于等于26，变量分别用前 n 的大写英文字母表示。不等式之间具有传递性，即若 A>B 且 B>C ，则 A>C。
请从前往后遍历每对关系，每次遍历时判断：

• 如果能够确定全部关系且无矛盾，则结束循环，输出确定的次序；
• 如果发生矛盾，则结束循环，输出有矛盾；
• 如果循环结束时没有发生上述两种情况，则输出无定解。

题解： 传递闭包问题。 本题也可以不使用floyd，每次添加一条边的时候直接进行更新相关的点即可。这样可以把mn^3^优化到 mn^2^
代码：

#include

using namespace std;

int const N = 27;
int n, m;
int dis[N][N], st[N];

// 检查是否有解
int check()
{
    // 矛盾
    for (int i = 0; i < n; ++i)
        if (dis[i][i]) return 1;

    // 不确定
    for (int i = 0; i < n; ++i)
        for (int j = 0; j < i ; ++j)
            if (!dis[i][j] && !dis[j][i]) return 0;
    
    // 无解
    return 2;
}

// 打印当前最小的那个
void get_min()
{
    for (int i = 0; i < n; ++i)
    {
        bool flg = true;  // 初始认为i是最小的
        if (st[i]) continue;  // i必须没用过
        for (int j = 0; j < n; ++j)  // 看其他点是否能够走到i，要找到一个走不到i点的
        {
            if (!st[j] && dis[j][i])  // 如果j点能够走到i点，说明i点不是最小的
            {
                flg = false;
                break;
            } 
        }  // 如果是最小的
        if (flg)
        {
            printf("%c", i + 'A'); // 打印
            st[i] = 1;  // 记录
            break;
        }
    }
}

int main()
{
    while (cin >> n >> m && n && m)
    {
        memset(dis, 0, sizeof dis);
        int type = 0, t = 0;  // type=0:未确定，type=1:矛盾， type=2:有解，t记录是在哪个式子就判断出矛盾或者有解
        for (int i = 1; i <= m; ++i)
        {
            char str[5];
            cin >> str;
            int a = str[0] - 'A', b = str[2] - 'A';
            if (!type)  // 未确定才要需要继续
            {
                dis[a][b] = 1;  // 给a->b连边
                for (int x = 0; x < n; ++x)  
                {
                    if (dis[x][a]) dis[x][b] = 1;  // 如果x和a有边，那么x和b有边
                    for (int y = 0; y < n; ++y)  // 枚举y
                    {
                        if (dis[b][y]) dis[a][y] = 1;  // 如果b和y有边，那么a和y有边
                        if (dis[x][a] && dis[b][y]) dis[x][y] = 1;  // 如果x->a和b->y有边，那么x->y有边
                    }
                }
                type = check();  // 判断解的情况
                if (type) t = i;  // 记录是在哪个式子处判断出矛盾或者有解
            }

        }

        // 输出情况
        if (!type) printf("Sorted sequence cannot be determined.\n");
        else if (type == 1) printf("Inconsistency found after %d relations.\n", t);
        else 
        {
            printf("Sorted sequence determined after %d relations: ", t);
            memset(st, 0, sizeof st);
            for (int i = 0; i < n; ++i) get_min();  // 每次打印出最小的那个
            printf(".\n");
        }
    }
    return 0;
}

3.9.3 floyd找有向/无向最小环 O(n^3)

acwing344. 观光之旅
题意： 给定一张无向图，求图中一个至少包含3个点的环，环上的节点不重复，并且环上的边的长度之和最小。该问题称为无向图的最小环问题。你需要输出最小环的方案，若最小环不唯一，输出任意一个均可。
代码：

#include 

using namespace std;

int const N = 110;
int a[N][N], d[N][N], pos[N][N];
int n, m;
int ans;
vector path;

// 得到x->y这段之间的路径,不包括x和y这两个端点
void get_path(int x, int y) {
    if (pos[x][y] == 0) return ; // x与y之间没有点
    get_path(x, pos[x][y]);
    path.push_back(pos[x][y]);
    get_path(pos[x][y], y);
}

int main() {
    scanf("%d %d", &n, &m);
    
    // 距离初始化
    memset(a, 0x3f, sizeof a);
    for (int i = 1; i <= n; ++i) a[i][i] = 0;
    
    // 读入m条边
    for (int i = 1; i <= m; ++i) {
        int t1, t2, t3;
        scanf("%d %d %d", &t1, &t2, &t3);
        a[t1][t2] = a[t2][t1] = min(a[t1][t2], t3);
    }

    ans = 0x3f3f3f3f;
    memcpy(d, a, sizeof a);
    
    // 假设刚刚开始更新k，则k-1及其以下的情况全部更新完毕
    for (int k = 1; k <= n; ++k)  // k为最小环内编号最大的点
    {
        for (int i = 1; i < k; ++i) // i为最小环内第三大编号的点
            for (int j = i + 1; j < k; ++j)  // j为最小环内第二大编号的点
            {
                // 在k-1的情况下找到最小环
                if ((long long)d[i][j] + a[j][k] + a[k][i] < ans)  {
                    ans = d[i][j] + a[j][k] + a[k][i]; // 更新最小环的所有边权值和
                    
                    // 递归得到路径
                    path.clear();
                    path.push_back(i);
                    get_path(i, j);
                    path.push_back(j);
                    path.push_back(k);
                }
            }
            
        // 在k的情况下进行松弛操作
        for (int i = 1; i <= n; ++i)
            for (int j = 1; j <= n; ++j) {
                if (d[i][j] > d[i][k] + d[k][j]) {
                    d[i][j] = d[i][k] + d[k][j];
                    pos[i][j] = k;  // 记录i和j之间经过k点
                }
            }
    }
    
    // 打印答案
    if (ans != 0x3f3f3f3f) {
        for (int i = 0; i < path.size(); ++i)
            cout << path[i] << " ";
    }
    else cout << "No solution.\n";
    return 0;
}

3.9.4 floyd找恰好经过N条的最短距离

acwing345. 牛站
题意： 给定一张由T条边构成的无向图，点的编号为1~1000之间的整数。求从起点S到终点E恰好经过N条边（可以重复经过）的最短路。
代码：

#include 

using namespace std;

int const N = 201;
int n, t, s, e;
int cnt;  // 记录所有的点的数目
int num[N]; // 记录每一个点

// 定义一个矩阵
struct mat {
    int m[N][N];
}unit;

// 定义矩阵乘法
mat operator * (mat a, mat b) {
    mat res;
    memset(res.m, 0x3f, sizeof(res.m));
    for (int k = 1; k <= cnt; ++k)
        for (int i = 1; i <= cnt; ++i)
            for (int j = 1; j <= cnt; ++j)
                res.m[i][j] = min(res.m[i][j], a.m[i][k] + b.m[k][j]);
    return res;
}

// 矩阵快速幂
mat pow_mat(mat a, int n) {
    mat res = a;  // 这里不能使用快速幂，因为这里的矩阵乘法里面是加法，需要的是前一个的状态，而a^0这个状态无法退出a^1
    n--;
    while (n) {
        if (n & 1) res = res * a;
        a = a * a;
        n >>= 1;
    }
    return res;
}

int main() {
    cin >> n >> t >> s >> e;
    mat tmp;
    memset(tmp.m, 0x3f, sizeof(tmp.m));
    for (int i = 1; i <= t; ++i) {
        int a, b, c;
        scanf("%d %d %d", &c, &a, &b);
        if (!num[a]) num[a] = ++cnt;  // 标记点a出现过，同时记录所有出现的点的数目cnt
        if (!num[b]) num[b] = ++cnt;
        tmp.m[num[a]][num[b]] = tmp.m[num[b]][num[a]] = min(tmp.m[num[b]][num[a]], c);  // 记录a点和b点距离为c
    }
    mat ans = pow_mat(tmp, n); // 矩阵快速幂
    cout << ans.m[num[s]][num[e]] << endl;
    return 0;
}