快速幂 + 快速幂取模
文章目录
- 【快速幂】
- 1.原理
- 2.代码
- 【快速幂取模】
- 代码
- 【例题】
- LeetCode 50. Pow(x,n)
- HDU 6182 A Math Problem(卡精度)
- HDU 5363 Key Set(二项式定理)
- AcWing 875. 快速幂(模板)
- POJ 1995 Raising Modulo Numbers
- 洛谷 P1226 快速幂||取余运算(模板)
- AcWing 1289. 序列的第k个数
- 洛谷 P3197 越狱(容斥)
【快速幂】
快速幂就是快速算底数的 n n n 次幂。
时间复杂度为 O ( l o g N ) O(logN) O(logN), 与朴素的 O ( N ) O(N) O(N) 相比效率有了极大的提高。
1.原理
二分解释:
一般地, a n a^n an 的算法时间复杂度为 O ( n ) O(n) O(n),但是如果 n n n 为大数,则运行时间过长,效率不高。因此,使用二分的思想降低时间复杂度,使其降至 O ( l o g n ) O(logn) O(logn),则会使运行效率较大提升。二分思想如下图所示:

二进制解释:
假设我们要求 a b a^b ab,那么其实 b b b 是可以拆成二进制的。
例如当 b = 11 b=11 b=11 时, 11 11 11 的二进制是 1011 1011 1011,即 11 = 2 3 × 1 + 2 2 × 0 + 2 1 × 1 + 2 0 × 1 11 = 2^3×1 + 2^2×0 + 2^1×1 + 2^0×1 11=23×1+22×0+21×1+20×1;
那么 a 11 = a ( 2 0 + 2 1 + 2 3 ) = a 2 0 ∗ a 2 1 ∗ a 2 3 a^{11} = a^{(2^0+2^1+2^3)} = a^{2^0} * a^{2^1} * a^{2^3} a11=a(20+21+23)=a20∗a21∗a23
递归公式:
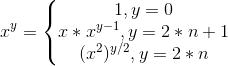
2.代码
1)常规求幂
int pow(int a, int b)
{
int r = 1;
while(b--)
r *= a;
return r;
}
2)快速求幂(一般)
int pow(int a, int b)
{
int r = 1, base = a;
while(b != 0)
{
if(b % 2)
r *= base;
base *= base;
b /= 2;
}
return r;
}
3)快速求幂(递归)
int pow(int m, int n)
{
if(n == 1)
return m;
int temp = f(m, n / 2);
return (n % 2 == 0 ? 1 : m) * temp * temp;
}
4)快速求幂(一般位运算)
int pow(int x, int n)
{
if(n == 0)
return 1;
else
{
while((n & 1) == 0)
{
n >>= 1;
x *= x;
}
}
int result = x;
n >>= 1;
while(n != 0)
{
x *= x;
if(n & 1)
result *= x;
n >>= 1;
}
return result;
}
5)快速求幂(更简洁的位运算)
int pow(int a, int b)
{
int r = 1, base = a;
while(b)
{
if(b & 1) // 取b二进制的最低位,1为奇数,0为偶数
r *= base;
base *= base;
b >>= 1; //把b的二进制右移一位,相当于除2
}
return r;
}
【快速幂取模】
就是给出 a , b , m ( 1 ≤ a , b , m ≤ 1 0 9 ) a, b, m\ (1 \leq a,b,m \leq 10^9) a,b,m (1≤a,b,m≤109) 三个数,快速计算 a b m o d m a^b\ mod \ m ab mod m 的值。
用到的公式:
- ( a b ) m o d c = ( a m o d c ) ( b m o d c ) (a^b) \ mod\ c = (a\ mod\ c)^{(b\ mod\ c)} (ab) mod c=(a mod c)(b mod c)
- a ∗ b m o d k = ( a m o d k ) ∗ ( b m o d k ) m o d k a * b\ mod\ k = (a\ mod\ k) * (b\ mod\ k)\ mod\ k a∗b mod k=(a mod k)∗(b mod k) mod k (积的取余等于取余的积取余)
以求 3 89 m o d 7 3^{89} \ mod\ 7 389 mod 7 为例:

代码
int Pow_Mod(int a, int b, int m)
{
int res = 1;
while(b)
{
if(b & 1)
res = (res * a) % m;
a = (a * a) % m;
b >>= 1;
}
return res;
}
当数非常大时,计算 (a*b)%m 使用 long long 也有可能爆精度,此时需要转乘法为加法,在模拟的同时不断求模。
LL Mult_Mod(LL a, LL b, LL m) // res = (a * b) % m
{
a %= m;
b %= m;
LL res = 0;
while(b)
{
if(b & 1)
res = (res + a) % m;
a = (a <<= 1) % m;
b >>= 1;
}
return res % m;
}
LL Pow_Mod(LL a, LL b, LL m) // res = (a ^ b) % m
{
LL res = 1;
LL k = a;
while(b)
{
if(b & 1)
res = Mult_Mod(res, k, m) % m;
k = Mult_Mod(k, k, m) % m;
b >>= 1;
}
return res % m;
}
【例题】
LeetCode 50. Pow(x,n)
题目链接:点击这里

先介绍一种精度最高的解法:
x n = e n l n x x^n = e^{nlnx} xn=enlnx
class Solution {
public:
double myPow(double x, int n) {
int sign = 1;
if(x < 0 && n & 1) sign = -1;
x = abs(x);
return sign * exp(n * log(x));
}
};
利用倍增思想,快速幂的递归写法:
class Solution {
public:
double fastPow(double x, long long n) {
if(n == 0) return 1.0;
double half = fastPow(x, n / 2);
if(n % 2 == 0) return half * half;
else return half * half * x;
}
double myPow(double x, int n) {
long long N = n;
if (N < 0) {
x = 1 / x;
N = -N;
}
return fastPow(x, N);
}
};
HDU 6182 A Math Problem(卡精度)
题目链接:点击这里
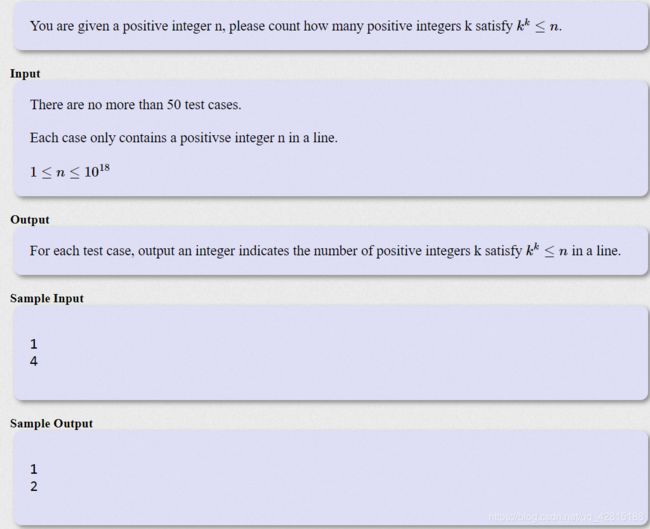
思路:这道题卡精度, 1 5 15 = 437 , 893 , 890 , 380 , 859 , 375 15^{15} = 437,893,890,380,859,375 1515=437,893,890,380,859,375。所以,必须控制枚举区间为 [ 1 , 15 ] [1,15] [1,15],否则会在求幂的中间过程中爆掉long long。
AC代码:
#includeHDU 5363 Key Set(二项式定理)
题目链接:点击这里
思路:
集合 S S S 中的元素是从 1 1 1 开始的连续的自然数,所以我们可以得到集合中的奇数个数 odd 与 偶数个数 even。
我们知道 偶数+偶数=偶数,奇数+奇数=偶数,因此奇数取偶数个,偶数任意取即可,得到下式:
AC代码:
#include知识补充:



AcWing 875. 快速幂(模板)
题目链接:点击这里

#includePOJ 1995 Raising Modulo Numbers
题目链接:点击这里
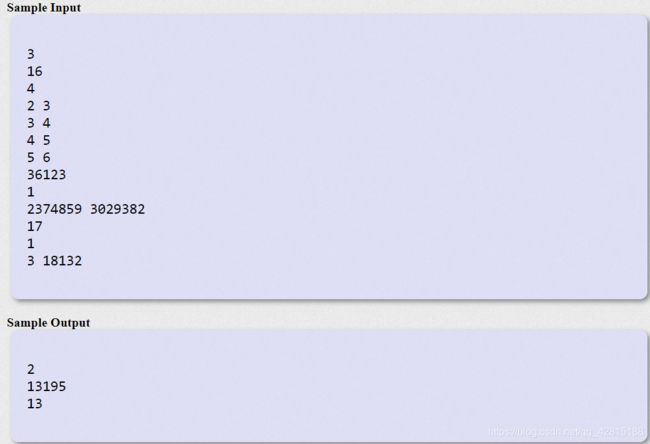
模运算与基本四则运算有些相似,但是除法例外。
( a + b ) % p = ( a % p + b % p ) % p (a + b)\ \%\ p = (a\ \%\ p + b\ \%\ p)\ \%\ p (a+b) % p=(a % p+b % p) % p
( a − b ) % p = ( a % p − b % p ) % p (a - b)\ \%\ p = (a\ \%\ p - b\ \%\ p)\ \%\ p (a−b) % p=(a % p−b % p) % p
( a ∗ b ) % p = ( a % p ∗ b % p ) % p (a * b)\ \%\ p = (a\ \%\ p * b\ \%\ p)\ \%\ p (a∗b) % p=(a % p∗b % p) % p
AC代码:
#include洛谷 P1226 快速幂||取余运算(模板)
题目链接:点击这里

最后一个测试数据如下,要特别注意 0 0 0 次幂:

因此,快速幂之后再取一次模。
AC代码:
#includeAcWing 1289. 序列的第k个数
题目链接:点击这里


分析:
给定 a , b , c a,b,c a,b,c 有没有可能既是等差数列,又是等比数列?
a + c = 2 ∗ b a + c = 2 * b a+c=2∗b
a c = b 2 ac = b^2 ac=b2
代入可得:
( 2 b − c ) c = b 2 (2b-c)c=b^2 (2b−c)c=b2
b 2 + c 2 − 2 b c = 0 b^2+c^2-2bc=0 b2+c2−2bc=0
( b − c ) 2 = 0 (b-c)^2=0 (b−c)2=0
b = c b=c b=c
所以,若 a , b , c a,b,c a,b,c 既是等差数列又是等比数列,那它一定是常数列,不影响答案。
AC代码:
#include洛谷 P3197 越狱(容斥)
题目链接:点击这里
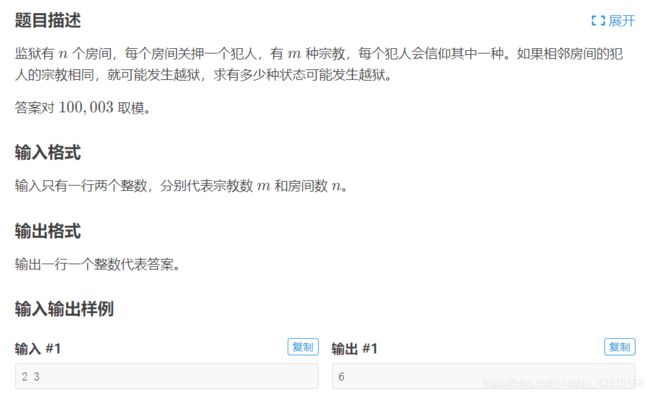

思路:
总方案数量 m ∗ m ∗ … ∗ m = m n m*m*…*m=m^n m∗m∗…∗m=mn
不发生越狱的方案数 m ∗ ( m − 1 ) ∗ . . . ∗ ( m − 1 ) = m ∗ ( m − 1 ) n − 1 m*(m-1)*...*(m-1) = m*(m-1)^{n-1} m∗(m−1)∗...∗(m−1)=m∗(m−1)n−1
故答案为 m n − m ∗ ( m − 1 ) n − 1 m^n-m*(m-1)^{n-1} mn−m∗(m−1)n−1
答案可能是负数,所以还需要把负余数转换成正余数 ( m n − m ∗ ( m − 1 ) n − 1 + m o d ) % m o d (m^n-m*(m-1)^{n-1}+mod)\ \%\ mod (mn−m∗(m−1)n−1+mod) % mod
AC代码:
#include