Expectation

Expectation

Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 524288/524288 K (Java/Others)

Problem Description

You are given an undirected graph consisting of $n$ vertices with $m$ weighted edges. We define the weight of a spanning tree as the bitwise AND of all edges’ weight in spanning tree.

Now select a spanning tree randomly, you should calculate the expected value of the weight of this spanning tree. You are required to print the result mod $998244353$. i.e., print $\frac{x}{y}$ mod $998244353$ where $\frac{x}{y}$ is the irreducible fraction representation of the result, where $y^{-1}$ denotes the multiplicative inverse of $y$ modulo $998244353$.

Input

The first line is an integer $t(1\le t\le 10)$, the number of test cases.

For each test case, there are two space-separated integers $n(2\le n\le 100)$ and $m(1\le m\le 10^4)$ in the first line, the number of nodes and the number of edges.

Then follows m lines, each contains three integers $u,v,w(1\le u,v,\le n,1\le w\le 10^9,u\ne v)$, space separated, denoting an weight edge between $u$ and $v$ has weight $w$.

Output

For each test case, output a single line with a single integer, denoting the answer.

Sample Input

1
3 3 
1 2 1 
1 3 1
2 3 1

Sample Output

1

知识点

矩阵树
对于一个无向图 G ，它的生成树个数等于其基尔霍夫Kirchhoff矩阵任何一个N-1阶主子式的行列式的绝对值。
例：

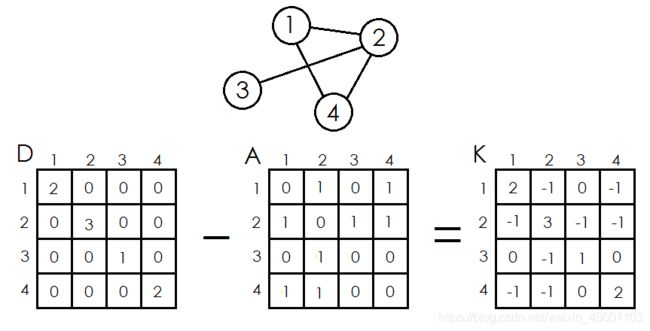
思路

题目要求每个生成树边权&&的期望值。
假设当前这颗生成树对二进制数的第$i$位有贡献，则这个位上的构成生成树的边权值一定是$1$，所以我们可以跑$31$位二进制数的，矩阵树，每个位上的贡献度等于，这个位上的生成树数量乘以这个位上的$2$次幂，最后再跑一边生成树计数，然后即可求得期望。

/***  Amber  ***/
#pragma GCC optimize(3,"Ofast","inline")
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
#define ls (rt<<1)
#define rs (rt<<1|1)
typedef long long ll;
typedef pair<int,int> pii;
template <typename T>
inline void read(T &x) {
     
    x = 0;
    static int p;
    p = 1;
    static char c;
    c = getchar();
    while (!isdigit(c)) {
     
        if (c == '-')p = -1;
        c = getchar();
    }
    while (isdigit(c)) {
     
        x = (x << 1) + (x << 3) + (c - 48);
        c = getchar();
    }
    x *= p;
}
template <typename T>
inline void print(T x) {
     
    if (x<0) {
     
        x = -x;
        putchar('-');
    }
    static int cnt;
    static int a[50];
    cnt = 0;
    do {
     
        a[++cnt] = x % 10;
        x /= 10;
    } while (x);
    for (int i = cnt; i >= 1; i--)putchar(a[i] + '0');
    puts("");
}
const double Pi=acos(-1);
const double eps=1e-6;
const int mod = 998244353;
const int inf = 0x3f3f3f3f;
const ll Inf = 0x3f3f3f3f3f3f3f3f;
const int maxn = 110;

int A[maxn][maxn],u[maxn * maxn],v[maxn * maxn],w[maxn * maxn];
int n,m;
inline void add(int u,int v,int w) {
     
    A[u][v] = (A[u][v] - w) % mod;
    A[v][v] = (A[v][v] + w) % mod;
}
ll qpow(ll a,ll b) {
     
    ll res = 1;
    while (b) {
     
        if (b & 1) res = res * a % mod;
        b >>= 1;
        a = a * a % mod;
    }
    return res;
}
ll inv(ll x){
     
    return qpow(x,mod-2);
}
ll gauss(int n) {
     
    ll res = 1;
    for (int i = 1; i <= n; i++) {
     
        for (int j = i; j <= n; j++) {
     
            if (A[j][i]) {
     
                for (int k = i; k <= n; k++) swap(A[i][k], A[j][k]);
                if (i != j) res = -res;
                break;
            }
        }
        if (!A[i][i]) return 0;
        for (ll j = i + 1, iv = inv(A[i][i]); j <= n; j++) {
     
            ll t = A[j][i] * iv % mod;
            for (int k = i; k <= n; k++) {
     
                A[j][k] = (A[j][k] - t * A[i][k] % mod + mod) % mod;
            }
        }
        res = (res * A[i][i] % mod + mod) % mod;
    }
    return res;
}
inline void work() {
     
    read(n);
    read(m);
    for (int i = 1; i <= m; i++) {
     
        read(u[i]);
        read(v[i]);
        read(w[i]);
    }
    ll ans = 0;
    for (int i = 0; i < 32; i++) {
     
        memset(A, 0, sizeof(A));
        for (int j = 1; j <= m; j++) {
     
            add(u[j], v[j], w[j] >> i & 1);
            add(v[j], u[j], w[j] >> i & 1);
        }
        ans = (ans + gauss(n - 1) * (1 << i) % mod) % mod;
    }
    memset(A, 0, sizeof(A));
    for (int j = 1; j <= m; j++) {
     
        add(u[j], v[j], 1);
        add(v[j], u[j], 1);
    }
    ans = ans * inv(gauss(n - 1)) % mod;
    print(ans);
}
int main() {
     
    //freopen("1.txt","r",stdin);
    int T = 1;
    read(T);
    while (T--) {
     
        work();
    }
    return 0;
}