模拟退火法和蚁群算法求解多元函数极值问题
模拟退火法和蚁群算法求解多元函数极值问题
目标函数:![]()
算法概述
模拟退火算法
模拟退火算法(Simulated Annealing,简称SA)的思想最早是由Metropolis等提出的。其出发点是基于物理中固体物质的退火过程与一般的组合优化问题之间的相似性。模拟退火法是一种通用的优化算法,其物理退火过程由以下三部分组成:
加温过程。其目的是增强粒子的热运动,使其偏离平衡位置。当温度足够高时,固体将熔为液体,从而消除系统原先存在的非均匀状态。
等温过程。对于与周围环境交换热量而温度不变的封闭系统,系统状态的自发变化总是朝自由能减少的方向进行的,当自由能达到最小时,系统达到平衡状态。
冷却过程。使粒子热运动减弱,系统能量下降,得到晶体结构。
加温过程相当于对算法设定初值,等温过程对应算法的Metropolis抽样过程,冷却过程对应控制参数的下降。这里能量的变化就是目标函数,我们要得到的最优解就是能量最低态。其中Metropolis准则是SA算法收敛于全局最优解的关键所在,Metropolis准则以一定的概率接受恶化解,这样就使算法跳离局部最优的陷阱。
SA算法的Metropolis准则允许接受一定的恶化解,具体来讲,是以一定概率来接受非最优解。举个例子,相当于保留一些“潜力股”,使解空间里有更多的可能性。对比轮盘赌法,从概率论来讲,它是对非最优解给予概率0,即全部抛弃。
模拟退火本身是求一个最小值问题,但可以转化为求最大值问题,只需要对目标函数加个负号或者取倒数。
原文链接:https://blog.csdn.net/lyxleft/article/details/82982567
蚁群算法
蚁群算法最早是由Marco Dorigo等人在1991年提出,他们在研究新型算法的过程中,发现蚁群在寻找食物时,通过分泌一种称为信息素的生物激素交流觅食信息从而能快速的找到目标,据此提出了基于信息正反馈原理的蚁群算法。
蚁群算法的基本思想来源于自然界蚂蚁觅食的最短路径原理,根据昆虫科学家的观察,发现自然界的蚂蚁虽然视觉不发达,但它们可以在没有任何提示的情况下找到从食物源到巢穴的最短路径,并在周围环境发生变化后,自适应地搜索新的最佳路径。
蚂蚁在寻找食物源的时候,能在其走过的路径上释放一种叫信息素的激素,使一定范围内的其他蚂蚁能够察觉到。当一些路径上通过的蚂蚁越来越多时,信息素也就越来越多,蚂蚁们选择这条路径的概率也就越高,结果导致这条路径上的信息素又增多,蚂蚁走这条路的概率又增加,生生不息。这种选择过程被称为蚂蚁的自催化行为。对于单个蚂蚁来说,它并没有要寻找最短路径,只是根据概率选择;对于整个蚁群系统来说,它们却达到了寻找到最优路径的客观上的效果。这就是群体智能。
原文链接:https://blog.csdn.net/wang_Number_1/article/details/52467567
模型假设
模拟退火算法
1)假设存在2个随机点,范围分别是-20-200,-200-20
2)假设每一次模拟的值都不同,但得到的都是在当前数值下的最优解。
3)假设每次运算都确实存在最优解。
4)取得的点均为整数
蚁群算法
1)假设存在2个随机点,范围分别是-20-200,-200-20
2)假设每一次模拟的值都不同,但得到的都是在当前数值下的最优解。
3)假设每次运算都确实存在最优解。
4)取得的点均为整数
5)碰到还没走过的路口,就随机挑选一条路走。同时,释放与路径长度有关的信息素。
6)信息素浓度与路径长度成反比。后来的蚂蚁再次碰到该路口时,就选择信息素浓度较高路径。
7)最优路径上的信息素浓度越来越大。
8)最终蚁群找到最优寻食路径
变量与符号说明
模拟退火算法
T0=1e11; % 初始温度,10的10次方!需要设定一个很大的温度。
T1=1e-3;% 终止温度
l=2; % 各温度下的迭代次数
q=0.993;%降温速率
Time % 计算迭代的次数
fun_value(point1) 目标函数
Metropolis()选取算法
new_point();%更新取点的函数
蚁群算法
m = 100; % 蚂蚁数量
alpha = 1.5; % 信息素重要程度因子
beta = 0.8; % 启发函数重要程度因子
rho = 0.1; % 信息素挥发因子
Q = 140; % 信息素释放增强系数
Eta = 1./D(1,:); % 启发函数
Tau = ones(1,t); % 信息素矩阵
Table = zeros(1,m); % 函数值记录表,每一行代表一个蚂蚁走过的路径
iter = 1; % 迭代次数初值
iter_max = 20; % 最大迭代次数
target_index1=zeros(1,m); %存放每个蚂蚁到达的点的坐标
Length_best = zeros(iter_max,1); % 各代最小函数值
Length_ave = zeros(iter_max,1); % 各代平均函数值
模型建立与算法设计
模拟退火法
初始化:取初始温度T0足够大,令T = T0,任取初始解S1。
对比GA、ACA、PSO之类的群优化算法,需要在解空间中产生多个个体,再继续寻优。而SA算法只需要一个点即可。
对当前温度T,重复第(3)~(6)步。
对当前解S1随机扰动产生一个新解S2。
此处随机的扰动没有定义。结合实际例子做选择。
计算S2的增量df = f(S2) - f(S1),其中f(S1)为S1的代价函数。
代价函数相当于之前群优化算法中讲的适应度函数。
若df < 0,则接受S2作为新的当前解,即S1 = S2;否则,计算S2的接受概率exp(-df/T), T是温度。随机产生(0,1)区间上均匀分布的随机数rand,若exp(-df/T) > rand,也接受S2作为新的当前解S1 = S2,否则保留当前解S1。
这是SA算法的核心部分,即有一定概率接受非最优解。
如果满足终止条件Stop,则输出当前解S1为最优解,结束程序,终止条件Stop通常取为在连续若干个Metropolis链中新解S2都没有被接受时终止算法或者是设定结束温度。否则按衰减函数衰减T后返回第(2)步,即被接受的新的解一直在产生,则我们要对问题进行降温,使得非最优解被接受的可能不断降低,结果愈发收敛于最优解。
原文链接:https://blog.csdn.net/lyxleft/article/details/82982567
蚁群算法
步骤1:对相关参数进行初始化,包括蚁群规模、信息素因子、启发函数因子、信息素挥发因子、信息素常数、最大迭代次数等,以及将数据读入程序,并进行预处理:比如将城市的坐标信息转换为城市间的距离矩阵。
步骤2:随机将蚂蚁放于不同出发点,对每个蚂蚁计算其下个访问城市,直到有蚂蚁访问完所有城市。
步骤3:计算各蚂蚁经过的路径长度Lk,记录当前迭代次数最优解,同时对路径上的信息素浓度进行更新。
步骤4:判断是否达到最大迭代次数,若否,返回步骤2;是,结束程序。
步骤5:输出结果,并根据需要输出寻优过程中的相关指标,如运行时间、收敛迭代次数等。
原文链接:https://blog.csdn.net/wang_Number_1/article/details/52467567
MATLAB代码
模拟退火法
函数1
function value = fun_value(point) %求函数值的函数
value=(point(1)+2*point(2)-7)^2+(2*point(1)+point(2)-5)^2;
end
函数2
function newpoint = new_point(~)%生成新点的函数
newpoint(1,1) =ceil(unifrnd(-10,200));
newpoint(2,1) =ceil(unifrnd(-200,10));
end
函数3
function [S,R] = Metropolis(S1,S2,T)
% S1: 当前解
% S2: 新解
% D: 距离矩阵(点的函数值)
% T: 当前温度
% S: 下一个当前解
% R: 下一个当前解的函数值
R1 = fun_value(S1); %计算点的函数值
R2 = fun_value(S2); %计算点的函数值
dC = R2 - R1; %计算函数值之差
if dC < 0 %如果函数值降低 接受新点
S = S2;
R = R2;
elseif exp(-dC/T)>= rand %以exp(-dC/T)概率接受新点
S = S2;
R = R2;
else %不接受新点
S = S1;
R = R1;
end
主程序
T0=1e11; % 初始温度,10的10次方!需要设定一个很大的温度。
T1=1e-3;% 终止温度
l=2; % 各温度下的迭代次数
q=0.993;%降温速率
Time = ceil(double(solve([num2str(T0) '*(0.9)^x = ',num2str(T1)]))); % 计算迭代的次数
%接下来初始化取的点的坐标
point1=zeros(2,1);
obj = zeros(Time,1);%代价函数值储存矩阵初始化
obj0=fun_value(point1);%计算初始值
count=0;%初始化计数值
track = zeros(2,Time);
while T0>T1
count =count+1;
point2=new_point();%更新取点的函数
% 2. Metropolis法则判断是否接受新解
[point1,R] = Metropolis(point1,point2,T0);%Metropolis 抽样算法
if count == 1 || R < obj(count-1)
obj(count) = R; %如果当前温度下函数值小于上一路程则记录当前函数值及对应的点
else
obj(count) = obj(count-1);%如果当前温度下函数值大于上一路程则记录上一函数值
end
track(:,count) = point1;
T0 = q * T0;
end
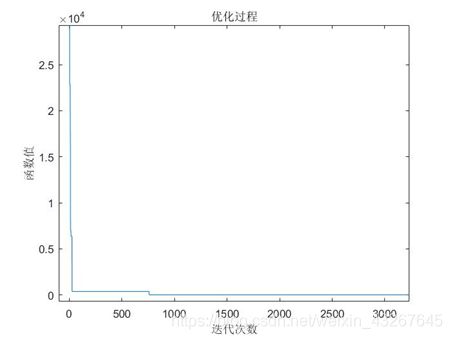
figure
plot(1:count,obj)
xlabel('迭代次数')
ylabel('函数值')
title('优化过程')
disp('最优解:')
S = track(:,end)
obj(end)
蚁群算法
运用该代码需加上fun_value函数
clear all
clc
% I. 清空环境变量
count1=1;
D=zeros(3,length(-200:10)^2);%第一行为函数值,第二三行为坐标
n=length(-200:10);
t=length(-200:10)^2;
for x=-10:200
for y=-200:10
D(1,count1)=fun_value([x,y])+4;
D(2,count1)=x;
D(3,count1)=y;
count1=count1+1;
end
end
m = 100; % 蚂蚁数量
alpha = 1.5; % 信息素重要程度因子
beta = 0.8; % 启发函数重要程度因子
rho = 0.1; % 信息素挥发因子
Q = 140; % 信息素释放增强系数
Eta = 1./D(1,:); % 启发函数
Tau = ones(1,t); % 信息素矩阵
Table = zeros(1,m); % 函数值记录表,每一行代表一个蚂蚁走过的路径
iter = 1; % 迭代次数初值
iter_max = 20; % 最大迭代次数
target_index1=zeros(1,m); %存放每个蚂蚁到达的点的坐标
Length_best = zeros(iter_max,1); % 各代最小函数值
Length_ave = zeros(iter_max,1); % 各代平均函数值
% V. 迭代寻找最佳路径
while iter <= iter_max
for i=1:m % 逐个蚂蚁路径选择
P=zeros(1,t);
for k=1:t % 逐个点选择
P(k) = Tau(k)^alpha* Eta(k)^beta;
end
p= P/sum(P);% 计算选取某一个点概率
Pc = cumsum(p);
target_index = find(Pc>= rand); %轮盘赌法
target = D(1,target_index(1));
target_index1(i)=target_index(1);
Table(i)=target;
end
Length_best(iter)=target
% 更新信息素
Delta_Tau = zeros(1,t);
% 逐个蚂蚁计算
for i = 1:m
Delta_Tau(target_index1(i)) = Delta_Tau(target_index1(i)) + Q/Table(i);
end
Tau = (1-rho) * Tau + Delta_Tau;
Table=zeros(1,m);
iter=iter+1
end
c=1:iter_max;
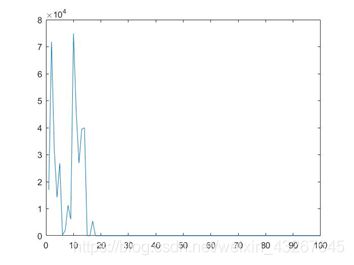
Length_best(end)
plot(c,Length_best,'-')
运行结果
模拟退火法
蚁群算法
优缺点及改进方向
模拟退火法
• 与遗传算法、粒子群优化算法和蚁群算法等不同,模拟退火算法不属于群优化算法,不需要初始化种群操作。
• 收敛速度较慢。因为1)它初始温度一般设定得很高,而终止温度设定得低,这样才符合物体规律,认为物质处于最低能量平衡点;2)它接受恶化解,并不是全程都在收敛的过程中。这一点可以类比GA中的变异,使得它不是持续在收敛的,所以耗时更多一些。
• 温度管理(起始、终止温度)、退火速度(衰减函数)等对寻优结果均有影响。比如T的衰减速度如果太快,就会导致可能寻找不到全局最优解。
原文链接:https://blog.csdn.net/lyxleft/article/details/82982567
蚁群算法
(1)采用正反馈机制,使得搜索过程不断收敛,最终逼近最优解。
(2)每个个体可以通过释放信息素来改变周围的环境,且每个个体能够感知周围环境的实时变化,个体间通过环境进行间接地通讯。
(3)搜索过程采用分布式计算方式,多个个体同时进行并行计算,大大提高了算法的计算能力和运行效率。
(4)启发式的概率搜索方式不容易陷入局部最优,易于寻找到全局最优解