回文字符串--manacher算法

回文字符串--manacher算法

回文串定义： “回文串” 是一个正读和反读都一样的字符串， 比如 “level ” 或者 “noon”等等就是回文串。回文子串，顾名思义，即字符串中满足回文性质的子串。

经常有一些题目围绕回文子串进行讨论，比如 HDOJ_3068_最长回文，求最长回文子串的长度。 朴素算法是依次以每一个字符为中心向两侧进行扩展， 显然这个复杂度是 O(N^2)的， 关于字符串的题目常用的算法有 KMP、 后缀数组、 AC 自动机， 这道题目利用扩展 KMP可以解答，其时间复杂度也很快 O(N*logN)。但是，今天笔者介绍一个专门针对回文子串的算法，其时间复杂度为 O(n)，这就是 manacher 算法。

大家都知道，求回文串时需要判断其奇偶性，也就是求 aba 和 abba 的算法略有差距。

然而， 这个算法做了一个简单的处理，很巧妙地把奇数长度回文串与偶数长度回文串统一考虑， 也就是在每个相邻的字符之间插入一个分隔符， 串的首尾也要加， 当然这个分隔符不能再原串中出现，一般可以用‘#’或者‘$’等字符。例如：

原串：abaab

新串：#a#b#a#a#b#

这样一来，原来的奇数长度回文串还是奇数长度，偶数长度的也变成以‘#’为中心的奇数回文串了。

接下来就是算法的中心思想，用一个辅助数组 P 记录以每个字符为中心的最长回文半径， 也就是 P[i]记录以 s[i]字符为中心的最长回文串半径。 P[i]最小为 1， 此时回文串为 s[i]本身。

我们可以对上述例子写出其 P 数组，如下

      新串： # a # b # a # a # b #

      P[  ] :    1 2 1 4 1 2 5 2 1 2 1

我们可以证明 P[i]-1 就是以 Str[i]为中心的回文串在原串当中的长度。

证明：

1、显然 L=2*P[i]-1 即为新串中以 Str[i]为中心最长回文串长度。

2、以 Str[i]为中心的回文串一定是以#开头和结尾的，例如“#b#b#”或“#b#a#b#”

所以 L 减去最前或者最后的‘#’字符就是原串中长度的二倍，即原串长度为(L-1)/2，化简得 P[i]-1。得证。

依次从前往后求得 P 数组就可以了，这里用到了 DP(动态规划)的思想，也就是求 P[i]的时候，前面的 P[]值已经得到了，我们利用回文串的特殊性质可以进行一个大大的优化。

我先把核心代码贴上：

for(i=1;ii)
	{
		p[i]=Min(p[2*id-i],MaxId-i);
	}
	else
	{
		p[i]=1;
	}
	while(a[i+p[i]]==a[i-p[i]])
	{
		p[i]++;
	}
	if(p[i]+i>MaxId)
	{
		MaxId=p[i]+i;
		id=i;
	}
}

定义数组p[i]表示以i为中心的(包含i这个字符)回文串半径长

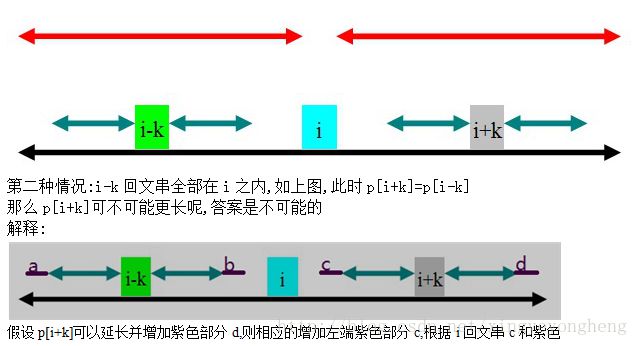
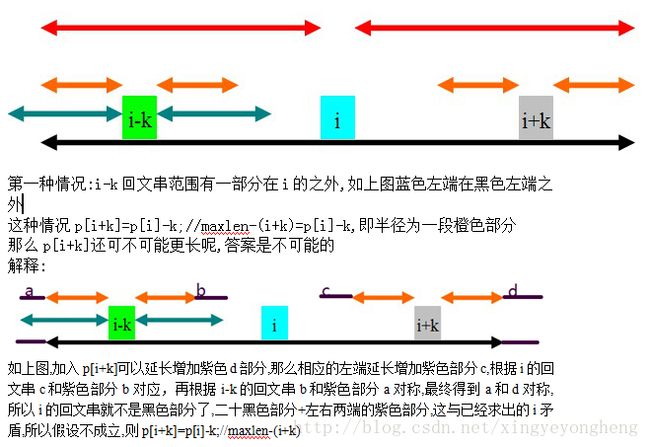
将字符串s从前扫到后for(int i=0;i

由于s是从前扫到后的,所以需要计算p[i]时一定已经计算好了p[1]....p[i-1]

假设现在扫描到了i+k这个位置,现在需要计算p[i+k]

定义maxlen是i+k位置前所有回文串中能延伸到的最右端的位置,即maxlen=p[i]+i;//p[i]+i表示最大的

分两种情况:

1.i+k这个位置不在前面的任何回文串中,即i+k>maxlen,则初始化p[i+k]=1;//本身是回文串

然后p[i+k]左右延伸,即while(s[i+k+p[i+k]] == s[i+k-p[i+k]])++p[i+k]

2.i+k这个位置被前面以位置i为中心的回文串包含,即maxlen>i+k

这样的话p[i+k]就不是从1开始

由于回文串的性质,可知i+k这个位置关于i与i-k对称,

所以p[i+k]分为以下3种情况得出

//黑色是i的回文串范围,蓝色是i-k的回文串范围,

贴上hdu-3068代码以供详细参考：

#include 
#include 
#include 
#include 

using namespace std;

const int maxn=110010;
char str1[maxn],str[2*maxn];
int p[2*maxn];

void Init(char *s)
{
    int i,j,len;

    len = strlen(s);
    str[0]='$';str[1]='#';
    for(i=0,j=2;ii)
            p[i]=min(p[2*id-i],maxlen-i);
        else
            p[i]=1;
        while(s[i+p[i]] == s[i-p[i]])
            p[i]++;
        if(p[i]+i>maxlen)
        {
            maxlen = p[i]+i;
            id = i;
        }
        if(p[i]>ans)
            ans = p[i];
    }
    return ans-1;
}
int main()
{
    while(scanf("%s",str1)!=EOF)
    {
        int k;
        memset(str,0,sizeof(str));
        memset(p,0,sizeof(p));

        Init(str1);

        k=manacher(str);
        printf("%d\n",k);
    }
    return 0;
}