数模2 Lingo解决线性规划问题
一、快速上手
- LP模型在Lingo中的一个典型输入方式:
1.以“MODEL:”开。
2.集合定义部分从(“SETS:”到”ENDSETS”)定义集合及其属性。
3.给出优化目标和约束。
4.数据定义部分从(“DATA:”到”ENDDATA”)。
5.以”END”结束。
- 要求:
- 每条语句后必须使用分号“;”结束。
- 用MODEL命令来作为输入问题模型的开始,格式为Model:statement (语句)end
- 目标函数必须由“min =”或“max =”开头。
- 简单例子:
# 线性规划
min=2*x1+3*x2;
x1+x2>=350;
x1>=100;
2*x1+x2<=600;
#非线性规划
Model: //正规形式 Model.... end
max=98*x1+277*x2-x1*x1-0.3*x1*x2-2*x2*x2;
x1+x2<100;
x1<=2*x2;
@gin(x1); //变量是整数
@gin(x2);
end
#0 1规划
Min=8*x11+13*x12+18*x13+23*x14+10*x21+14*x22+16*x23+27*x24+2*x31+10*x32+21*x33+26*x34+14*x41+22*x42+26*x43+28*x44;
x11+x12+x13+x14=1;
x21+x22+x23+x24=1;
x31+x32+x33+x34=1;
x41+x42+x43+x44=1;
x11+x21+x31+x41=1;
x12+x22+x32+x42=1;
x13+x23+x33+x43=1;
x14+x24+x34+x44=1;
end
int16
二、概念介绍
model:
!集合
sets:
warehouses/wh1..wh6/: capacity;
vendors/v1..v8/: demand;
links(warehouses,vendors): cost, volume;
endsets
!目标函数;
min=@sum(links: cost*volume);
!需求约束;
@for(vendors(J):
@sum(warehouses(I): volume(I,J))=demand(J));
!产量约束;
@for(warehouses(I):
@sum(vendors(J): volume(I,J))<=capacity(I));
!这里是数据;
data:
capacity=60 55 51 43 41 52;
demand=35 37 22 32 41 32 43 38;
cost=6 2 6 7 4 2 5 9
4 9 5 3 8 5 8 2
5 2 1 9 7 4 3 3
7 6 7 3 9 2 7 1
2 3 9 5 7 2 6 5
5 5 2 2 8 1 4 3;
enddata
end
1、Lingo中的集(“SETS:”到”ENDSETS”)
1) 定义原始集
# 集合名字[/成员列表/][:成员属性]
setname[/member_list/][:attribute_list];
# 1.显式罗列
students/John Jill, Rose Mike/: sex, age;#
# 2.隐式罗列
warehouses/wh1..wh6/: capacity;
2) 派生集
# 集合名字(父集),多个父集要逗号隔开
setname(parent_set_list)[/member_list/][:attribute_list];
# 例子
product/A B/;
machine/M N/;
week/1..2/;
allowed(product,machine,week):x;
2、Lingo中的数据(“DATA:”到”ENDDATA”)
1)简单的
sets:
set1/A,B,C/: X,Y;
endsets
data:
X=1,2,3;
Y=4,5,6;
enddata
2) 实时数据处理,每次都输入
data:
interest_rate,inflation_rate = .085 ?;
enddata
3) 数据部分有未知数
有时只想为一个集的部分成员的某个属性指定值,而让其余成员的该属性保持未知,以便让LINGO去求出它们的最优值。在数据声明中输入两个相连的逗号表示该位置对应的集成员的属性值未知。
capacity = ,34,20,,;3、函数
1) 数学函数
@abs(x) 返回x的绝对值
@sin(x) 返回x的正弦值,x采用弧度制
@exp(x) 返回常数e的x次方
@log(x) 返回x的自然对数
@lgm(x) 返回x的gamma函数的自然对数
@sign(x) 如果x<0返回-1;否则,返回1
@floor(x) 返回x的整数部分。当x>=0时,返回不超过x的最大整数;当x<0时,返回不低于x的最大整数。
@smax(x1,x2,…,xn) 返回x1,x2,…,xn中的最大值
2) 集循环函数
#函数名称(集合名字(变量)|条件 :表达式)
@function(setname[(set_index_list)[|conditional_qualifier]]:expression_list);
# for 循环
@for(number(I): x(I)=I^2);
# sum 循环
min=@sum(links: cost*volume);
3) 输入输出函数
可以把模型和外部数据比如文本文件、数据库和电子表格等连接起来。
data:
# 输入进去
capacity = @file('1_2.txt') ;
# 输出
@text('d:\out.txt')=days '至少需要的职员数为' start;
enddata4) 逻辑运算符
#not# 否定该操作数的逻辑值,#not#是一个一元运算符
#eq# 若两个运算数相等,则为true;否则为flase
#ne# 若两个运算符不相等,则为true;否则为flase
#gt# 若左边的运算符严格大于右边的运算符,则为true;否则为flase
#ge# 若左边的运算符大于或等于右边的运算符,则为true;否则为flase
#lt# 若左边的运算符严格小于右边的运算符,则为true;否则为flase
#le# 若左边的运算符小于或等于右边的运算符,则为true;否则为flase
#and# 仅当两个参数都为true时,结果为true;否则为flase
#or# 仅当两个参数都为false时,结果为false;否则为true、
5) 变量界定函数
变量界定函数实现对变量取值范围的附加限制,共4种:
@bin(x) 限制x为0或1
@bnd(L,x,U) 限制L≤x≤U
@free(x) 取消对变量x的默认下界为0的限制,即x可以取任意实数
@gin(x) 限制x为整数
在默认情况下,LINGO规定变量是非负的,也就是说下界为0,上界为+∞。@free取消了默认的下界为0的限制,使变量也可以取负值。@bnd用于设定一个变量的上下界,它也可以取消默认下界为0的约束。
综合实例
装配线平衡模型 一条装配线含有一系列的工作站,在最终产品的加工过程中每个工作站执行一种或几种特定的任务。装配线周期是指所有工作站完成分配给它们各自的任务所化费时间中的最大值。平衡装配线的目标是为每个工作站分配加工任务,尽可能使每个工作站执行相同数量的任务,其最终标准是装配线周期最短。不适当的平衡装配线将会产生瓶颈——有较少任务的工作站将被迫等待其前面分配了较多任务的工作站。
问题会因为众多任务间存在优先关系而变得更复杂,任务的分配必须服从这种优先关系。
这个模型的目标是最小化装配线周期。有2类约束:
① 要保证每件任务只能也必须分配至一个工作站来加工;
② 要保证满足任务间的所有优先关系。
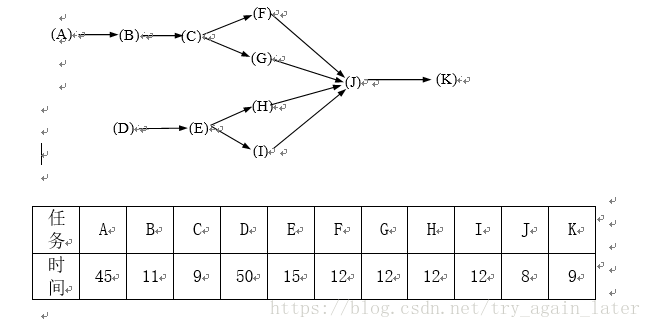
例 有11件任务(A—K)分配到4个工作站(1—4),任务的优先次序如下图。每件任务所花费的时间如下表。
Lingo代码
MODEL:
SETS:
!任务集合,有一个完成时间属性T;
TASK/ A B C D E F G H I J K/: T;
! 工作站集合;
STATION/1..4/;
!任务之间的优先关系集合(A 必须完成才能开始B,等等);
PRED( TASK, TASK)/ A,B B,C C,F C,G F,J G,J, J,K D,E E,H E,I H,J I,J /;
! X是派生集合TXS的一个属性。X(I,K)=1,则表示第I个任务指派给第K个工作站完成;
TXS( TASK, STATION): X;
ENDSETS
DATA:
!任务A B C D E F G H I J K的完成时间估计如下;
T = 45 11 9 50 15 12 12 12 12 8 9;
ENDDATA
!每一个任务必须指派到一个工作站,即满足约束①;
@FOR( TASK( I):
@SUM( STATION( K): X( I, K)) = 1);
!对于每一个存在优先关系的作业对来说,前者对应的工作站I必须小于后者对应的工作站J,即满足约束②;
@FOR( PRED( I, J):
@SUM( STATION( K): K * X( J, K) - K * X( I, K)) >= 0);
!对于每一个工作站来说,其花费时间必须不大于装配线周期;
@FOR( STATION( K):
@SUM( TXS( I, K): X( I, K)*T( I) ) <= CYCTIME);
!目标函数是最小化转配线周期;
MIN = CYCTIME;
!指定X(I,J) 为0/1变量;
@FOR( TXS: @BIN( X));
END
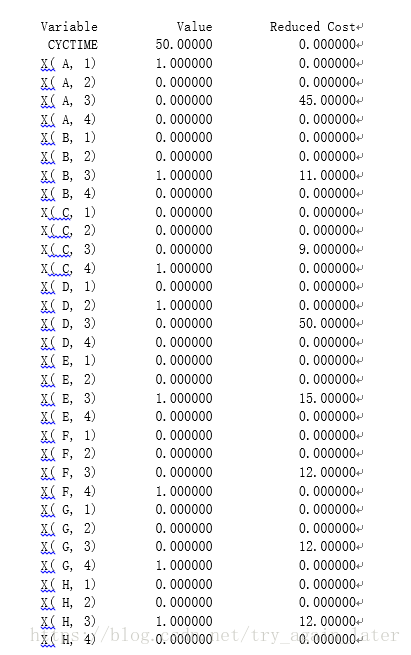
结果: