matlab 高级绘图函数
matlab高层绘图函数即是指Matlab提供了一系列的绘图函数,这些绘图函数使得用户不需要过多的考虑绘图的细节,只需要给出一些基本参数就能得到所需图形。与高级绘图函数的相对的是,低级绘图函数,这我们放在在后面探讨,这一篇博客我们就来探讨一下matlab高级绘图函数。
plot 函数
(1)当x和y是同维矩阵时,配对的x、y按对应列元素为横、 纵坐标分别绘制曲线,曲线条数等于矩阵的列数。例如, 在同一坐标中绘制3条幅值不同的正弦曲线,命令为 :
x=0:pi/10:2*pi;
y=sin(x);
plot([x;x;x]',[y;y*2;y*3]') (2)当x是向量,y是有一维与x同维的矩阵时,则绘制出多根 曲线,曲线条数等于y矩阵的另一维数,x被作为这些曲线 共同的横坐标。例如,在同一坐标中绘制3条幅值不同的 正弦曲线,命令也可以写成:
x=0:pi/10:2*pi;
y=sin(x);
plot(x,[y;y*2;y*3]) (3)当plot函数只有一个输入参数时,即plot(y) 时:
- 若y是实型向量,则以该向量元素的下标为横坐标、元素值为纵坐标画出一条连续曲线;
若y是复数向量,则分别以向量元素实部和虚部为横、纵坐标绘制一条曲线。
若y是实矩阵,则按列绘制每列元素值相对其下标的曲线, 曲线条数等于输入参数矩阵的列数;
- 若y是复数矩阵,则按列分别以元素实部和虚部为横、纵坐标绘制多条曲线。
(4)当plot函数有多个输入参数,且都为向量时,即plot(x1,y1,x2,y2,…,xn,yn)其中,x1和y1,x2和y2,……,xn和yn分别组成一组向量对,每一组向量对的长度可以不同。每一向量对可以绘制出一条曲线,这样可以在同一坐标内绘制出多条曲线。 例如,在同一坐标中绘制3条幅值不同的正弦曲线,命令也可以写成:
x=0:pi/10:2*pi;
y=sin(x);
plot(x,y,x,y*2,x,y*3) plotyy 函数
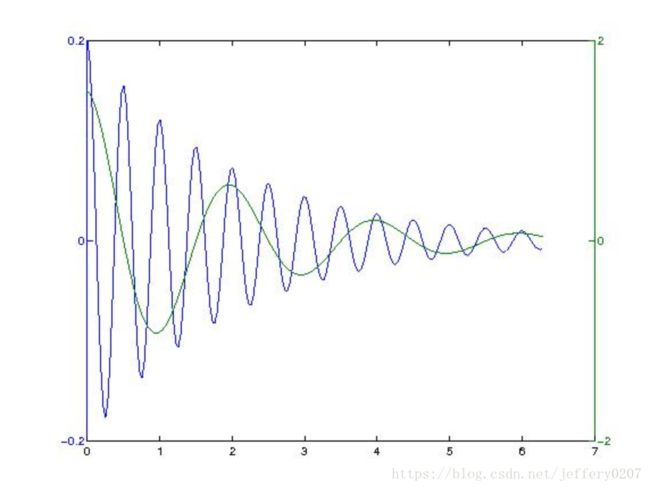
绘制出具有不同纵坐标标度的两个图形,可以使用plotyy 绘图函数。这种图形有利于图形数据的对比分析。 plotyy(x1,y1,x2,y2) , 其中,x1和y1对应一条曲线,x2和y2对应另一条曲线。 横坐标的标度相同,纵坐标有两个,左纵坐标用于x1、y1 数据对,右纵坐标用于x2、y2数据对。
clear all;
x=0:pi/100:2*pi;
y1=0.2*exp(-0.5*x).*cos(4*pi*x);
y2=1.5*exp(-0.5*x).*cos(pi*x);
plotyy(x,y1,x,y2); fplot函数
使用plot函数绘图时,都是等间隔取点。fplot函数可自适 应地对函数进行采样,调用格式为 :fplot(fname,lims,tol,optional)
- fname为函数名,以字符串形式出现。它可以是由多个分量函数构成的行向量,分量函数可以是函数的直接字符串,也可以是内部函数名或函数文件名,但自变量都必须为x
- lims为x、y的取值范围,以行向量形式出现, 取二元向量[xmin,xmax]时,x轴的范围被人为确定,取四元向量[xmin,xmax,ymin,ymax]时,x、y轴的范 围被人为确定。
- tol为相对允许误差,其系统默认值为2e-3 。
- optional参数与plot函数相同,即一些图形样式控制,我们后面再谈。
fplot('sin(x^2)/x',[-10,10],1e-4) subplot函数
在实际应用中,经常需要在一个图形窗 口内绘制若干个独立的图形,这就需要对图形窗口进行分割。分割后的图形窗口由若干个绘图区组成,每一个绘图区可以建立独立的坐标系并绘制图形。同一 图形窗口中的不同图形称为子图。 使用subplot(m,n,p)函数将当前 图形窗口分成m × n个绘图区,即 每行n个,共m行,区号按行优先编号,且选定第 p个区为当前活动区。在每一个绘图区允许以不同 的坐标系单独绘制图形。
x=-3:0.1:3;
subplot(2,2,[1 3]);
fplot('x-cos(x^3)-sin(2*x^2)',[-3,3]);
xlabel('(a)');
subplot(2,2,2);
y2 = sin(2.*x.^2);
plot(x,y2);
xlabel('(b)');
axis([-3 3 -1.2 1.2]);
subplot(2,2,4);
y3 = cos(x.^3);
plot(x,y3);
xlabel('(c)');
axis([-3 3 -1.2 1.2]);
grid on; 当然,值得注意的是,如果想在同一个画布上进行图形叠加,我们可以用hold on /off来进行控制。
e.g.
x=0:pi/100:2*pi;
y1=0.2*exp(-0.5*x).*cos(4*pi*x);
plot(x,y1);
hold on
y2=1.5*exp(-0.5*x).*cos(pi*x);
plot(x,y2);
hold off 对数坐标系绘图
semilogx(x1,y1,选项1,x2,y2,选项2,……)
semilogy(x1,y1,选项1,x2,y2,选项2,……)
- loglog(x1,y1,选项1,x2,y2,选项2,……)
semilogx函数使用半对数坐标,x轴为常 用对数刻度,而y轴仍保持线性刻度;semilogy函数也使用半对数坐标,y轴为常用对数刻度,而x轴仍保持线性刻度;loglog函数使用全对数坐标,x、y轴均采用常用对数刻度。
极坐标系绘图
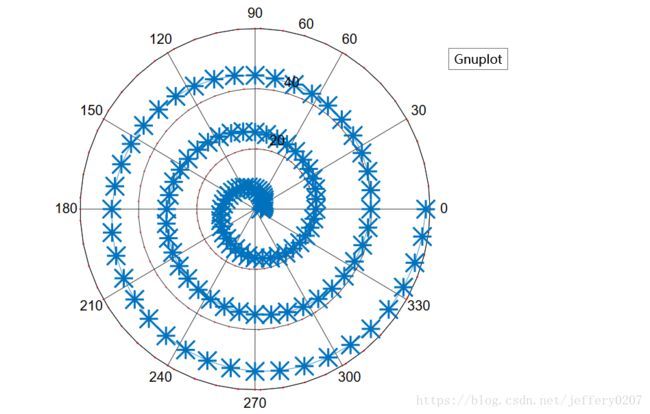
极坐标图用一个夹角和一段相对中心点—极点的距离来表示数据。MATLAB中用polar函数来绘制极坐标图,其调用格式为: polar(theta,rho,option) 其中,theta为极坐标极角,rho为极坐标矢径,option的内容与plot函数相似,放在后面探讨。
// 阿基米德螺旋线
t=0:pi/20:6*pi;
a=2;b=3;
r=a+b*t;
polar(t,r,'-*'); 二维统计分析图
bar函数
bar函数的基本用法与plot函数相似,其调用格式为 bar(x,width,style)。当x是m × n阶的矩阵时,绘制的条形图以分组或堆积的 形式表现。矩阵中每一行元素绘制在一组中,每一列元素 绘制在每组中相对应的位置上。
- width设置条形的 相对宽度和控制在一组内条形的间距,默认值为0.8;
- style指定条形的排列模式,类型有’group’(分组)和 ‘stack’(堆积),默认时采用’group’模式。
x=[51,82,34,47;67,78,68,90;78,85,65,50]';
subplot(1,2,1);
bar(x,'group');
title('Group');
axis([0 5 0 100]);
subplot(1,2,2);
barh(x,'stack');
title('Stack'); - bar函数绘制柱形图
- barh函数绘制水平条形图
- stem函数绘制杆图
- errorbar函数绘制误差条图
pie函数
饼图能反映每一数值相对于总数值的大小。MATLAB中绘 制饼图的函数是pie,其调用格式为 pie(x,explode) pie函数使用x中的数据绘制一个饼图,x可以是向量或矩阵。explode是与x同等大小的向量或矩阵,与explode的 非零值对应的部分将从饼图中心分离出来,默认explode 时,饼图是一个整体。
scatter函数
散点图是数据点在直角坐标系平面上的分布图。MATLAB 中绘制散点图的函数是scatter,其调用格式为: scatter(x,y,s,c,'filled')
- x、y、s和c为同等大小的向量。x和y用于定位数据点;
- s指定绘图点的大小,s也可以是一个标量,则所 有数据点同等大小;
- c指定绘图所使用的色彩,c也可以是 一个标量,所有数据点使用同一种颜色;
- ‘filled’表示填充 绘图点,默认时,数据点是空心的。
实心图
fill函数
实心图是将数据的起点和终点连成多边形,并填充颜色。 绘制实心图的函数是fill,其调用格式为 fill(x1,y1,选项1,x2,y2,选项2,…) 。fill函数按向量元素下标渐增次序依次用直线段连接x、y 对应元素定义的数据点。假若这样连接所得折线不封闭, 那么MATLAB将自动把该折线的首尾连接起来,构成封闭多边形,然后将多边形内部涂满指定的颜色。
n=6;
st=0:2*pi/n;:2*pi;
t=[st,st(1)]; %数据向量的首尾重合,使图形封闭
x=sin(t);
y=cos(t);
fill(x,y,'b');
axis([-1.5 1.5 -1.5 1.5])复数向量图
compass函数 和 feather函数
MATLAB中除可以用plot函数绘制复数向量图外,还可用 compass和feather函数,compass函数绘制围绕原点的罗盘图,feather函数绘制围绕x轴的羽毛图,其调用格式 为
compass(z);
compass(u,v);
feather(z);
feather(u,v);
//z为复数向量,u、v分别为复数向量的实部和虚部 举个例子:
theta = (-120:10:60)*pi/180;
r = 2*ones(size(theta));
[u,v] = pol2cart(theta,r);
//把极坐标或圆柱坐标转换为笛卡儿坐标
subplot(1,2,1);
compass(u,v);
title('compass');
subplot(1,2,2);
feather(u,v);
title('feather')图像精细控制
设置曲线样式
线型选择
曲线颜色
点标记符
图形标注
在绘制图形的同时,可以对图形加上一些说明,如图形名称、坐标轴 说明、图形某一部分的含义等,这些操作称为添加图形标注。
- title(图形名称)
- xlabel(x轴说明)
- ylabel(y轴说明)
- text(x,y,图形说明)
//指定坐标位置添加文字 - gtext(图形说明)
执行该命令时,十字坐标光标自动跟随鼠标移动,单击鼠标即 可将文本放置在十字光标处 - legend(图例1,图例2,……)
上述函数中的说明文字,除使用标准的ASCII字符外,还可使用LaTeX(LaTeX是一种十分流行的数学排版软件) 格式的控制字符,这样就可以在图形上添加希腊字母、数学符号、公式等内容。在MATLAB支持的LaTeX字符串中, 用\bf、\it、\rm控制字符分别定义黑体、斜体和正体字符, 受LaTeX字符串控制部分要加大括号{}括起来。
如果想在某个字符后面加一个上标,则可以在该字符后面 跟一个^引导的字符串。例如e^{axt}对应的标注效果为 eaxt,而e^axt对应的效果为eaxt。类似地可以定义下标,下标是由引导的,如X{12}对应 的标注效果为X12。
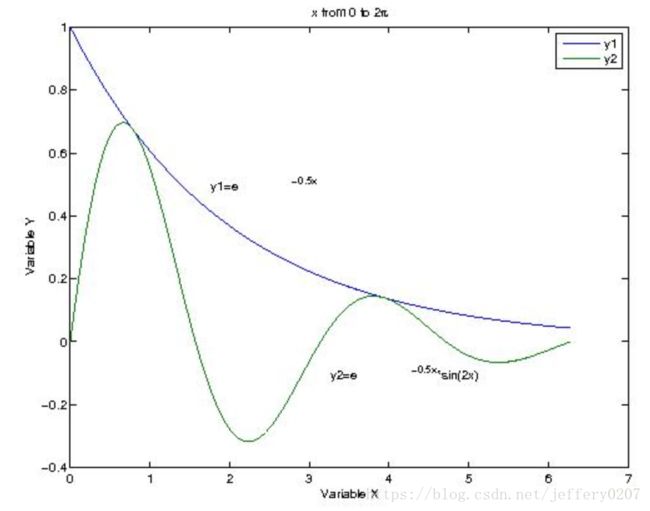
x=0:pi/100:2*pi;
y1=exp(-0.5*x);
y2=exp(-0.5*x).*sin(2*x);
plot(x,y1,x,y2);
title('x from 0 to 2{\pi}'); %加图形标题
xlabel('Variable X'); %加X轴说明
ylabel('Variable Y'); %加Y轴说明
text(1.5,0.5,'曲线y1=e^{-0.5x}'); %在指定位置添加图形说明
text(3,-0.1,'曲线y2=e^{-0.5x}*sin(2x)');
legend('y1','y2')坐标控制
axis([xmin xmax ymin ymax]);其他用法:
1. axis auto:使用默认设置
2. axis equal:纵、横坐标轴采用等长刻度
3. axis square:产生正方形坐标系(默认为矩形)
4. axis on/off:显示/取消坐标轴
说明:给坐标加网格线用grid命令来控制,加边框用box命令来控制。grid on/off命令控制是画还是不画网格线,box on/off命令控制是加还是不加边框线。