样本空间，随机事件基本概念 (概统1)

样本空间，随机事件概念(概统1)

概率论是一个难点，也是一个重点，难点主要是基本概念难以理清，看似很简单，但是很混乱，理不清。本小节是整理样本空间与随机事件的基本概念。

随机事件间的关系
包含 A ⊂ B，对立事件 A与 A¯¯¯¯ A ¯ ，互斥 AB= Φ Φ
随机事件，样本空间的关系

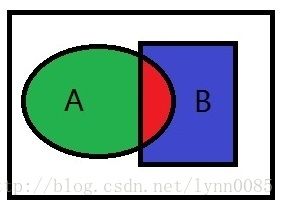
概念：整个框框表示所有情况的概率集合=1，
事件A发生的概率集合=P（A），事件B发生的概率集合=P（B）

事件种类：

1) A与B至少发生一个 ：

A ⋃ B = A + B – AB = 绿色 + 蓝色 + 红色
A与B一个都不发生：1-AUB = A∪B¯¯¯¯¯¯¯¯¯¯¯¯¯ A ∪ B ¯ = A¯¯¯¯∩B¯¯¯¯ A ¯ ∩ B ¯ = 所有白色区域

2) 两个同时发生：

A与B同时发生 A ⋂ B = AB =红色
除了A与B同时发生 = 1 - A ⋂ B=1 - A B = A∩B¯¯¯¯¯¯¯¯¯¯¯¯¯ A ∩ B ¯ = A¯¯¯¯∪B¯¯¯¯ A ¯ ∪ B ¯ = 红色以外 = 所有白色+绿色+蓝色

3)只发生一个:

只发生A: 绿色区域 = A - AB = AB¯¯¯¯ A B ¯
只发生B: 蓝色区域 = B – AB = BA¯¯¯¯ B A ¯

如果是独立事件：
只发生一个，
只发生A， 等于 绿色区域 = AB¯¯¯¯ A B ¯ =A-AB=A-B
只发生B， 等于 蓝色区域 = BA¯¯¯¯ B A ¯ =B-AB=B-A

对于独立事件： A-B=A-AB= AB¯¯¯¯ A B ¯ ; P(AB)=P(A)P(B)

---

4)引申出条件概率:

A发生的情况下，B发生的概率：

就是把A的椭圆定义为1，求AB相交区域，红色区域在A内部的概率
P(B|A)=P(AB)P(A|B))P(A)=P(AB)P(A) P ( B | A ) = P ( A B ) P ( A | B ) ) P ( A ) = P ( A B ) P ( A )

如果A与B两个是完全独立事件，则 P（AB）= P（A）P（B）
P(B|A)=P(AB)P(A)=P(A)P(B)P(A)=P(B) P ( B | A ) = P ( A B ) P ( A ) = P ( A ) P ( B ) P ( A ) = P ( B )
同理 P（A|B）= P（A）

如果A,B不是独立事件，那么 P（AB）≠ P（A）P（B）

==========

基本概念题

【例一】 设事件A与B同时发生时，事件C必发生，则

(A) P（C）≤ P（A）+P（B）-1
(B) P（C）≥ P（A）+ P（B）-1
(C) P（C） = P（AB）
(D) P（C） == P（A⋃B）

[知识点]： 1 代表什么？1是一个概率的最大值，不管是P(A)或者是P(AUB)或者是P(f(X))，最大值都是1。

上图中，1就代表了整个大框，在里面的全部小于1，最多等于1 ]

如图所示，A与B同时发生时是红色区域，那么C大于红色区域

P（A⋃B） = P（A）+ P（B）- P（AB）
红色部分，P（AB） = P（A） + P（B）– P（A⋃B）
P（AUB）<=1

所以，P（AB） >= P（A） + P（B） -1

P（ C） >P（AB）, 所以 P（C）> P（A） + P（B） – 1

答案：选 B

---

【例二】 设A B C是随机事件，A, C 互不相容，P（AB）= 12 1 2 ，P（C）= 13 1 3 ，则 P（AB| C¯¯¯¯ C ¯ ）= __ （考研真题）

[知识点]：条件概率的公式

P(B|A)=P(AB)P(A),P(C¯¯¯¯)=1−P(C) P ( B | A ) = P ( A B ) P ( A ) , P ( C ¯ ) = 1 − P ( C )

所以有

P(AB|C¯¯¯¯)=P(AB)P(C¯¯¯¯|AB)P(C¯¯¯¯)=P(AB)1−P(C)=121−13=1223=34 P ( A B | C ¯ ) = P ( A B ) P ( C ¯ | A B ) P ( C ¯ ) = P ( A B ) 1 − P ( C ) = 1 2 1 − 1 3 = 1 2 2 3 = 3 4

---

【例三】已知事件A,B仅发生一个的概率为0.4，且P（A）+ P（B） = 0.6，则A,B至少有一个不发生的概率为__。

[知识点]：什么叫做A,B仅发生一个？
A,B至少有一个不发生怎样表达？

A,B 至少有一个不发生 = 至少有一个x发生，就是求x1Ux2，这个x1就是 A¯¯¯¯ A ¯ , x2就是 B¯¯¯¯ B ¯ = A¯¯¯¯∪B¯¯¯¯ A ¯ ∪ B ¯ = A∩B¯¯¯¯¯¯¯¯¯¯¯¯¯ A ∩ B ¯ = AB¯¯¯¯¯¯¯¯ A B ¯

从图上看，至少有一个不发生 就是除了红色AB相交区域以外的区域
所以说，求出P（AB）就可以了

什么叫做A，B 仅发生一个？

A，B 仅发生一个 = 绿色区域 + 蓝色区域 = AB¯¯¯¯+BA¯¯¯¯ A B ¯ + B A ¯ = A u B - AB

P（ AB¯¯¯¯+BA¯¯¯¯ A B ¯ + B A ¯ ）= P（AUB）- P（AB）= P（A）+ P（B）- P（AB）- P（AB）
= P（A）+ P（B）- 2 P（AB）

P（ AB¯¯¯¯+BA¯¯¯¯ A B ¯ + B A ¯ ）=0.4
P（A）+ P（B）= 0.6
所以，
2 P（AB）= P（A）+ P（B）- P（ AB¯¯¯¯+BA¯¯¯¯ A B ¯ + B A ¯ ）=0.6-0.4=0.2
所以，P（AB）= 0.1
P（ AB¯¯¯¯¯¯¯¯ A B ¯ ）= 1 – P（A B）= 0.9

---

【例四】设事件A与事件B互不相容，则（） （考研真题）

（A）P（ AB¯¯¯¯¯¯¯¯ A B ¯ ）= 0
（B）P（AB）= P（A）P（B）
（C ）P（A）=1 –P（B）
（D ）P（ A¯¯¯¯∪B¯¯¯¯ A ¯ ∪ B ¯ ）= 1

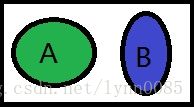
[知识点]：互不相容 ===》 A与B没有交集 ，P（AB）= 0，

如图，A 与 B 互不相容 ，两者没有交集

P(A¯¯¯¯∪B¯¯¯¯)=P(A∩B¯¯¯¯¯¯¯¯¯¯¯¯¯)=P(AB¯¯¯¯¯¯¯¯)=1−P(AB)=1−0=1 P ( A ¯ ∪ B ¯ ) = P ( A ∩ B ¯ ) = P ( A B ¯ ) = 1 − P ( A B ) = 1 − 0 = 1

所以选D

---

【例五】某奶厂生产A,B,C三种奶，经过调查，一城市居民中订购A奶的占45%，订购B奶的占35%，订购C奶的占30%，同时订购A,B两种奶的占10%，同时订购A,C两种奶的占8%，同时订购B,C两种奶的占5%，同时订购A,B,C三种奶的占3%，试算下列各事件的概率：

（1） 仅订购A奶的； （2）仅订购A, B奶的；
（3） 仅订购一种奶的； （4）恰好订购两种奶的；
（5）至少订购一种奶的； （6）不订购任何奶的；
（7）最多订购一种奶的

解题思路：还是把事件图摆出来，只不过把两种事件扩大为三种事件
P（A）=0.45，P（B）=0.35，P（C）=0.3
P（AB）=0.1，P（AC）=0.08，P（BC）=0.05 ，P（ABC）= 0.03

（1） 仅订购A奶的，相当于只发生一个，相当于 A 的绿色部分，

只不过两个事件推广到3个事件
两种事件：P（A1）= P（A）- P（AB）
三种事件：P（A1）=P（A）- P（AB）-P（AC）+P（ABC）；
注意，三种事件要加 P（ABC）

本题：P（A1）= P（A）- P（AB）- P（AC）+ P（ABC）= 0.45-0.1-0.08 + 0.03 = 0.30

（2） 仅订购A, B奶的；相当于浅蓝色部分；

仅订购A,B奶的与同时订购A,B两种奶的区别：
同时订购A,B两种奶，还包括了除了A,B两种奶，还订购了其他奶，比如还订购了C奶
仅订购A,B奶 = 同时订购A,B奶 – 订购A,B奶的同时还订购了其他奶

相当于两种事件的仅发生其中一种事件：P（A）= P（A）-P（AB）

P(ABC¯¯¯¯) P ( A B C ¯ ) = P（AB）- P（ABC）= 0.1 – 0.03 =0.07

（3） 仅订购一种奶的

P(X)=P(AB¯¯¯¯C¯¯¯¯)+P(BA¯¯¯¯C¯¯¯¯)+P(CA¯¯¯¯B¯¯¯¯) P ( X ) = P ( A B ¯ C ¯ ) + P ( B A ¯ C ¯ ) + P ( C A ¯ B ¯ )
P(AB¯¯¯¯C¯¯¯¯) P ( A B ¯ C ¯ ) = P（A）- P（AB）-P（AC）+P（ABC）=0.45 – 0.1 -0.08+0.03 = 0.3
P(BA¯¯¯¯C¯¯¯¯) P ( B A ¯ C ¯ ) = P（B）- P（BA）-P（BC）+P（ABC）=0.35 – 0.1 -0.05+0.03 = 0.23
P(CA¯¯¯¯B¯¯¯¯) P ( C A ¯ B ¯ ) = P（C）- P（AC）-P（BC）+P（ABC）=0.3 – 0.08 -0.05+0.03 = 0.2
最后P（X）=0.3+0.23+0.2=0.73

（4） 恰好订购两种奶的

等于全部相交部分，除去红色，除去红色部分三次；
注意，要减去红色部分三次；三次
P（X） = （P（AB）+ -P（ABC）） + （ P（BC）-P（ABC） ） + （P（AC）– P（ABC））
= 0.1 + 0.08 + 0.05 -3x0.03 = 0.14

（5） 至少订购一种奶的；

P（AUB）=P（A）+P（B） – P（AB）
P（AUBUC）=P（A）+P（B）+P（C）-P（AB）-P（AC）-P（BC）+P（ABC）
=0.45 + 0.35 + 0.3 -0.1-0.08-0.05+0.03 = 0.9

（6） 不订购任何奶的；

不订购任何奶=1- 至少订购一种奶
P（不订购任何奶） = 1 – P（至少订购一种奶） = 1.- 0.9 =0.1

（7） 最多订购一种奶的

P（最多订购一种奶）= 1- P（订购两种奶以上）
P（订购两种奶以上）
= P（AB）-P（ABC）+P（AC）-P（ABC）+P（BC）-P（ABC） + P（ABC）
=P（AB）+P（AC）+P（BC）-2P（ABC）
=0.1+0.08+0.05-2*0.03 = 0.17
P（最多订购一种奶） = 1- P（订购两种奶以上） = 1-0.17 =0.83

---

======
参考书目：张天德，叶宏 《星火燎原·概率论与数理统计辅导及习题精解》（浙大·第4版）第一章