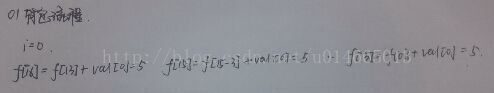01背包与完全背包（对比）

 

题意：

某Farmer最近买了一个书架，但是由于书架太高，Farmer够不到书架的顶端，现在屌丝Farmer开始通过将自己牧场的牛累起来这样使所累起来的牛能够高于书架的高度，但是努力使垒起来的牛的高度比书架的高度尽量能达到最小，求这个最小值。

解题思路：

初次看到这个题的时候真心的不知道怎么解，虽然感觉和背包有千丝万缕的关系，但是却不知道怎么转换，总是感觉变化了好像就变味了，知道瞥了眼解题报告，瞬间豁然开朗，柳暗花明。。。

其实就是将所有牛的高度加起来，与书架的高度做差得到V，这样再将V作为背包的体积，然后在转化为01背包就好了，此处注意在这里没有价值这个变量，所以在循环的时候，将体积作为价值就好了，这样的话装完后其实简单的要命，只不过当时没有转化过来，这可能是这道题的精髓吧

 

代码：

#include 
#include 
#include 
using namespace std;
int main()
{
    int T,N,V,V1;//T为测试数据个数 N为物品个数  V为背包所容纳的体积
	int f[1000005],vol[50], tem;//f记录i体积下的能盛下的最大价值    vol[i] 第i件物品的体积   val[i]记录第i件物品的价值	
	int i,j;
	scanf("%d %d",&N,&V1);
	
	int  sum=0;
	
	for(i = 0 ; i < N ; i++)
	{
		scanf("%d",&vol[i]);
		sum = sum + vol[i];
	}
	
	V=sum-V1;
	//cout<<"sum:"<= vol[i]; j--)
		{
		  tem = f[ j-vol[i] ] + vol[i];
			if( f[j] < tem )
                     f[j] = tem;
		}
	}
	
	cout<

 

我们看到的求最优解的背包问题题目中，事实上有两种不太相同的问法。有的题目要求“恰好装满背包”时的最优解，有的题目则并没有要求必须把背包装满。一种区别这两种问法的实现方法是在初始化的时候有所不同。

如果是第一种问法，要求恰好装满背包，那么在初始化时除了f[0]为0其它f[1..V]均设为-∞，这样就可以保证最终得到的f[N]是一种恰好装满背包的最优解。

如果并没有要求必须把背包装满，而是只希望价格尽量大，初始化时应该将f[0..V]全部设为0。

为什么呢？可以这样理解：初始化的f数组事实上就是在没有任何物品可以放入背包时的合法状态。如果要求背包恰好装满，那么此时只有容量为0的背包可能被价值为0的nothing“恰好装满”，其它容量的背包均没有合法的解，属于未定义的状态，它们的值就都应该是-∞了。如果背包并非必须被装满，那么任何容量的背包都有一个合法解“什么都不装”，这个解的价值为0，所以初始时状态的值也就全部为0了。

这个小技巧完全可以推广到其它类型的背包问题，后面也就不再对进行状态转移之前的初始化进行讲解。

小结

01背包问题是最基本的背包问题，它包含了背包问题中设计状态、方程的最基本思想，另外，别的类型的背包问题往往也可以转换成01背包问题求解。故一定要仔细体会上面基本思路的得出方法，状态转移方程的意义，以及最后怎样优化的空间复杂度。

 

 

 

对于此类经典的01背包，为了和完全背包区别开来，简单的看是不够的，并且很难想出其代码的区别和本质区别，下面就通过实际的数值来区分（其实代码的本质区别就是01背包从体积大的开始遍历，这样的话就不能一件物品多次放置，而完全背包就不同了，是从体积最小的开始遍历，这样的话就会出现一件物品多次放置的特点，这样也就凸显了两种背包的不同，但是这两种都是最基本的背包雏形）

假设测试用例：

物品编号	0	1	2	3	4
体积	3	4	5	6	7
价值	5	6	7	8	9

 01背包运行过程：

完全背包运行过程：

 

 

 具体完全背包案例: Piggy-Bank (完全背包)