2020年中国大学生数学建模竞赛备赛（十一）

5.2 最小二乘法

应用一：曲线拟合

线性最小二乘法是解决曲线拟合最常用的方法。基本思路是：

拟合的准则称为最小二乘准则，它是使$y_i(i=1,2,...,n)$与$f(x_i)$的距离差值的平方和最小。
1、系数$a_k$的确定。

经过推演得到：

其中：

2、函数$r_k(x)$的选取
面对已知的数据进行最小二乘拟合时，函数关系的选取很重要。确定两个变量之间的函数关系最常用的方法是：（1）通过机理分析，得到函数关系；（2）将已知的数据作图，通过图像直观判断。
常见的有：
最为稳妥的方法，也是最能够给论文添彩的方法，就是选择几种曲线分别拟合，然后比较，看哪条曲线的最小二乘指标$J$最小。

最小二乘法的MATLAB实现

1、解方程法

则编程的命令为：$A=R/Y$。
例题：已知$y=a+b\ast x^2$的经验公式，求对应的参数

//下面的数据是已知的
x=[19,25,31,38,44]';
y=[19.0,32.3,49.0,73.3,97.8]';
r=[ones(5,1),x.^2];
ab=r\y;
x0=19:0.1:44;
y0=ab(1)+ab(2)*x0.^2;
plot(x,y,'o',x0,y0,'r');

2、多项式拟合函数
如果取$[r_1(x),r_2(x),...r_m{+}_1(x)]=[1,x,...,x^m]$，即可以用如下的命令来拟合：

a=polyfit(x0,y0,m);//m为拟合多项式的次数
y=polyval(a,x);//计算多项式在x处的函数值

应用二 最小二乘优化

在无约束最优化问题中，目标函数由若干个函数的平方和构成，这类函数可以写成：

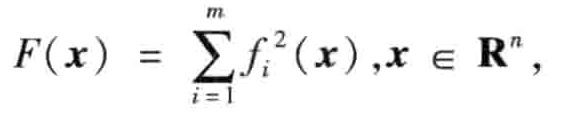
其中，$[x_1,...x_n{]}^T$,一般假设$m>=n$，把极小化这类函数的问题称为最小二乘优化问题。

最小二乘优化问题的MATLAB求解

1、$lsqlin$函数
基础模型：

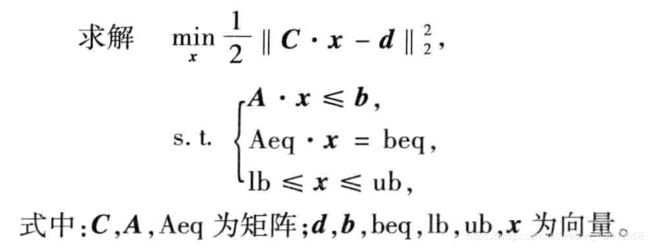
x=lsqlin(C,d,A,b,Aeq,beq,lb,ub,x0);

例题：

x=[19,25,31,38,44]';
y=[19.0,32.3,49.0,73.3,97.8]';
r=[ones(5,1),x.^2];
ab=lsqlin(r,y);
x0=19:0.1:44;
y0=ab(1)+ab(2)*x0.^2;
plot(x,y,'o',x0,y0,'r');

2、$lsqcurvefit$函数

x=lsqcurvefit(fun,x0,xdata,ydata,lb,ub,options);
//fun是定义函数F(x,xdata)的.m文件

3、$lsqnonlin$函数

x=lsqnonlin(fun,x0,lb,ub,options);
//其中fun是定义向量函数F(x)的.m文件

4、$lsqnonneg$函数

x=lsqnonneg(C,d,options);//求解非负的参数问题

参考文献

司守奎，孙玺菁. 数学建模算法与应用. 北京：国防工业出版社，2011.