神经网络架构搜索——可微分搜索（Cyclic-DARTS）

本文为微软研究院的NAS工作，论文题目：Cyclic Differentiable Architecture Search。 传统的DARTS在浅层网络（8 Cell）中搜索最优架构，然后在深层评价网络(20 Cell)中测量其性能。这导致架构搜索的优化与目标评价网络无关，发现的架构是次优的。针对搜索网络和评价网络的GAP问题，提出了一种新型的循环可微分架构搜索框架（CDARTS），在搜索网络和评价网络之间建立了循环反馈机制，并在CIFAR、ImageNet 和 NAS-Bench-201 上的实验和分析证明了所提出的方法的有效性。

• 论文链接：Cyclic Differentiable Architecture Search
• 源码链接：https://github.com/researchmm/CDARTS

摘要

近来，可微分架构搜索因其高效率、高性能的竞争优势引起了人们的极大关注。它在浅层网络中搜索最优架构，然后在深层评价网络中测量其性能。这导致架构搜索的优化与目标评价网络无关，发现的架构是次优的。为了解决这个问题，本文提出了一种新型的循环可微分架构搜索框架（CDARTS）。考虑到结构差异，CDARTS 在搜索网络和评价网络之间建立了循环反馈机制。首先，搜索网络生成一个初始拓扑进行评估，这样可以优化评价网络的权重。其次，搜索网络中的架构拓扑通过分类中的标签监督，以及来自评价网络的正则化通过特征提炼进一步优化。重复上述循环，搜索网络和评价网络共同优化，从而实现拓扑结构的进化，以适应最终的评价网络。在CIFAR、ImageNet 和 NAS-Bench-201 上的实验和分析证明了所提出的方法的有效性。

方法

预训练

这一阶段的目标是分别对搜索网络和评估网络进行预训练，并使其对数据产生适应性。具体来说，对于搜索网络，在训练前随机初始化架构超参数 $\alpha$。然后，在训练数据上优化权重 $w_S$，如下所示：

$$w_S^{\ast }=\underset{w_S}{\mathrm{argmin}}{\mathcal{L}}_{train}^S\left(w_S,\alpha \right)(1)$$

其中 ${\mathcal{L}}_{train}^S$ 为损失函数，$w_S^{\ast }$ 表示搜索网络的权重。对于图像分类问题，我们将 ${\mathcal{L}}_{train}^S$ 定义为交叉熵损失。

对于评估网络来说，其内部单元结构是通过对学习到的超参数 $\alpha$ 进行离散化生成的。评估网络的预训练是在val数据集下，通过优化以下目标函数进行的:

$$w_E^{\ast }=\underset{w_E}{\mathrm{argmin}}{\mathcal{L}}_{val}^E\left(w_E,\bar{\alpha }\right)(2)$$

联合学习

在这个优化阶段，搜索算法通过知识提炼，利用评价网络的特征反馈更新架构超参数$\alpha$。更具体地说，两个网络的联合优化公式为：

$$\begin{array}{r}{\alpha }^{\ast },w_E^{\ast }=\underset{\alpha ,w_E}{\mathrm{argmin}}{\mathcal{L}}_{val}^S\left(w_S^{\ast },\alpha \right)+{\mathcal{L}}_{val}^E\left(w_E,\bar{\alpha }\right)+\lambda {\mathcal{L}}_{val}^{S,E}\left(w_S^{\ast },\alpha ,w_E,\bar{\alpha }\right)\end{array}(3)$$

其中，最小化${\mathcal{L}}_{val}^S\left(w_S^{\ast },\alpha \right)$是在搜索网络中以固定权重 $w_S^{\ast }$ 优化架构超参数 $\alpha$，${\mathcal{L}}_{val}^E\left(w_E,\bar{\alpha }\right)$ 是在评估网络中以固定架构 $\alpha$ 优化权重 $w_E$， ${\mathcal{L}}_{val}^{S,E}\left(w_S^{\ast },\alpha ,w_E,\bar{\alpha }\right)$ 可以实现从评价网络到搜索网络的知识转移。${\mathcal{L}}_{val}^{S,E}(\cdot )$ 采用从评价网络中得到的评价特征作为监督信号，引导搜索网络中架构超参数 $\alpha$ 的更新。它是由一个软目标交叉熵函数构成：

$${\mathcal{L}}_{val}^{S,E}\left(w_S^{\ast },\alpha ,w_E,\bar{\alpha }\right)=\frac{T^2}{N}\sum _{i=1}^N\left(p\left(w_E,\bar{\alpha }\right)\log \left(\frac{p\left(w_E,\bar{\alpha }\right)}{q\left(w_S^{\ast },\alpha \right)}\right)\right)(4)$$

其中 N 为训练样本数，T 为温度系数（设为2）。这里，p(·)和q(·)分别代表评价网络和搜索网络的输出特征对数(output feature logits)，每个特征对数都计算为特征对数的软目标分布，如下公式所示：

$$\begin{array}{rl}p\left(w_E,\bar{\alpha }\right)& =\frac{\exp \left(f_i^E/T\right)}{{\sum }_j\exp \left(f_j^E/T\right)}\\ q\left(w_S^{\ast },\alpha \right)& =\frac{\exp \left(f_i^S/T\right)}{{\sum }_j\exp \left(f_j^S/T\right)}\end{array}(5)$$

其中 $f_i^E$ 和 $f_i^S$ 分别表示搜索网络和评价网络产生的特征。

• 公式 (3) 的联合训练实现了两个网络之间的知识转移。
• 公式 (4) 的优化通过提炼评价网络的特征知识，以指导搜索网络中架构超参数的更新。

此外，DARTS算法搜索出的结果存在 skip-connect 富集的问题，因为跳连可以实现快速的梯度下降。这本质上是一种架构搜索的过度拟合。为了解决这个问题，本文建议对架构超参数α中的跳连操作的权重施加 L1 正则化：

$${\mathcal{L}}_{Reg}={\lambda }^{\prime }\Vert \alpha {\Vert }_1(6)$$

其中，$\Vert \cdot {\Vert }_1$ 代表 l1正则，λ′ 为正的权衡系数。最后将式(3)与式(6)共同作为辅助项进行优化，以避免过度拟合。

值得注意的是，在评价网络的预训练过程中，即 公式（2）中，我们采用权值共享的策略来更新权重 $w_E$，以缓解训练不足的问题。具体来说，当离散化架构超参数 $\bar{\alpha }$ 更新时，评价网络的架构也会相应改变。新的评价网络的权重是用之前训练中继承的参数初始化的。换句话说，评估网络有一个 one-shot 的模型，它在有共同边的架构之间共享权重。这加快了新评估网络的收敛速度，从而提升了其在特征表示上的能力。这种权重共享策略与 single-path-one-shot 的方法不同，single-path-one-shot的方法是通过随机抽样来选择架构。相比之下，我们的方法选择架构由搜索网络进行优化，这就缓解了之前方法中训练不平衡的问题。

网络架构

Cyclic-DARTS的网络结构如上图所示。它由两个分支组成：一个有8个堆叠单元的搜索网络和一个有20个单元的评估网络。搜索网络和评估网络与之前的DARTS方法是相同的架构。

S-Net -> E-Net

对于信息传输，本文在两个分支之间建立了连接。更具体地说，有一个拓扑传输路径将发现的 Cell 架构从搜索分支传递到评估分支，上图中呈现的顶部粗箭头线。请注意，由于搜索空间的连续松弛，搜索网络发现的单元结构是一个全连接的图。换句话说，所有的候选操作都应用于计算图中每个节点的特征。当使用这种连续单元结构来构建新的评价网络时，我们需要先进行离散化处理。与之前 DARTS 工作相同，只保留之前所有节点收集到的所有候选操作中的 top-k（k = 2）最强操作。这个导出的离散单元结构作为评估分支的基本构件。

E-Net -> S-Net

另一方面，还有另一条特征提炼路径将评价分支的特征反馈传递给搜索分支，如上图中底部实心箭头所示。该反馈作为搜索网络的监督信号，以找到更好的单元结构。在细节上，本文使用评价网络的多级特征作为反馈信号，因为它们在捕捉图像语义上具有代表性。如上图所示的横向嵌入连接，多级特征将低分辨率、语义强的特征与高分辨率、语义弱的特征结合起来。这些特征来自于各阶段的输出，然后通过嵌入模块生成对应的特征对数。嵌入模块的功能是将密集的特征图投影到低维子空间中，通过软交叉熵层将得到的评价网络的对数作为搜索网络的监督信号，如公式（4）。

算法伪代码

实验

NAS-Bench-201

CIFAR

ImageNet

消融实验

组件分析

相关性分析

评估网络的深度

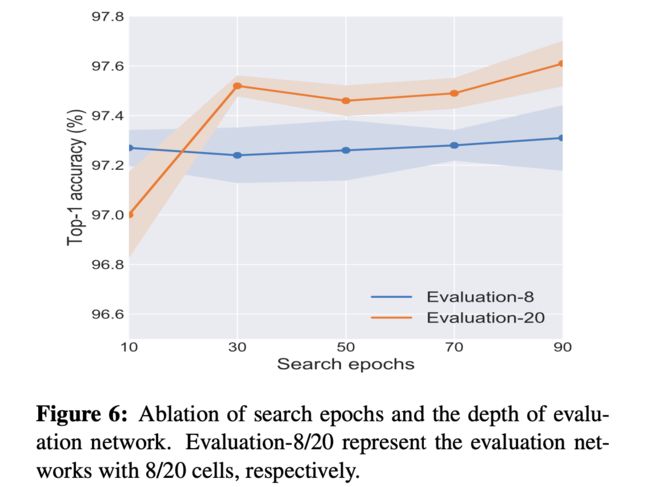
由于GPU内存的限制，DARTS的搜索网络只能堆叠 8 个单元，而评估网络则包含 20 个单元。 这带来了在PDARTS中研究的所谓的深度差距问题。 本文证明了在 Cycle-DARTS 的方法中不存在这种问题，因为将搜索和评估集成到一个统一的体系结构中。 如下所示，本文比较了评估网络中不同数量单元的性能。 它清楚地表明 20 单元评估网络（红线）的性能优于8单元网络（绿线）。 提出的两个网络的联合训练可以减轻深度差距的影响。

搜索轮数的影响

从上图可以看出，当搜索时期数接近 30 时，性能趋于饱和，评估网络的结构也趋于稳定。 因此，在实验中将搜索轮数设置为 30。

总结

在这项工作中，受 DARTS 中搜索和评估网络的分离问题的影响，提出了一种循环可微搜索算法，该算法将两个网络集成到一个统一的体系结构中。 交替联合学习使得能够搜索架构以适合最终评估网络。 实验证明了所提算法和搜索架构的有效性，它们在CIFAR，ImageNet和NAS-Bench-201上均具有竞争性能。

---