vtk基本数据结构与模型构建实例讲解

VTK基本数据结构

前面介绍了基本的vtk实例，这篇blog将重点学习VTK的基本数据结构，了解这些数据结构，有助于我们写出更有针对性的、更高效的可视化应用程序。

可视化数据的基本特点

我们的目的是要对数据进行可视化，因此有必要对可视化的数据特点作一了解。归纳起来，可视化数据具有如下一些特点：

l  离散性

为了让计算机能够获取、处理和分析数据，必须对无限、连续的空间体进行采样，生成有限的采样数据点，这些数据以离散点的形式存储，采样的过程是一个离散化的过程。

由于可视化数据的离散性特点，在某些离散点上有精确的值存在，但点与点之间的值则是不可知的，要得到采样点之外的其他点的值，只有通过插值(Interpolation)的方法获取。常用的插值方法是线性插值，要得到更精确的数值可以采用非线性插值，如B样条插值方法。

l  数据具有规则或不规则的结构(或者说结构化与非结构化)

可视化数据可以分为规则(Regular)和不规则(Irregular)或者说结构化(Structured)和非结构化(Unstructured)。规则结构数据点之间有固定的关联关系，可以通过这些关联确定每个点的坐标，不规则结构数据之间没有固定的关联关系。

对于规则结构的数据，存储时不必存储所有的数据点，只需存储起始点、相邻两点之间的间隔以及点的总数就可以保存完整的数据信息。对于不规则结构的数据，虽然不可以像规则结构的数据那样存储，但它也有自身的优势，即在数据变化频繁的区域可以密集表示，而数据变化不频繁的区域则稀疏表示。规则结构的数据可以在存储及计算时占优势，不规则结构的数据虽然存储和计算时不能像规则结构的那样高效，但它在数据表达方面相对而言则更加自由，更加细致、灵活的表现数据。

l  数据具有维度

可视化数据的第三个特点是拓扑维度(Topological Dimension)。可视化数据具有零维、一维、二维、三维等任意维度。如，零维的数据表现为点，一维数据表现为曲线，二维数据表现为曲面，三维数据表现为体等。数据的维度决定了数据可视化的方法，如，对于二维的数据，可以将数据存储到一个矩阵，然后再采用针对二维数据的可视化方法进行可视化(如等高图)。

几何数据结构模型

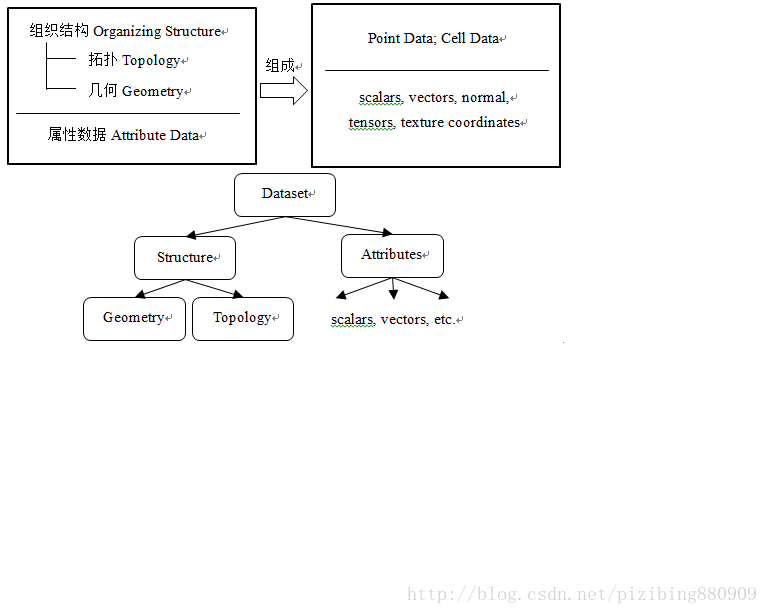
数据对象被组织成一种结构并且被赋予相应的属性值时就形成数据集(Dataset)。VTK里与数据集对应的类是vtkDataSet，该类从vtkDataObject直接派生。vtkDataSet由两个部分组成，即组织结构(Organizing Structure)以及与组织结构相关联的属性数据(Attribute Data)，下图描述了vtkDataSet各结构的详细构成。vtkDataSet是一个抽象基类，结构的实现及表达由其具体的子类来完成。

vtkDataSet的组织结构由拓扑结构(Topology)和几何结构(Geometry)两部分组成。拓扑结构描述了物体的构成形式，几何结构描述了物体的空间位置关系。换言之，点数据(Point Data)所定义的一系列坐标点构成了vtkDataSet(数据集)的几何结构；点数据的连接(点的连接先形成单元数据(Cell Data)，由单元数据再形成拓扑)就形成了数据集的拓扑结构。比如，我们想要在屏幕上显示一个三角形，首先我们必须定义三角形三个点的坐标(即Point Data，记三个点为P1, P2和P3)，然后将这三个点按照一定的顺序连接起来(P1-P2-P3，或者是P3-P2-P1的顺序)，这三个点定义了数据集的几何结构，它们的连接就构成了数据集的拓扑结构。亦即，点数据(Point Data)定义数据集的几何结构，单元数据(Cell Data)定义数据集的拓扑结构，要形成完整的数据集，必须有几何和拓扑两种结构。

关于拓扑、几何结构以及属性数据的更多解释：拓扑结构具有几何变换不变性。例如，说一个多边形是三角形，即指其拓扑结构，而给定的每个点的坐标，则为其几何结构。几何结构是一种空间描述，与空间变换有紧密联系，常见的变换有旋转、平移和缩放。属性数据是对拓扑结构和几何结构信息的补充，属性数据可以是某个空间点的温度值，也可以是某个单元的质量之类的。

 

vtkDataSet的结构组成

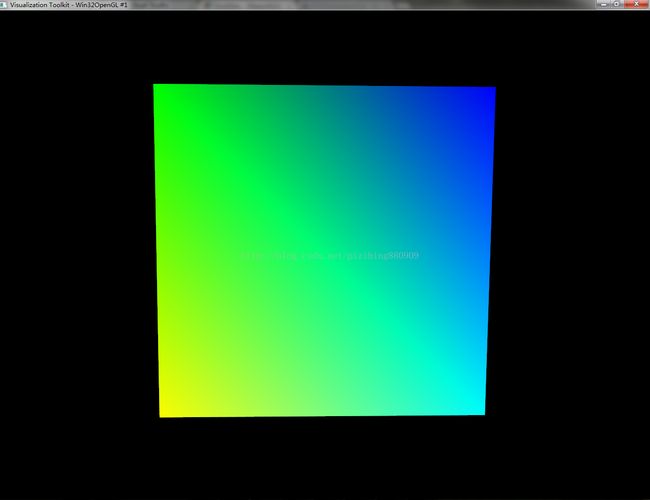
接下来我们通过例子说明怎么把几何结构和拓扑结构加入到数据集(vtkDataSet)中去。先看一下只有几何结构，没有拓扑结构的vtkDataSet。

 

下面用实例具体说明几何模型的构建：

#include "vtkActor.h"
#include "vtkCellArray.h"
#include "vtkDoubleArray.h"
#include "vtkFloatArray.h"
#include "vtkIntArray.h"
#include "vtkPointData.h"
#include "vtkPoints.h"
#include "vtkPolyData.h"
#include "vtkPolyDataMapper.h"
#include "vtkRenderWindow.h"
#include "vtkRenderWindowInteractor.h"
#include "vtkRenderer.h"

int main()
{
  int i;

  //模型顶点坐标array
  vtkFloatArray* pcoords = vtkFloatArray::New();

  //模型数据包含三个分量
  pcoords->SetNumberOfComponents(3);
  
  //顶点坐标包含的数据数目
  pcoords->SetNumberOfTuples(4);
  
  //模型几何顶点坐标
  float pts[4][3] = { {0.0, 0.0, 0.0}, {0.0, 1.0, 0.0},
                      {1.0, 0.0, 0.0}, {1.0, 1.0, 0.0} };
  for (i=0; i<4; i++)
    {
    pcoords->SetTuple(i, pts[i]);
    }

  //添加顶点坐标
  vtkPoints* points = vtkPoints::New();
  points->SetData(pcoords);

  //strip 模型单元构建
  vtkCellArray* strips = vtkCellArray::New();
  strips->InsertNextCell(4);
  strips->InsertCellPoint(0);
  strips->InsertCellPoint(1);
  strips->InsertCellPoint(2);
  strips->InsertCellPoint(3);

  //模型
  vtkIntArray* temperature = vtkIntArray::New();
  temperature->SetName("Temperature");
  temperature->InsertNextValue(10);
  temperature->InsertNextValue(20);
  temperature->InsertNextValue(30);
  temperature->InsertNextValue(40);
  
  //创建polydata数据集合
  vtkPolyData* polydata = vtkPolyData::New();
  polydata->SetPoints(points);
  polydata->SetStrips(strips);
  
  //添加属性值
  polydata->GetPointData()->SetScalars(temperature);
 
  //模型显示，并且设置数据mapper范围为0-40
  vtkPolyDataMapper* mapper = vtkPolyDataMapper::New();
  mapper->SetInput(polydata);
  mapper->SetScalarRange(0, 40);

  vtkActor* actor = vtkActor::New();
  actor->SetMapper(mapper);

  vtkRenderer* ren = vtkRenderer::New();
  ren->AddActor(actor);


  vtkRenderWindow* renWin = vtkRenderWindow::New();
  renWin->AddRenderer(ren);


  vtkRenderWindowInteractor* iren = vtkRenderWindowInteractor::New();
  iren->SetRenderWindow(renWin);
  iren->Initialize();
  iren->Start();


  pcoords->Delete();
  points->Delete();
  strips->Delete();
  temperature->Delete();
  vorticity->Delete();
  polydata->Delete();
  mapper->Delete();
  actor->Delete();
  ren->Delete();
  renWin->Delete();
  iren->Delete();
  return 0;
}