线性代数的本质(1)——基底、向量、线性变换、逆阵、行列式
我不知道多少人和我之前一样,在看到线性代数矩阵、向量之间的数值运算那些头发都要掉一圈。尤其是当我考研时考场上看到那两道线代题的时候人都傻了(20年数二)。但是在这考完后重新回来思考线性代数的本质的时候,发现这个真的是一个很有趣很奇妙的东西。
这篇文章不是以应试为目的的,而是在于讲解线性代数的本质,如果是只想学会怎样计算的同学可以不用浪费时间了。
当然由于本人水平有限,也还在漫漫求学路中,所以理解的可能不够透彻,解释的不够清楚,希望各位读者能够多多包涵,并提出宝贵的意见。
目录
- 零、基底
- 一、向量与线性变换
-
- 1. 向量
- 2. 线性变换
-
- 2.1 矩阵乘向量
- 2.2 矩阵乘矩阵
- 2.3 补充说明:矩阵
- 二、逆矩阵
- 三、行列式
-
- 1. 行列式几何意义
- 2. 行列式公式由来
- 3. 行列式为0
-
- 3.1 降维
- 3.2 没有逆阵
- 四、总结
- 五、参考
零、基底
在开始今天的话题前,要先引入“基底”(base vector,也称为基向量)这个概念。我不清楚读者知不知道这个,反正我无论是本科的时候听老师讲课,还是自己看同济大学的线性代数,亦或是考研的时候汤老师讲课,我都没有听到过这个概念,而基底这个概念又对我们从几何上理解线性代数的本质又有很重要的启示,所以我们先来谈谈基底。
基底的定义是:张成该空间的一个线性无关向量的集合。首先我们先来解读下这句话:
- 张成:既然要张成一个空间,那么证明我们向量的个数至少要大于等于空间的维数,就像2个向量无论如何也撑起不了一个三维空间一样;
- 空间:这里的空间有可能是点、线、平面、空间、超平面,即0维、1维、2维、3维等;
- 线性无关:我们这里先不从几何上讨论何为线性无关,那么线性无关就是任意一个向量都无法被其他向量表示,即没有冗余。
那么结合上面解释就会发现,基底的数量 = 空间的维数,本篇文章以二维为例(主要是三维的图好难画呜呜呜),读者可根据二维自行推导到高维。
我们通常取x正方向的单位长度和y正方向的单位长度作为两个基底,如下:
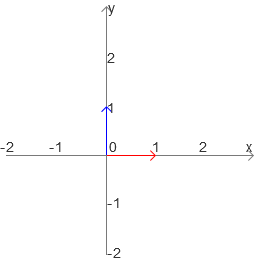
对应的矩阵就是np.mat(“1 0; 0 1”)。
![]()
当然,由于只要线性无关即可嘛,我们也可以取成下面这样,这些都是可以的,不过通常我们取上面这种情况,三维就同样是在z轴正方向取一个单位长度。

注:
- 我最开始的时候一直以为基底 = 基础解系,但是后来发现两者的关系其实是“基础解系是解空间的基底”;
- 注意上面的图中蓝色线条与红色线条的相对位置(即蓝色线条都在红色线条的左边),如果两者上下或者说前后顺序反了,那么说明空间发生了翻转;
- 一定是从原点出发的向量。
一、向量与线性变换
1. 向量
在线性代数中,向量就是有方向、有长度,并且起点始于原点的线段。
这里要先提出线性代数的两个很重要的法则,因为线性代数中每一个主题都围绕这两种运算:
那么我们接下来结合上基底的概念来看看在空间中向量加法与乘法。这里我们假定基底是上面第一个情形的基底。
-
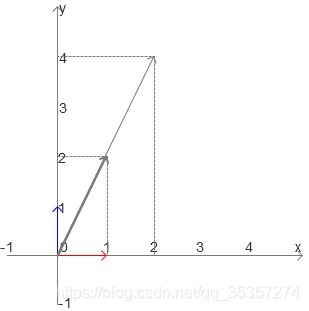
[2 1]T + [1 3]T = [3 4]T:[2 1]T就是x轴基底的2倍与y轴基底的1倍构成的向量,[1 3]T就是x轴基底的1倍与y轴基底3倍构成的向量,最后形成的[3 4]T就是在x轴走了2 + 1步,再沿着y轴方向走1 + 3,最后构成的向量(其实实际上应该是先向x轴走2步,向y轴走1步,再向x轴走1步,最后向y轴走3步),图示如下:

依据这两个法则,那么我们可以得出一个结论:基底可以表达出整个空间中的所有向量。
我们不妨想象一下,假设是以第一组基底为例,那么在这个二维平面中是不是任意一个向量都可以表达为在x轴的映射与在y轴的映射的组合?那么在x轴的映射是不是就是x轴基底的倍数,在y轴的映射是不是就是在y轴基底的映射?而选取的基底不同,一样可以用映射这个角度来思考,所以以上结论就证毕。
2. 线性变换
线性变换可以理解为一个函数,输入数据,最后输出数据(这几天在看神经网络,神经元超像这个的有没有)。而变换的含义就是指,某个向量经过了移动等方式,变换成了另一个向量。
注:只不过这个变换有几个点需要遵循:
- 原点不会移动;
- 每个格子之间保持平行于等间距。
第2点有点难理解,针对平行就是说,比如x = 1与x = 2这两条线是平行的,变换后这两条线依旧平行;而针对等间距就是说,比如我们的坐标轴上是以1为单位的格子,缩小一倍后,那么第一个格子应该是x = 0.5,第二个x = 1,而并非第一个格子x = 0.5,第二个格子x = 2。
依据这两点,那么我们就可以推论出,我们只需要记录基底更改后的位置,就可以得出整个空间的变换情况。这是因为整个空间都是随着这个变化而变化的。
或者用上面基底的结论来思考,基底进行了线性变换后,那么是不是仍然可以表达出整个空间中的任何向量?只不过基底变了,那么相应的其余位置也一起变了。
而何为线性,3B1B的解释是:固定某个向量,对另一个(组)向量进行伸长/收缩操作,最终会获得一条线(平面、超平面),就如下图所示,固定住[1 0]T,对[0 1]T进行伸长/收缩操作,最后可以获得x = 1这条线:

2.1 矩阵乘向量
而矩阵就是一种用来描述线性变换的工具,我们可以将矩阵的每一列看成是一个经过了线性变换后的基底,于是整个矩阵就变换为了经过了线性变换后基底的集合,而矩阵与向量的乘法就变为了,这个线性变换对这个向量的作用。我们用这个理论来讲解一个实际例子:
![]()
我们来看这个矩阵np.mat(“1 1; 0 1”),可以将这个矩阵看作是x轴的基底(1 0)T没有变化,而y轴基底变换到了(1 1)T,如下图所示:
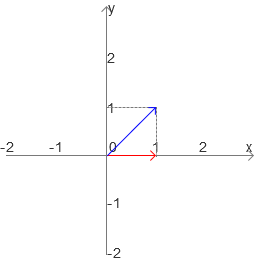
而新来的向量的x轴的变换受到了x轴基底的变换,于是得出如下公式:
1 * (1 0)T
向量y轴受到了y轴基底的变换,得出如下公式:
2 * (1 1)T
两者之和就得出了最终结果:
(1 0)T + (2 2)T = (3 2)T
这就是缩放基底再相加的思想。
我们把这个过程用另一个方法来写,就是我们平常使用的公式:
![]()
所以我们这里在最后再强调一下,矩阵与向量的乘法就是基向量的线性变换作用在新的向量上。
2.2 矩阵乘矩阵
我们从上面的角度来进行现在的思考,既然一个矩阵代表着一个线性变换,那么矩阵乘矩阵是不是就意味着,一个线性变换后又进行了一个线性变换呢?而最后获得的矩阵其实实际上就是这两个线性变换的一步就位的操作(就是两个线性变换相继作用)。
我们还是用一个实际的例子来看看这个问题,如下是这个计算结果:
![]()
注:矩阵乘法是从右向左读的,这里的意思是先经过了np.mat(“1 -2; 1 0”)的变换,后经过np.mat(“0 2; 1 0”)的变换。
我们首先考虑x轴基向量的变换,首先经过第一个线性变换的作用,x轴基向量变换为了(1 1)T,接着进行第二个线性变换,这里就转换为了上面说的矩阵乘向量问题,最后得出来x轴基向量变换到了(2 1)T。
同理,y轴基向量变换到了(0 -2)T。
2.3 补充说明:矩阵
上面关于矩阵的内容是一个基础的理解方式,但是矩阵最重要的机能是:指定了矩阵A,就确定了从向量到另外一个向量的映射。当然,映射是个很学术化的说法,平时也可以说是变换。
也就是说,当我们看到一个2×2的矩阵,那么就自然而然的想到x轴基向量移动(映射、变换)到了第一列的位置,y轴基向量移动(映射、变换)到了第二列的位置,然后这个变换就是整个空间的变换方式,这也可以看出其实线性代数就是对空间的操控。
而上面说到的矩阵乘向量就变为了一个向量在该空间操控下的映射(变换)情况;矩阵乘矩阵就是两个映射(变换)的合成。
二、逆矩阵
逆矩阵这个东西是我考研的时候最讨厌的东西,主要是计算量贼大,但是我们用另外几个角度来考虑逆矩阵这个问题。
首先我们从数值上来分析逆阵,我们来思考下,矩阵的运算中有没有除法?没有对吧,那么我们要怎样才能表达出这个除法?如果用单纯的数来描述的话,是不是x * x-1 = 1?那么逆阵也是同样的,A-1A = E(E是单位矩阵),所以数值上逆阵的作用就是说表达矩阵的除法。
其次我们从几何的角度再来考虑逆阵,我们对某个向量进行了线性变换,得到了一个新的向量,那么我们要怎样寻找原来的向量呢?是不是需要把新的向量给逆回去?这也就是逆阵的几何意义,将线性变换逆转。
三、行列式
1. 行列式几何意义
我们这里就先谈行列式的几何意义,最后再谈行列式的计算方法的由来(毕竟numpy都帮大家实现了计算了对吧)。
我们思考一下,经过线性变换,空间发生了变化,相应的面积也会发生变化,就如下图所示:
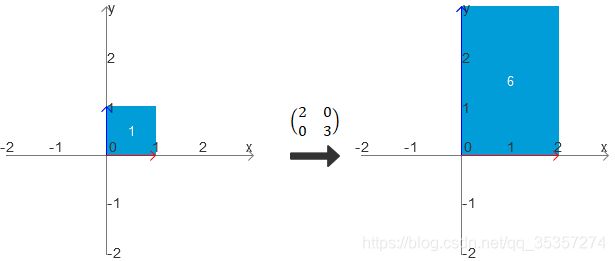
在x轴基向量扩大2倍,y轴基向量扩大3倍的情况下,面积扩大了6倍,而这个6正好就是线性变换后矩阵的行列式,由此可见,行列式的几何意义就是:线性变换改变面积(体积,超平面)的比例。
2. 行列式公式由来
相信经过应试教育的我们都知道行列式的公式如下:
![]()
那么我们从几何上来推理一下该公式,我们随意假设x轴基向量与y轴基向量在任意一个线性变化的作用下变换,得到如下结果:

由于我们所求是那个平行四边形的面积,从上面构建出整个长方形,得到每一部分区域,做减法就得结果了,整个减法如下:
(a + c) * (b + d) - 2 * (1/2ab) - 2 * (1/2cd) - 2cb = ad - bc
3. 行列式为0
3.1 降维
我们在有了上面的基础上来考虑下何为行列式为0。
行列式为0证明空间变换的比例为0,那么说明空间进行了收缩,也就是降维或者说数据冗余。如下图所示,两个向量共线,本来两个向量应该撑起一个平面的,但是现在只有一条线,所以就从二维变为了一维:

这同样也就是我们俗称的线性相关,于是我们将整个逻辑串联起来就是:
线性相关 = 有冗余 = 两个或多个向量在同一平面(点、空间、超平面) = 空间变化率为0 = 行列式为0
线性无关 = 没有冗余 = 任何一个向量都不会被其他向量表示 = 空间变化率不为0 = 行列式不为0
但是这里要说明一点,非方阵没有行列式,这个也很好理解,假设两维3个向量,那么我们说的面积变化究竟是哪一部分的面积变化?
3.2 没有逆阵
同样,行列式为0的矩阵没有逆阵。
我们用刚刚讲逆阵的知识来思考:
- 从数值上说就是不可能有数除以0得到其他数,而任何数乘以0都为0;
- 从几何上来谈就是当一个空间被降维后,我要如何在实数空间才能找到之前是哪个线性变换变换过来的?那么是不是会有无数个情况,但是却无法精准的定位到我们需要的那个?
这也就从另一个角度上告诉我们,降维很容易,但是升维无限难(阅读过《三体》的同学可以联想二向箔)。
四、总结
整理下本篇文章的内容,核心如下:
- 基底是张成该空间的一个线性无关向量的集合;
- 向量就是有方向、有长度,并且起点始于原点的线段;
- 线性代数最核心的法则就是加法与乘法;
- 基底可以表达出整个空间中的所有向量;
- 线性变换的实际意义,以及矩阵乘向量、矩阵乘矩阵的公式由来;
- 矩阵是映射;
- 数值上逆阵的作用是表达矩阵的除法,几何上意义是将线性变换逆转;
- 行列式的几何意义就是:线性变换改变面积(体积,超平面)的比例;
- 行列式公式由来;
- 线性相关 = 有冗余 = 两个或多个向量在同一平面(点、空间、超平面) = 空间变化率为0 = 行列式为0 = 没有逆阵;
- 线性无关 = 没有冗余 = 任何一个向量都不会被其他向量表示 = 空间变化率不为0 = 行列式不为0 = 有逆阵;
- 非方阵没有逆阵与行列式;
五、参考
[1]3Blue1Brown.【官方双语/合集】线性代数的本质 - 系列合集[EB/OL].https://www.bilibili.com/video/BV1ys411472E,2016-10-18.
[2][日]平冈和幸,堀玄.程序员的数学3线性代数[M].人民邮电出版社:北京,2016.3:5.