查找 --- 并查集
| Time Limit: 5000MS | Memory Limit: 65536K | |
| Total Submissions: 22601 | Accepted: 11134 |
Description
You know that there are n students in your university (0 < n <= 50000). It is infeasible for you to ask every student their religious beliefs. Furthermore, many students are not comfortable expressing their beliefs. One way to avoid these problems is to ask m (0 <= m <= n(n-1)/2) pairs of students and ask them whether they believe in the same religion (e.g. they may know if they both attend the same church). From this data, you may not know what each person believes in, but you can get an idea of the upper bound of how many different religions can be possibly represented on campus. You may assume that each student subscribes to at most one religion.
Input
Output
Sample Input
10 9 1 2 1 3 1 4 1 5 1 6 1 7 1 8 1 9 1 10 10 4 2 3 4 5 4 8 5 8 0 0
Sample Output
Case 1: 1 Case 2: 7
【题目来源】
Alberta Collegiate Programming Contest 2003.10.18
http://poj.org/problem?id=2524
【题目大意】
让你统计学校里总共有多少宗教。你不可以去问每个同学的宗教,有些同学不愿说出自己的宗教,解决这个问题的一个方法是:你可以去询问m对同学他们是否有相同的宗教。通过题目给的数据求出在
学校里有多少个宗教。你可以假设每个同学至少信仰一种宗教。
【题目分析】
简单的并查集水题。判断这两个同学是否属于同一宗教,然后统计。
AC代码:
#include<iostream> #include<cstring> #include<cstdio> #include<cstdlib> #include<cmath> #include<algorithm> #include<bitset> #define MAX 500000 using namespace std; int n,m; int a[MAX][2]; int parent[MAX]; int Find(int x) { if(x!=parent[x]) x=Find(parent[x]); return x; } int main() { int kase=1; while(scanf("%d%d",&n,&m),n||m) { int i,j; for(i=0;i<MAX;i++) parent[i]=i; for(i=0;i<m;i++) scanf("%d%d",&a[i][0],&a[i][1]); int cnt=0; int q,w; printf("Case %d: ",kase++); for(i=0;i<m;i++) { q=Find(a[i][0]); w=Find(a[i][1]); if(q!=w) parent[q]=w; } for(i=0;i<n;i++) if(parent[i]==i) cnt++; printf("%d\n",cnt); } return 0; }
下面是关于并查集的一些介绍,转自别人的博客。
并查集
并查集(Union-find Sets)是一种非常精巧而实用的数据结构,它主要用于处理一些不相交集合的合并问题。一些常见的用途有求连通子图、求最小生成树的 Kruskal 算法和求最近公共祖先(Least Common Ancestors, LCA)等。
使用并查集时,首先会存在一组不相交的动态集合 S={S1,S2,⋯,Sk},一般都会使用一个整数表示集合中的一个元素。
每个集合可能包含一个或多个元素,并选出集合中的某个元素作为代表。每个集合中具体包含了哪些元素是不关心的,具体选择哪个元素作为代表一般也是不关心的。我们关心的是,对于给定的元素,可以很快的找到这个元素所在的集合(的代表),以及合并两个元素所在的集合,而且这些操作的时间复杂度都是常数级的。
并查集的基本操作有三个:
- makeSet(s):建立一个新的并查集,其中包含 s 个单元素集合。
- unionSet(x, y):把元素 x 和元素 y 所在的集合合并,要求 x 和 y 所在的集合不相交,如果相交则不合并。
- find(x):找到元素 x 所在的集合的代表,该操作也可以用于判断两个元素是否位于同一个集合,只要将它们各自的代表比较一下就可以了。
并查集的实现原理也比较简单,就是使用树来表示集合,树的每个节点就表示集合中的一个元素,树根对应的元素就是该集合的代表,如图 1 所示。
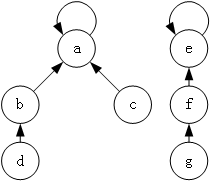
图 1 并查集的树表示
图中有两棵树,分别对应两个集合,其中第一个集合为 {a,b,c,d},代表元素是 a;第二个集合为 {e,f,g},代表元素是 e。
树的节点表示集合中的元素,指针表示指向父节点的指针,根节点的指针指向自己,表示其没有父节点。沿着每个节点的父节点不断向上查找,最终就可以找到该树的根节点,即该集合的代表元素。
现在,应该可以很容易的写出 makeSet 和 find 的代码了,假设使用一个足够长的数组来存储树节点(很类似之前讲到的静态链表),那么 makeSet 要做的就是构造出如图 2 的森林,其中每个元素都是一个单元素集合,即父节点是其自身:

图 2 构造并查集初始化
相应的代码如下所示,时间复杂度是 O(n):
|
1
2
3
4
5
6
|
const
int
MAXSIZE = 500;
int
uset[MAXSIZE];
void
makeSet(
int
size) {
for
(
int
i = 0;i < size;i++) uset[i] = i;
}
|
接下来,就是 find 操作了,如果每次都沿着父节点向上查找,那时间复杂度就是树的高度,完全不可能达到常数级。这里需要应用一种非常简单而有效的策略——路径压缩。
路径压缩,就是在每次查找时,令查找路径上的每个节点都直接指向根节点,如图 3 所示。
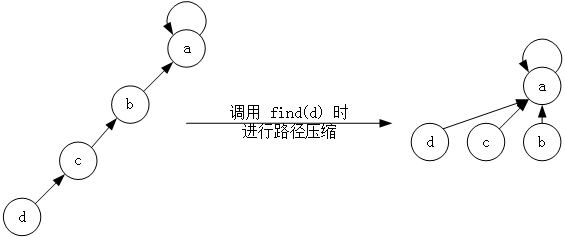
图 3 路径压缩
我准备了两个版本的 find 操作实现,分别是递归版和非递归版,不过两个版本目前并没有发现有什么明显的效率差距,所以具体使用哪个完全凭个人喜好了。
|
1
2
3
4
5
6
7
8
9
10
|
int
find(
int
x) {
if
(x != uset[x]) uset[x] = find(uset[x]);
return
uset[x];
}
int
find(
int
x) {
int
p = x, t;
while
(uset[p] != p) p = uset[p];
while
(x != p) { t = uset[x]; uset[x] = p; x = t; }
return
x;
}
|
最后是合并操作 unionSet,并查集的合并也非常简单,就是将一个集合的树根指向另一个集合的树根,如图 4 所示。
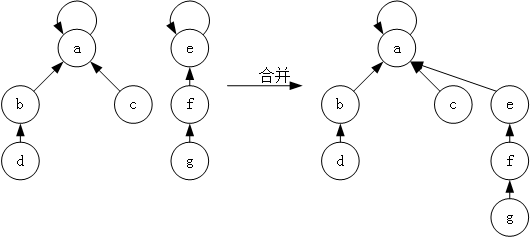
图 4 并查集的合并
这里也可以应用一个简单的启发式策略——按秩合并。该方法使用秩来表示树高度的上界,在合并时,总是将具有较小秩的树根指向具有较大秩的树根。简单 的说,就是总是将比较矮的树作为子树,添加到较高的树中。为了保存秩,需要额外使用一个与 uset 同长度的数组,并将所有元素都初始化为 0。
|
1
2
3
4
5
6
7
8
|
void
unionSet(
int
x,
int
y) {
if
((x = find(x)) == (y = find(y)))
return
;
if
(rank[x] > rank[y]) uset[y] = x;
else
{
uset[x] = y;
if
(rank[x] == rank[y]) rank[y]++;
}
}
|
下面是按秩合并的并查集的完整代码,这里只包含了递归的 find 操作。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
const
int
MAXSIZE = 500;
int
uset[MAXSIZE];
int
rank[MAXSIZE];
void
makeSet(
int
size) {
for
(
int
i = 0;i < size;i++) uset[i] = i;
for
(
int
i = 0;i < size;i++) rank[i] = 0;
}
int
find(
int
x) {
if
(x != uset[x]) uset[x] = find(uset[x]);
return
uset[x];
}
void
unionSet(
int
x,
int
y) {
if
((x = find(x)) == (y = find(y)))
return
;
if
(rank[x] > rank[y]) uset[y] = x;
else
{
uset[x] = y;
if
(rank[x] == rank[y]) rank[y]++;
}
}
|
除了按秩合并,并查集还有一种常见的策略,就是按集合中包含的元素个数(或者说树中的节点数)合并,将包含节点较少的树根,指向包含节点较多的树根。这个策略与按秩合并的策略类似,同样可以提升并查集的运行速度,而且省去了额外的 rank 数组。
这样的并查集具有一个略微不同的定义,即若 uset 的值是正数,则表示该元素的父节点(的索引);若是负数,则表示该元素是所在集合的代表(即树根),而且值的相反数即为集合中的元素个数。相应的代码如下所示,同样包含递归和非递归的 find 操作:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
const
int
MAXSIZE = 500;
int
uset[MAXSIZE];
void
makeSet(
int
size) {
for
(
int
i = 0;i < size;i++) uset[i] = -1;
}
int
find(
int
x) {
if
(uset[x] < 0)
return
x;
uset[x] = find(uset[x]);
return
uset[x];
}
int
find(
int
x) {
int
p = x, t;
while
(uset[p] >= 0) p = uset[p];
while
(x != p) {
t = uset[x];
uset[x] = p;
x = t;
}
return
x;
}
void
unionSet(
int
x,
int
y) {
if
((x = find(x)) == (y = find(y)))
return
;
if
(uset[x] < uset[y]) {
uset[x] += uset[y];
uset[y] = x;
}
else
{
uset[y] += uset[x];
uset[x] = y;
}
}
|
如果要获取某个元素 x 所在集合包含的元素个数,可以使用 -uset[find(x)] 得到。
并查集的空间复杂度是 O(n) 的,这个很显然,如果是按秩合并的,占的空间要多一些。find 和 unionSet 操作都可以看成是常数级的,或者准确来说,在一个包含 n 个元素的并查集中,进行 m 次查找或合并操作,最坏情况下所需的时间为 O(mα(n)),这里的 α 是 Ackerman 函数的某个反函数,在极大的范围内(比可观察到的宇宙中估计的原子数量 1080 还大很多)都可以认为是不大于 4 的。具体的时间复杂度分析,请参见《算法导论》的 21.4 节 带路径压缩的按秩合并的分析。