【笔记3-9】CS224N课程笔记 -递归神经网络和成分句法分析

【笔记3-1】CS224N课程笔记 - 深度自然语言处理
【笔记3-2】CS224N课程笔记 - 词向量表示 word2vec
【笔记3-3】CS224N课程笔记 - 高级词向量表示
【笔记3-4】CS224N课程笔记 - 分类与神经网络
【笔记3-5】CS224N课程笔记 - 依存分析
【笔记3-6】CS224N课程笔记 - RNN和语言模型
【笔记3-7】CS224N课程笔记 - 神经网络机器翻译seq2seq注意力机制
【笔记3-8】CS224N课程笔记 - 卷积神经网络

CS224n：深度学习的自然语言处理（2017年冬季）1080p https://www.bilibili.com/video/av28030942/

涉及到的论文：

Improved Semantic Representations From Tree-Structured Long Short-Term Memory Networks (Kai Sheng Tai, Richard Socher*, Christopher D. Manning)
https://arxiv.org/pdf/1503.00075.pdf

Deep Reinforcement Learning for Dialogue Generation (Jiwei Li, Will Monroe, Alan Ritter, Michel Galley, Jianfeng Gao and Dan Jurafsky)
https://arxiv.org/pdf/1606.01541.pdf

Parsing with Compositional Vector Grammars (Richard Socher John Bauer Christopher D. Manning Andrew Y. Ng)
https://nlp.stanford.edu/pubs/SocherBauerManningNg_ACL2013.pdf

Recursive Deep Models for Semantic Compositionality Over a Sentiment Treebank (Richard Socher, Alex Perelygin, Jean Y. Wu, Jason Chuang, Christopher D. Manning, Andrew Y. Ng and Christopher Potts)
https://nlp.stanford.edu/~socherr/EMNLP2013_RNTN.pdf

关键词：RNN, Recursive Neural Networks, MV-RNN, RNTN

本节讨论递归神经网络的多种变体及其在自然语言处理中的应用和成功。“RNN”在本文中是指递归神经网络（Recursive Neural Network），而不是循环神经网络（Recurrent Neural Network）。前者是后者的超集。下图是递归神经网络的一个例子。
tips：循环神经网络可以理解为只有右侧分支的递归神经网络

递归神经网络

本节笔记介绍一种新的模型递归神经网络，它是以前讨论过的循环神经网络的超集。递归神经网络非常适合具有嵌套层次结构和内在递归结构的设置。思考一个句子 “A small crowd quietly enters the historical church” 首先将句子分成名词短语、动词短语 “A small crowd” 和 “quietly enters the historical church”。在动词短语中又有一个名词短语，动词短语 “quietly enters” 和 “historical church”，这就是递归的一个例子。

语言的句法规则是高度递归的，因此RNN模型可以充分利用这种递归结构。用RNN建模的另一个好处是可以输入任意长度的句子，不论输入句子的长度如何，都能转换成相等规模的句子进行输出。

假设我们的任务将一个句子表示为与单词本身语义空间相同的向量。像“I went to the mall yesterday”、“We went shopping last week”和“They went to the store”这样的短语彼此之间的距离都非常近。前面介绍过训练unigram词向量的方法，如果对bigram、trigram等也做同样的处理可能很有效，但这种想法存在两个问题：1)单词有无限多种可能的组合。存储和训练无限数量的向量是不切实际的。2)有些单词的组合虽然在语言中完全可能出现，但可能不在培训/开发语料库中，所以永远学不会。

先讨论一下句子的语义和语法理解的区别。语义分析是对一个句子的意义的理解，能够在一个结构化的语义空间中把短语表示为一个向量，相似的句子非常近，不相关的句子非常远。语法理解是指已经确定了句子的基本语法结构，句子的哪一部分取决于哪一部分，哪些词在修饰哪些词等。这种理解的输出通常表示为一个解析树，如下图所示：

现在来看看最重要的问题：如果想要知道语义表征，拥有语法理解可能是一个优势，现在用下面的方法来处理这个语义组合任务。首先需要理解单词；然后需要知道单词是如何组合在一起的；最后可以通过利用前面的两个概念得到一个短语或句子的意思。

先从第一个基于这个原则的模型开始。假设有一个句子，我们知道这个句子的解析树，如上图所示，目标是使用一个简单的RNN来找出句子的编码，以及从句子的单词向量中得到一个情感得分。

一个简单的单层RNN

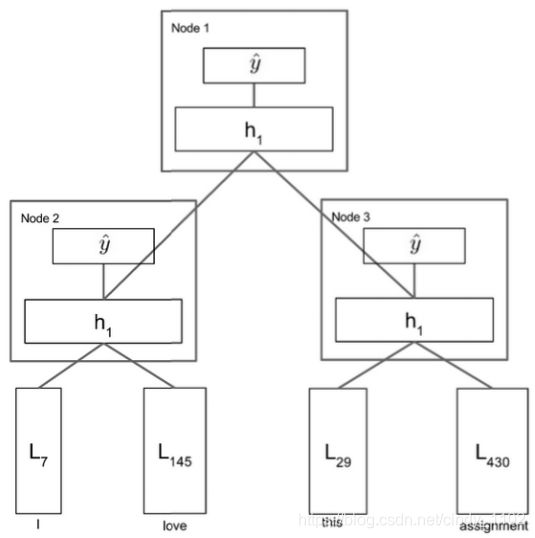
考虑上图中的模型。先获取一个句子解析树和句子单词向量，然后遍历该树。图中最低的节点是节点3，因此将 $L_{29}$ 和 $L_{430}$ 连接起来形成一个向量 $\in {\mathbb{R}}^{2d}$，并将其输入到网络中计算
$$\begin{gathered} h^{(1)}=tanh(W^{(1)}\left[\begin{array}{c}{L}_{29}\\ L_{430}\end{array}\right]+b^{(1)}) \\ {W}^{(1)}\in {\mathbb{R}}^{d\ast 2d},b^{(1)}\in {\mathbb{R}}^d,h^{(1)}\in {\mathbb{R}}^d \end{gathered}$$现在可以把 $h^{(1)}$ 看作是bigram “this assignment” 的同一个单词向量空间中的一个点，该空间不需要单独学习这个bigram的表示，而是直接从组成单词向量中派生出来。

现在取 $h^{(1)}$ 并将其放入softmax层中，获得一组情感得分（一组表示某种意义的离散已知类）在积极/消极情绪分析的情况下，有5个类，0表示强烈的消极，1表示消极，2表示中性，3表示积极，4表示强烈的积极。

现在对 “I” 和 “love” 做同样的处理，生成短语 “I love” 的向量 $h^{(1)}$。同样，计算该短语在语义类上的得分。最后需要合并两个短语 “I love” 和 “this assignment”。这里连接的是单词短语，而不是单词向量，即连接两个 $h^{(1)}$ 向量并计算：$$h^{(1)}=tanh(W^{(1)}\left[\begin{array}{c}{h}_{left}^{(1)}\\ h_{right}^{(1)}\end{array}\right]+b^{(1)})$$现在向量空间中有一个用于表示整个句子的向量。此外可以将这个$h^{(1)}$通过相同的softmax层，计算整个句子的情绪概率。

在以上的整个过程中，可以使用相同的矩阵W将所有单词连接在一起，得到一个非常有表现力的$h^{(1)}$，然后再次使用相同的矩阵W将所有短语向量连接起来，得到更深层的短语，但这样的想法过于简单，需要使用RNN的变体来进行处理。

Syntactically Untied SU-RNN

前面提到可以使用相同的W将名词短语和动词短语组合在一起，并将介词短语和另一个词向量组合在一起，但这个模型的功能较弱，需要进行改进。

一个想法是“从语法上解开”不同任务的权重。从理论上说，某一类输入的最优W与另一类输入的最优W不是完全相关的，所以使用的W应该是不一样的。这会增加要学习的权重矩阵，但能得到模型性能的较大提升。

如上图，模型取决于输入的语法类别。使用简单的概率上下文自由语法（Probabilistic Context Free Grammar，PCFG）确定类别（计算Penn Tree Bank上的汇总统计信息来学习）比如“the”总是一个 DT（determiner，限定词）

模型的主要区别是初始化了标识符的W，默认做法是对进来的两个单词向量求平均。模型会知道哪个向量更重要，以及向量的任何旋转或缩放都可以提高性能。从下图可知，经过训练的权重矩阵能学到实际含义，如DT-NP规则或限定词后跟名词词组(如“the cat” 或 “a man”)与限定词相比更强调名词词组。

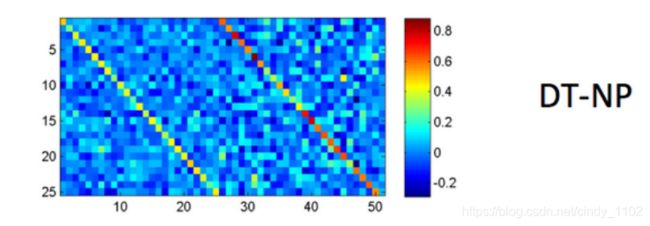
SU-RNN确实比之前讨论过的模型表现更好，但它的表现力还不够。考虑修改单词，比如副词“very”，副词的字面意思是“用于强调”。只做线性插值时，无法得到一个强调其他向量的向量，或“缩放”任何其他向量。此时，需要用到一个词对另一个词的乘法。一个方法是利用字矩阵，另一个是利用二次方程的典型仿射。

MV-RNN’s (Matrix-Vector Recursive Neural Networks)

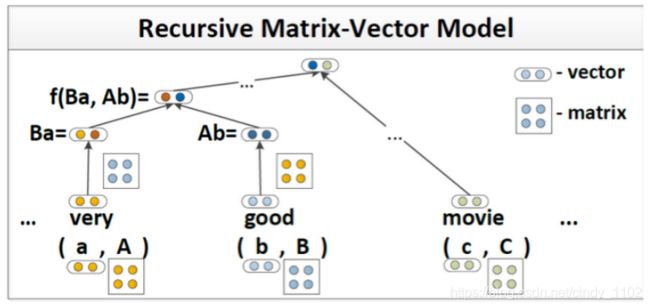
现在扩大单词表示，不仅包括一个单词向量，还包括一个单词矩阵。因此，单词 “very” 将有一个词向量 $v_{very}\in {\mathbb{R}}^d$ 和一个词矩阵$V_{very}\in {\mathbb{R}}^{d\ast d}$。这样不仅能够表达单词自身的意思，还能学习单词 “修饰” 其他单词的方式，“矩阵” 使后者成为可能。将两个单词a和b输入RNN，取它们的单词矩阵A和B，将输入向量x表示为向量Ab和Ba的串联。比如 “very”，$V_{very}$可以是单位矩阵乘以任意大于1的标量。它可以将任何相邻的词向量乘以这个数。新的单词表示开拓了特征空间，可以更好地表达单词彼此修饰的方式。

对模型误差进行观察，发现即使是MV-RNN也不能表达某些关系。观察到三类错误：

1. Negated Positives。当有一个积极的词汇时，另外一个词将其变成了消极的，模型无法捕捉到这个强大到足以翻转整个句子情绪的词。如下图所示，将单词“most”转换为“least”应该会翻转整个句子的情绪，但是MV-RNN没有成功地捕捉到这一点。
   
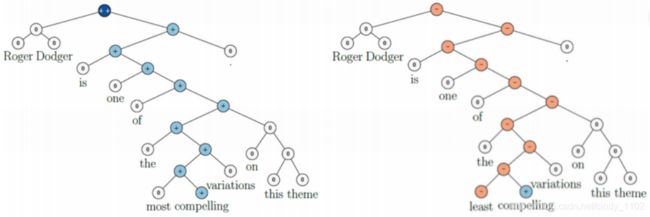
2. Negated Negatives。有时说某事不坏，或者不枯燥，如下图所示，MV-RNN无法识别出 “不” 这个会使情绪从消极变为中性的词。
   
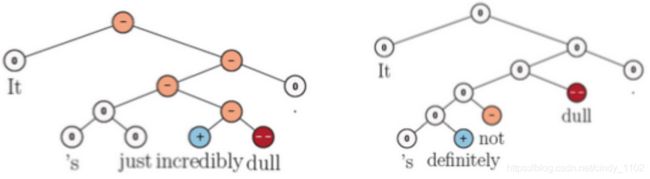
3. X but Y conjunction。这里的X可能是负的，但如果Y是正的，那么模型对句子的情感输出应该是正的，MV-RNNs无法对此进行区分。
   

因此，需要找到一种更具表现力的组合算法，能够完全捕捉这些类型的高级组合。

RNTNs (Recursive Neural Tensor Network)

本节讨论的最后一个RNN是迄今为止在上述三种错误类型上最成功的。递归神经张量网络（RNTN）消除了词矩阵的概念以及传统仿射变换的pre-tanh/sigmoid概念。为了组成两个单词向量或短语向量，再次将它们串联形成一个向量 $\in {\mathbb{R}}^{2d}$，但没有先把它放入仿射函数，而是先放入一个二次方程，然后进行非线性变换，比如$$h^{(1)}=tanh(x^{T}Vx+Wx)$$注意 $V\in {\mathbb{R}}^{2d\ast 2d\ast d}$是一个三阶张量。计算$x^{T}V[i]x,\forall i\in [1,2，\dots d]$张量的切片，输出向量 $\in {\mathbb{R}}^d$。然后加上Wx 经过一个非线性函数。这个二次函数可以允许字向量之间的乘法交互。

成分句法分析

前面的笔记中介绍过依存关系分析，即通过在单词及其依赖项之间建立二进制非对称关系，显示哪个单词依赖于哪个单词。现在关注成分句法分析，将单词变成嵌套形式。

成分句法分析是将一段文本(例如一个句子)分成子短语的一种方法 (也称为“短语结构分析”) 其目标之一是识别文本中的成分，这些成分在文本信息提取时非常有用。通过分析句子成分，可以生成语法正确的相似句子。

成分

在句法分析中，成分可以是一个单词或短语，作为层次结构中的一个单元。短语是由两个或以上的单词组成的序列，围绕头部词汇项，在句子中作为一个单元。作为短语的一组词应该在句子中发挥特定的作用。此外，该组词可以整体移动或替换，句子依旧保持流利和语法正确。

例如，下面的句子包含名词短语:“wonderful CS224N”。

• I want to be enrolled in the wonderful CS224N !
  可以把整个短语移到前面来重写这个句子，如下所示。
• The wonderful CS224N I want to be enrolled in !
  或者这个短语可以替换成一个功能和意义相似的组成部分，比如"great CS course in Stanford about NLP and Deep Learning"
• I want to be enrolled in the great CS course in Stanford about NLP
  and Deep Learning !

对于成分分析，基本子句结构被理解为主语(名词短语NP)和谓语(动词短语VP)的二元划分。对于句子中的每个元素，树结构中都有一个或多个节点。

• S -> NP VP

事实上，解析过程说明了某些类似的规则。从句子符号S开始推导，依次应用短语结构规则，最后用替换规则代替抽象符号的实际单词。根据提取规则可以生成相似的句子。如果规则正确，那么以这种方式产生的任何句子都应该在语法上正确。然而，生成的句子在语法上可能是正确的，但在语义上可能是无意义的，比如：Colorless green ideas sleep furiously

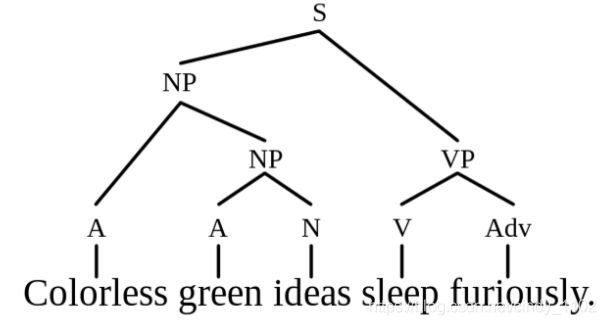
成分解析树

在自然语言中各个成分很可能彼此嵌套在一起。因此，短语的自然表示形式是树。通常使用成分解析树来显示解析过程。树中的非终端被标记为短语的类型(如名词短语)，终端是句子中的准确单词。以John hit the ball为例，句法结构如下图所示。

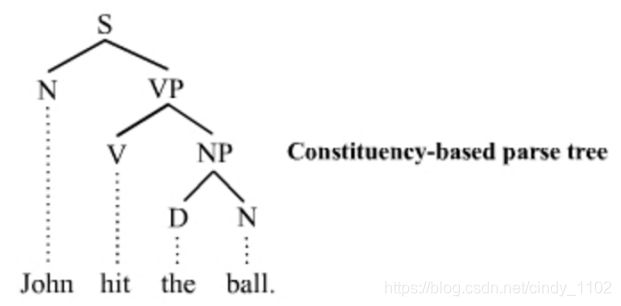
解析树从表示整个句子的根S开始，到表示句子中的每个单词的每个叶子节点结束。使用以下缩写：

• S代表句子，最高级的结构。
• NP代表名词短语，包括句子的主语和宾语。
• VP代表动词短语，用作谓语。
• V代表动词。
• D代表限定词，如定冠词the
• N代表名词

Tips：本节笔记中提到的RNNs都依赖于这样的初始解析。如果使用的是循环网络而短语的上下文都在右边，只在最后一个时间步上应用Softmax，那么最后几个单词将对输出产生不成比例的巨大影响，例如情绪分类。前一篇笔记所述的卷积神经网络可以用于解决这个问题。