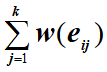图的计算(2):带权图的最短路径
带权图(weighted digraph)
设G=(V,E)是一简单图。称一元函数 w:E®R+ 为图G 的权函数,使得 对于每一条边eÎE,均有一正实数w(e)ÎR+与之对应,称图G 为带有权w的图,简称为带权图。并记为G=(V,E, w)。
最短路(shortest path)
设G=(V,E,w)是一带权图。
(1)设P=(ei1, ei2,¼, eik)是G中的一条路。则路P的路长
(2)从结点u到结点v的最短路P0是满足下述条件的路:
w(P0)=min{ w(P) êP为从u到v的路} 。
注:当带权图中各边的权值都为1时,则路长的定义就蜕化为§3一般图的路长定义了。
E.W.Dijkstra算法(1959):
算法的目标是求出带权图G中从结点v0到结点vn的最短路。
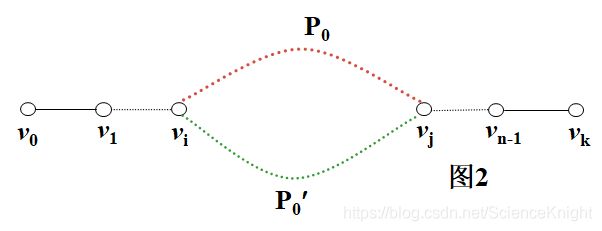
特别地,最短路P0 的任一真前缀(v0, v1, v2,¼, vk)(k< n)也是最短的。
否则,将局部段换为最短的,则可得一比P0更短的路P0¢,这与已知P0是最短路矛盾。
No1.P:={v0} ; T :=V\{v0} ; /*设定P-T界面*/
d(v0) :=0;(tT)(d(t) := ) ;
/*做圆标号(用一重for循环可实现) */
p := v0 ; mark(v0) := d(v0) ; /*做方标号*/
No2. (tT)(d(t) := min{d(t) , d(p)+w(p,t)}) ;
/*按离界面最近方向修改圆标 号(用一重for循环可实现)*/
(t0T)(tT)(d(t0) d(t)) ;
/*寻求T 中圆标号最小的结点t0 (用一重for循环及if比较可实现)*/
No3.P:=P{t0} ; T :=T\{t0} ; /*修改P-T界面*/
p := t0 ; mark(t0) := d(t0) ; /*改圆为方*/
No4.if t0 = vn then goto exit ;
else goto No2 ;
将带权图G的结点集V分成两部分:一部分称为具有P标号(方标号)的集合;另一部分称为具有T标号(圆标号)的集合。所谓结点vi的P标号是指从v0到vi的最短路的路长;而结点vi的T标号是指从v0到vi的某条路径的长度。
Dijkstra算法首先将v0取为 P 标号结点;其余的结点均取为T标号结点;然后按离P-T界面最近方向逐步地将具有T标号的结点改为P标号结点。当结点vn也被改为P标号结点时,也就求出了从(起始)结点v0到各个结点vi的最短路长;尤其是求出了从(起始)结点v0到(终结)结点vn的最短路长。
程序计算法:
1. P={v0};T={v1,v2,v3,v4,v5};
d(v0)=0; d(v1)=d(v2)=d(v3)=d(v4)=d(v5)=; p=v0;
2. d(v1)=1 ; d(v2)=4 ; d(v3)=d(v4)=d(v5)=;
t0 =v1;
3. P={v0,v1}; T={v2, v3,v4,v5}; p=v1;
4. t0v5; go to 2;
2. d(v2)=3 ; d(v3)=8 ; d(v4)=6 ; d(v5)= ;
t0=v2 ;
3. P={v0,v1,v2}; T={v3,v4,v5}; p=v2;
4. t0 v5 ; go to 2 ;
2. d(v3)=8 ; d(v4)=4 ; d(v5)= ;
t0 = v4 ;
3. P={v0,v1,v2, v4};T={v3, v5}; p=v4;
4. t0 v5 ; go to 2;
2. d(v3)=7; d(v5)=10;
t0= v3;
3. P={v0, v1, v2, v4, v3}; T={v5} ; p=v3;
4. t0v5 ; go to 2;
2. d(v5)=9;
t0=v5 ;
3. P={v0,v1,v2,v4,v3,v5} ; T={ }; p=v5;
4. t0=v5 ;exit ;
注: ·显然,图上作业法的优点是直观,缺点是画图麻烦。 可以将No2步和No3步的图合为一个图,以达简化的目地(例如图3和图4可合并成一个图);
·显然,程序计算法的优点是简便、机械,缺点是缺乏直观性、计算出错不易检查。
·Dijkstra算法能够一次性的求出从起点v0到带权图G中其余每一个结点的最短路长(就是各结点方标号中的数值)。
·Dijkstra算法没有直接给出从起点v0到带权图G中其余各结点的最短路。因此,要直接给出从起点v0到带权图G中其余各结点的最短路,需要修改Dijkstra算法,或者①给其嵌入记忆系统(用表结构或仅记前一个结点);或者②给其增加回溯功能。
Dijkstra算法的特点:
·Dijkstra算法是沿着P-T界面(按离界面最近方向)向前推进的;而不是沿着最短路向前推进的。
Dijkstra算法的计算工作量主要是集中在No2。在úPê=k , úTê=n-k(0£k £ n-1)时,当P再增加一个结点,需进入一次循环:
从表1可得Dijkstra算法的(时间)复杂性是n2级的; (空间)复杂性也是n2级的。
|
|
加法(次) |
比较(次) |
存贮量(单元) |
| 算一个结点 |
1 |
1 |
1 |
| 算一次循环 |
n-k-1 |
2(n-k-1) |
1 |
| 完成计算 |
n(n-1) |
|