路径规划算法学习Day5

---

原理回顾

路径规划算法学习Day4-Astar算法

---

一、A* 算法评价函数

评价函数:f(n)=h(n)+g(n);
A* 可以看作Dijkstar和贪婪算法的结合，Dijkstar在规划中注重的是当前节点到起点的总代价值。而贪婪算法注重的是当前节点到终点的总代价值。
所以将评价函数定义为f(n),h(n)则为贪婪算法的权重代价，g(n)为Dijkstar的权重代价。
根据评价函数f(n)，A* 函数就会有目的性的去规划路径。

二、曼哈顿距离（Manhattan Distance）

出租车几何或曼哈顿距离（Manhattan Distance）是由十九世纪的赫尔曼·闵可夫斯基所创词汇 ，是种使用在几何度量空间的几何学用语，用以标明两个点在标准坐标系上的绝对轴距总和。

2.1、名词解释

图1中红线代表曼哈顿距离，绿色代表欧氏距离，也就是直线距离，而蓝色和黄色代表等价的曼哈顿距离。曼哈顿距离——两点在南北方向上的距离加上在东西方向上的距离，即d(i,j)=|xi-xj|+|yi-yj|。对于一个具有正南正北、正东正西方向规则布局的城镇街道，从一点到达另一点的距离正是在南北方向上旅行的距离加上在东西方向上旅行的距离，因此，曼哈顿距离又称为出租车距离。曼哈顿距离不是距离不变量，当坐标轴变动时，点间的距离就会不同。曼哈顿距离示意图在早期的计算机图形学中，屏幕是由像素构成，是整数，点的坐标也一般是整数，原因是浮点运算很昂贵，很慢而且有误差，如果直接使用AB的欧氏距离(欧几里德距离：在二维和三维空间中的欧氏距离的就是两点之间的距离），则必须要进行浮点运算，如果使用AC和CB，则只要计算加减法即可，这就大大提高了运算速度，而且不管累计运算多少次，都不会有误差。

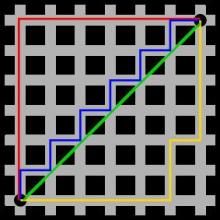
我们可以定义曼哈顿距离的正式意义为L1-距离或城市区块距离，也就是在欧几里德空间的固定直角坐标系上两点所形成的线段对轴产生的投影的距离总和。
例如在平面上，坐标(x1,y1)的i点与坐标(x2,y2)的j点的曼哈顿距离为：
d(i,j)=|X1-X2|+|Y1-Y2|.
此原理参考：曼哈顿距离

2.2、其它启发函数

当然，启发函数不单单曼哈顿距离一种，常见的还有欧式距离、切比雪夫距离等等。
欧式距离
切比雪夫距离

二、A* 算法matlab完全实现

3.1、地图创建

见路径规划算法学习Day3

3.2、A*算法matlab主程序

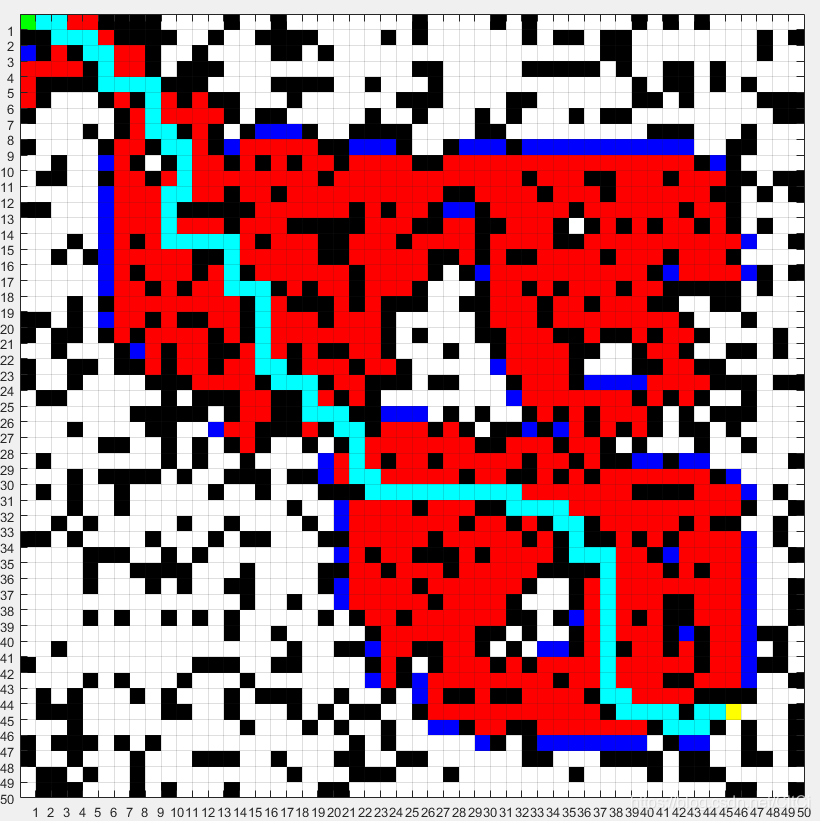
load('Map50.mat');    
start_node = [1, 1];   
dest_node  = [45, 46]; 
figure(1);
[path, iterations] = Astar1(map, start_node, dest_node);

3.3、A*算法matlab主程序

function [path,iterations]=Astar1(Map,origin,destination)
Heuristic_ratio = 1;%启发式函数比例
iterations=0;%记录迭代次数
%图像颜色给定
white = [1,1,1];%1
black = [0,0,0];%2
green = [0,1,0];%3
yellow = [1,1,0];%4
red = [1,0,0];%5
blue = [0,0,1];%6
cyan = [0,1,1];%7
color_list = [white; black; green; yellow; red; blue; cyan];
colormap(color_list);
Obstacle = 2;%障碍
Origin = 3;%开始
Destination = 4;%终点
Finished = 5;%完成搜索
Unfinished = 6;%未完成搜索
Path = 7;%路径

[rows, cols]=size(Map);
%创建地图
logical_map = logical(Map);
map = zeros(rows,cols);
map(logical_map) = 2;%Barrier
map(~logical_map) = 1;%free
%list----g
node_g_list = Inf(rows, cols);
node_g_list(origin(1), origin(2)) = 0;
%list----f
node_f_list = Inf(rows, cols);
node_f_list(origin(1), origin(2)) = Heuristic(origin, destination, Heuristic_ratio);
% 创建父节点列表
parent_list = zeros(rows,cols);

destination_index = sub2ind(size(Map), destination(1), destination(2));
origin_index = sub2ind(size(Map), origin(1), origin(2));
Open_list = [origin_index];
plan_succeeded = false;
%迭代循环
while 1
    iterations = iterations+1;
    map(origin(1), origin(2)) = Origin;
    map(destination(1), destination(2)) = Destination;
   
    [min_node_cost, current_node_index] = min(node_f_list(:));
	if(min_node_cost == inf || current_node_index == destination_index)
		plan_succeeded = true;
		break;
    end
    node_f_list(current_node_index) = inf;
    map(current_node_index) = Finished;
	[i,j] = ind2sub(size(map), current_node_index);
    for k = 0:3	% four direction
                if(k == 0)
                    adjacent_node = [i-1,j];
                     elseif (k == 1)
                    adjacent_node = [i+1,j];
                    elseif (k == 2)
                        adjacent_node = [i,j-1];
                    elseif(k == 3)
                    adjacent_node = [i,j+1];
                end
    if((adjacent_node(1) > 0 && adjacent_node(1) <= rows) && (adjacent_node(2) > 0 && adjacent_node(2) <= cols)) %保证搜索不超过地图界限
            if(map(adjacent_node(1),adjacent_node(2)) ~= Obstacle && map(adjacent_node(1),adjacent_node(2)) ~= Finished)
                if(node_g_list(adjacent_node(1),adjacent_node(2)) > min_node_cost + 1 )
                    node_g_list(adjacent_node(1),adjacent_node(2)) = node_g_list(current_node_index) + 1;                 
                    node_f_list(adjacent_node(1),adjacent_node(2)) = node_g_list(adjacent_node(1),adjacent_node(2)) + Heuristic(adjacent_node, destination, Heuristic_ratio);                  
                    if(map(adjacent_node(1),adjacent_node(2)) == Origin)
                        parent_list(adjacent_node(1),adjacent_node(2)) = 0;	%如果邻接节点是原点，则设置父节点为0。.
                    else
                        parent_list(adjacent_node(1),adjacent_node(2)) = current_node_index;
                        %设置父当前节点索引
                    end
                    if(map(adjacent_node(1),adjacent_node(2)) ~= Unfinished)
                        map(adjacent_node(1),adjacent_node(2)) = Unfinished;	
                        %将相邻节点标记为未完成
                    end
                end
            end
        end
	end
end

if(plan_succeeded)
	path = [];
	node = destination_index;
	while(parent_list(node) ~= 0)
		path = [parent_list(node), path];
		node = parent_list(node);
    end
    
	for k = 2:size(path,2)
		map(path(k)) = 7;
		image(0.5,0.5,map);
		grid on;
        set(gca,'xtick',1:1:rows);
        set(gca,'ytick',1:1:rows);
		axis image;
		drawnow;
	end
else
	path = [];
end
end

四、A* 算法50*50地图演示

五、总结

此文为A*算法的完全实现，有问题请评论，欢迎大家查阅指正。