【路径规划】华为杯:基于matlab 无人机优化运用于抢险救灾【Matlab 033期】
一、背景
以2017年华为杯研究生数学建模比赛A题(无人机在抢险救灾中的优化运用)为例,讲解蚁群算法在求解最优路径问题中的应用,我们将问题进行了简化,描述如下:
无人机从某一个基地出发,途径所有救援点,然后回到基地(每个点只经过一次),求解最佳行驶路径。
基地和所有救援点的散点图如图1所示。
蚁群算法是寻求优化路径的一种算法,这种算法的思想起源于蚂蚁在寻求事物过程中的路径,这种算法在本质上属于一种启发式全局优化算法,具有信息正反馈、分布计算和启发式搜索的特点。蚁群算法采用的规则主要为环境信息、避障规则、移动规则、散发信息素规则等。蚁群算法主要应用在组合优化问题上,同时其在网络路由中应用也越来越广泛。
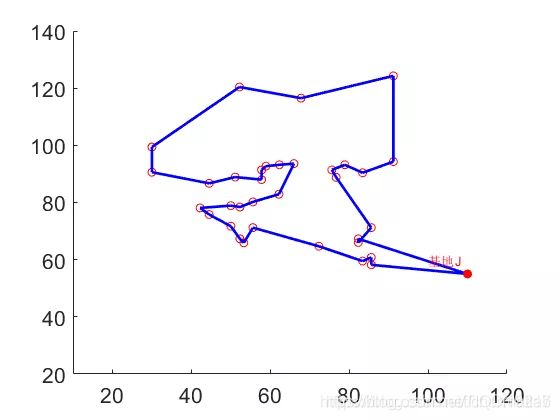
最终使用蚁群算法得到的救援路线如图2所示:
二、源代码
我们提供了可运行的代码,并添加了注释,大家可自行去了解该算法的精髓。代码包含三个部分,主函数mainfun.m调用Antcolonyalgorithm.m和flightRoute.m. Antcolonyalgorithm.m用于实现蚁群算法,flightRoute.m用于画飞行路线。
function mainfun()
% 位点坐标
position=[ 91.2000 94.3000
83.4000 90.4000
76.7000 88.8000
57.8000 91.4000
75.6000 91.4000
57.8000 88.0000
51.1000 88.9000
30.0000 90.6000
30.0000 99.4000
42.2000 78.1000
58.9000 92.7000
62.3000 93.2000
50.0000 78.9000
44.5000 86.7000
55.6000 71.2000
52.3000 67.3000
72.3000 64.7000
82.3000 66.0000
85.6000 71.2000
82.3000 67.3000
85.6000 58.2000
85.6000 60.8000
83.4000 59.5000
50.0000 71.7000
52.3000 78.4000
44.5000 75.8000
66.0000 93.6000
62.2000 82.9000
78.9000 93.2000
67.8000 116.5000
52.2000 120.4000
55.6000 80.2000
91.2000 124.3000
53.3000 65.9000
110.0000 55.0000];
% 所有点的散点图
figure
scatter(position(:,1),position(:,2),'ro');
hold on
axis([10,120,20,140])
plot(110,55,'ro','MarkerFaceColor','r')
text(100,60,'基地J','Color','r')
set(gca,'FontSize',16)
% 蚁群算法
[~,L_best,L_ave,Shortest_Route,Shortest_Length]=Antcolonyalgor
figure
plot(L_best,'b','LineWidth',2)
hold on
plot(L_ave,'b','LineWidth',2)
xlabel('迭代次数')
ylabel('平均距离和最短距离')
set(gca,'FontSize',16)
end
蚁群算法函数——
function [R_best,L_best,L_ave,Shortest_Route,Shortest_Length]=Antcolonyalgorithm(C,NC_max,m,Alpha,Beta,Rho,Q)
% 输入输出说明
% C城市的坐标
% NC_max 最大迭代次数
% m 蚂蚁个数
% Rho 信息素蒸发系数
% Q 信息素增加强度系数
% R_best 最佳路线
% L_best 最佳路线的长度
% Alpha 信息素重要程度
% Beta 启发式因子重要程度
%变量初始化
n=size(C,1);
D=zeros(n,n);
for i=1:n
for j=1:n
if i~=j
D(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5;
else
D(i,j)=eps;
end
D(j,i)=D(i,j);
end
end
Eta=1./D;
Tau=ones(n,n);
Tabu=zeros(m,n);
NC=1;
R_best=zeros(NC_max,n);
L_best=inf.*ones(NC_max,1);
L_ave=zeros(NC_max,1);
while NC<=NC_max
Randpos=[];
for i=1:(ceil(m/n))
Randpos=[Randpos,randperm(n)];
end
Tabu(:,1)=(Randpos(1,1:m))';
for j=2:n
for i=1:m
visited=Tabu(i,1:(j-1));
J=zeros(1,(n-j+1));
P=J;
Jc=1;
for k=1:n
if isempty(find(visited==k, 1))
J(Jc)=k;
Jc=Jc+1;
end
end
if NC>=2
Tabu(1,:)=R_best(NC-1,:);
end
L=zeros(m,1);
for i=1:m
R=Tabu(i,:);
for j=1:(n-1)
L(i)=L(i)+D(R(j),R(j+1));
end
L(i)=L(i)+D(R(1),R(n));
end
L_best(NC)=min(L);
pos=find(L==L_best(NC));
R_best(NC,:)=Tabu(pos(1),:);
L_ave(NC)=mean(L);
NC=NC+1;
%更新信息素
Delta_Tau=zeros(n,n);
for i=1:m
for j=1:(n-1)
Delta_Tau(Tabu(i,j),Tabu(i,j+1))=Delta_Tau(Tabu(i,j),Tabu(i,j+1))+Q/L(i);
end
Delta_Tau(Tabu(i,n),Tabu(i,1))=Delta_Tau(Tabu(i,n),Tabu(i,1))+Q/L(i);
end
Tau=(1-Rho).*Tau+Delta_Tau;
%禁忌表清零
Tabu=zeros(m,n);
end
%输出结果
Pos=find(L_best==min(L_best));
Shortest_Route=R_best(Pos(1),:);
Shortest_Length=L_best(Pos(1));
end
画路线图的函数,输入为位点坐标和路径——
function flightRoute(C,Rou)
Num=length(Rou);
scatter(C(:,1),C(:,2));
hold on
plot([C(Rou(1),1),C(Rou(Num),1)],[C(Rou(1),2),C(Rou(Num),2)],'r','LineWidth',3)
hold on
for ii=2:Num
plot([C(Rou(ii-1),1),C(Rou(ii),1)],[C(Rou(ii-1),2),C(Rou(ii),2)],'r','LineWidth',3)
hold on
end
end
四、备注
完整代码或者代写添加QQ912100926。
往期回顾>>>>>>
【路径规划】粒子群优化算法之三维无人机路径规划【Matlab 012期】
【路径规划】遗传算法之多物流中心的开放式车辆路径规划【Matlab 013期】
【路径规划】粒子群算法之机器人栅格路径规划【Matlab 014期】
【路径规划】蚁群算法之求解最短路径【Matlab 015期】
【路径规划】免疫算法之物流中心选址【Matlab 016期】
【路径规划】人工蜂群之无人机三维路径规划【Matlab 017期】
【路径规划】遗传算法之基于栅格地图机器人路径规划【Matlab 018期】
【路径规划】蚁群算法之多无人机攻击调度【Matlab 019期】
【路径规划】遗传算法之基于栅格地图的机器人最优路径规划【Matlab 020期】
【路径规划】遗传算法之考虑分配次序的多无人机协同目标分配建模【Matlab 021期】
【路径规划】蚁群算法之多中心vrp问题【Matlab 022期】
【路径规划】蚁群算法之求解带时间窗的多中心VRP【Matlab 023期】
【路径规划】遗传算法之多中心VRP求解【Matlab 024期】
【路径规划】模拟退火之求解VRP问题【Matlab 025期】
【路径规划】A星之栅格路径规划【Matlab 026期】
【路径规划】基于一种带交叉因子的双向寻优粒子群栅格地图路径规划【Matlab 027期】
【路径规划】【TSP】蚁群算法之求解TSP问题含GUI【Matlab 028期】
【路径规划】蚁群算法之栅格地图路径规划【Matlab 029期】
【路径规划】遗传算法之旅行商 TSP 【Matlab 030期】
【路径规划】模拟退火算法之旅行商 TSP 问题【Matlab 031期】
【路径规划】蚁群算法之智能车路径规划【Matlab 032期】