Leetcode题解---杂题
目录
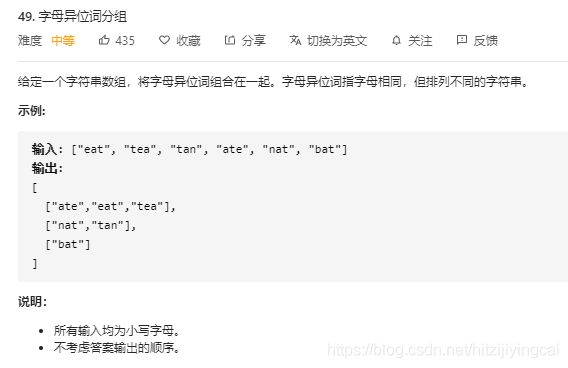
49. 字母异位词分组
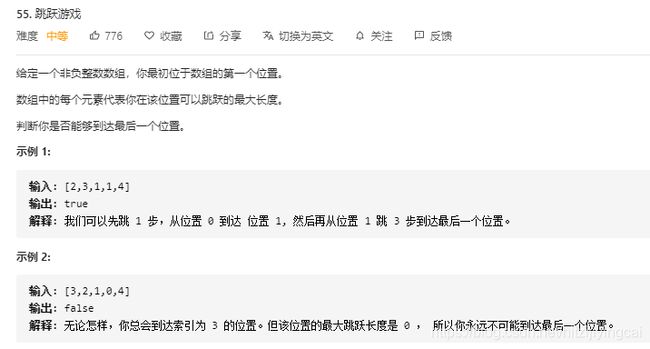
55. 跳跃游戏
56. 合并区间
75. 颜色分类
78. 子集
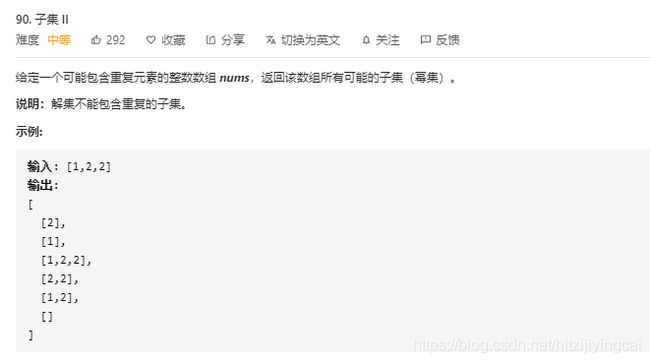
90. 子集 II
128. 最长连续序列
136. 只出现一次的数字
139. 单词拆分
146. LRU缓存机制
155. 最小栈
169. 多数元素
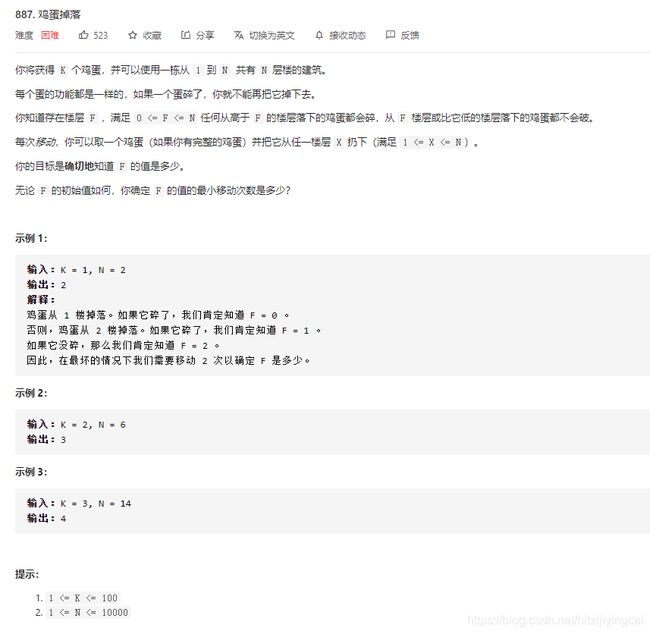
887. 鸡蛋掉落
具体如下:
49. 字母异位词分组
class Solution:
def groupAnagrams(self, strs: List[str]) -> List[List[str]]:
dict = {}
for item in strs:
key = tuple(sorted(item))
dict[key] = dict.get(key, []) + [item]
return list(dict.values())55. 跳跃游戏
思路:尽可能到达最远位置(贪心)。
如果能到达某个位置,那一定能到达它前面的所有位置。
方法:初始化最远位置为 0,然后遍历数组,如果当前位置能到达,并且当前位置+跳数>最远位置,就更新最远位置。最后比较最远位置和数组长度。
复杂度:时间复杂度 O(n),空间复杂度 O(1)。
初始写法:
class Solution:
def canJump(self, nums) :
max_i = 0 #初始化当前能到达最远的位置
for i, jump in enumerate(nums): #i为当前位置,jump是当前位置的跳数
if max_i>=i and i+jump>max_i: #如果当前位置能到达,并且当前位置+跳数>最远位置
max_i = i+jump #更新最远能到达位置
return max_i>=i
改进写法:
class Solution:
def canJump(self, nums: List[int]) -> bool:
if nums == [0]: return True
maxDist = 0
end_index = len(nums)-1
for i, jump in enumerate(nums):
if maxDist >= i and i+jump > maxDist:
maxDist = i+jump
if maxDist >= end_index:
return True
return False56. 合并区间
class Solution:
def merge(self, intervals: List[List[int]]) -> List[List[int]]:
intervals.sort(key=lambda x: x[0])
merged = []
for interval in intervals:
# 如果列表为空,或者当前区间与上一区间不重合,直接添加
if not merged or merged[-1][1] < interval[0]:
merged.append(interval)
else:
# 否则的话,我们就可以与上一区间进行合并
merged[-1][1] = max(merged[-1][1], interval[1])
return merged75. 颜色分类
我们用三个指针(p0, p2 和curr)来分别追踪0的最右边界,2的最左边界和当前考虑的元素。
本解法的思路是沿着数组移动 curr 指针,若nums[curr] = 0,则将其与 nums[p0]互换;若 nums[curr] = 2 ,则与 nums[p2]互换。
算法
初始化0的最右边界:p0 = 0。在整个算法执行过程中 nums[idx < p0] = 0.
初始化2的最左边界 :p2 = n - 1。在整个算法执行过程中 nums[idx > p2] = 2.
初始化当前考虑的元素序号 :curr = 0.
While curr <= p2 :
若 nums[curr] = 0 :交换第 curr个 和 第p0个 元素,并将指针都向右移。
若 nums[curr] = 2 :交换第 curr个和第 p2个元素,并将 p2指针左移 。
若 nums[curr] = 1 :将指针curr右移。
class Solution {
public:
void sortColors(vector& nums) {
// 对于所有 idx < p0 : nums[idx < p0] = 0
// curr 是当前考虑元素的下标
int p0 = 0, curr = 0;
// 对于所有 idx > p2 : nums[idx > p2] = 2
int p2 = nums.size() - 1;
while (curr <= p2) {
if (nums[curr] == 0) {
swap(nums[curr++], nums[p0++]);
}
else if (nums[curr] == 2) {
swap(nums[curr], nums[p2--]);
}
else curr++;
}
}
}; class Solution:
def sortColors(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
'''
荷兰三色旗问题解
'''
# 对于所有 idx < p0 : nums[idx < p0] = 0
# curr是当前考虑元素的下标
p0 = curr = 0
# 对于所有 idx > p2 : nums[idx > p2] = 2
p2 = len(nums) - 1
while curr <= p2:
if nums[curr] == 0:
nums[p0], nums[curr] = nums[curr], nums[p0]
p0 += 1
curr += 1
elif nums[curr] == 2:
nums[curr], nums[p2] = nums[p2], nums[curr]
p2 -= 1
else:
curr += 178. 子集
回溯法:
定义一个回溯方法 backtrack(first, curr),第一个参数为索引 first,第二个参数为当前子集 curr。
如果当前子集构造完成,将它添加到输出集合中。
否则,从 first 到 n 遍历索引 i。
将整数 nums[i] 添加到当前子集 curr。
继续向子集中添加整数:backtrack(i + 1, curr)。
从 curr 中删除 nums[i] 进行回溯。
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
def backtrack(first = 0, curr = []):
# if the combination is done
if len(curr) == k:
output.append(curr[:])
for i in range(first, n):
# add nums[i] into the current combination
curr.append(nums[i])
# use next integers to complete the combination
backtrack(i + 1, curr)
# backtrack
curr.pop()
output = []
n = len(nums)
for k in range(n + 1):
backtrack()
return output递归:
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
n = len(nums)
output = [[]]
for num in nums:
output += [curr + [num] for curr in output]
return output90. 子集 II
相对于78题只需要去重即可,去重可以在搜索函数中加入条件语句,continue即可。
class Solution:
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
nums = sorted(nums)
n = len(nums)
res = []
def back_func(start=0, temp=[]):
res.append(temp[:])
for i in range(start, n):
if i > start and nums[i] == nums[i-1]:
continue
temp.append(nums[i])
back_func(i+1, temp)
temp.pop()
back_func()
return resclass Solution {
public:
vector> ans;
vector cur;
vector v;
void dfs(int idx) {
ans.push_back(cur);
if(idx == v.size()) {
return;
}
for(int i=idx; i idx && v[i] == v[i-1]) continue;
cur.push_back(v[i]);
dfs(i+1);
cur.pop_back();
}
}
vector> subsetsWithDup(vector& nums) {
sort(nums.begin(), nums.end());
v = nums;
dfs(0);
return ans;
}
}; 128. 最长连续序列
class Solution {
public:
int longestConsecutive(vector& nums) {
unordered_set num_set;
for (const int& num : nums) {
num_set.insert(num);
}
int longestStreak = 0;
for (const int& num : num_set) {
if (!num_set.count(num - 1)) {
int currentNum = num;
int currentStreak = 1;
while (num_set.count(currentNum + 1)) {
currentNum += 1;
currentStreak += 1;
}
longestStreak = max(longestStreak, currentStreak);
}
}
return longestStreak;
}
};
class Solution:
def longestConsecutive(self, nums: List[int]) -> int:
longest_streak = 0
num_set = set(nums)
for num in num_set:
if num - 1 not in num_set:
current_num = num
current_streak = 1
while current_num + 1 in num_set:
current_num += 1
current_streak += 1
longest_streak = max(longest_streak, current_streak)
return longest_streak136. 只出现一次的数字
法1:位运算
##Python代码
class Solution:
def singleNumber(self, nums: List[int]) -> int:
return reduce(lambda x, y: x ^ y, nums)
class Solution {
public:
int singleNumber(vector& nums) {
int ret = 0;
for (auto e: nums) ret ^= e;
return ret;
}
};
法2:使用collections库
class Solution:
def singleNumber(self, nums: List[int]) -> int:
import collections
setting = collections.Counter(nums)
for k,v in setting.items():
if v == 1:
return k
break139. 单词拆分
class Solution:
def wordBreak(self, s: str, wordDict: List[str]) -> bool:
n=len(s)
dp=[False]*(n+1)
dp[0]=True
for i in range(n):
for j in range(i+1,n+1):
if(dp[i] and (s[i:j] in wordDict)):
dp[j]=True
return dp[-1]146. LRU缓存机制
# Your LRUCache object will be instantiated and called as such:
# obj = LRUCache(capacity)
# param_1 = obj.get(key)
# obj.put(key,value)
class DLinkedNode:
def __init__(self, key=0, value=0):
self.key = key
self.value = value
self.prev = None
self.next = None
class LRUCache:
def __init__(self, capacity: int):
self.cache = dict()
# 使用伪头部和伪尾部节点
self.head = DLinkedNode()
self.tail = DLinkedNode()
self.head.next = self.tail
self.tail.prev = self.head
self.capacity = capacity
self.size = 0
def get(self, key: int) -> int:
if key not in self.cache:
return -1
# 如果 key 存在,先通过哈希表定位,再移到头部
node = self.cache[key]
self.moveToHead(node)
return node.value
def put(self, key: int, value: int) -> None:
if key not in self.cache:
# 如果 key 不存在,创建一个新的节点
node = DLinkedNode(key, value)
# 添加进哈希表
self.cache[key] = node
# 添加至双向链表的头部
self.addToHead(node)
self.size += 1
if self.size > self.capacity:
# 如果超出容量,删除双向链表的尾部节点
removed = self.removeTail()
# 删除哈希表中对应的项
self.cache.pop(removed.key)
self.size -= 1
else:
# 如果 key 存在,先通过哈希表定位,再修改 value,并移到头部
node = self.cache[key]
node.value = value
self.moveToHead(node)
def addToHead(self, node):
node.prev = self.head
node.next = self.head.next
self.head.next.prev = node
self.head.next = node
def removeNode(self, node):
node.prev.next = node.next
node.next.prev = node.prev
def moveToHead(self, node):
self.removeNode(node)
self.addToHead(node)
def removeTail(self):
node = self.tail.prev
self.removeNode(node)
return node
155. 最小栈
算法
我们只需要设计一个数据结构,使得每个元素 a 与其相应的最小值 m 时刻保持一一对应。因此我们可以使用一个辅助栈,与元素栈同步插入与删除,用于存储与每个元素对应的最小值。
当一个元素要入栈时,我们取当前辅助栈的栈顶存储的最小值,与当前元素比较得出最小值,将这个最小值插入辅助栈中;
当一个元素要出栈时,我们把辅助栈的栈顶元素也一并弹出;
在任意一个时刻,栈内元素的最小值就存储在辅助栈的栈顶元素中。
class MinStack:
def __init__(self):
"""
initialize your data structure here.
"""
self.stack = []
self.min_stack = [math.inf]
def push(self, x: int) -> None:
self.stack.append(x)
self.min_stack.append(min(x, self.min_stack[-1]))
def pop(self) -> None:
self.stack.pop()
self.min_stack.pop()
def top(self) -> int:
return self.stack[-1]
def getMin(self) -> int:
return self.min_stack[-1]
# Your MinStack object will be instantiated and called as such:
# obj = MinStack()
# obj.push(x)
# obj.pop()
# param_3 = obj.top()
# param_4 = obj.getMin()169. 多数元素
法一:排序
class Solution:
def majorityElement(self, nums):
nums.sort()
return nums[len(nums)//2]
法二:
class Solution:
def majorityElement(self, nums):
counts = collections.Counter(nums)
return max(counts.keys(), key=counts.get)887. 鸡蛋掉落
有一个视频讲解:https://www.bilibili.com/video/BV1KE41137PK
class Solution:
def superEggDrop(self, K: int, N: int) -> int:
memo = {}
def dp(k, n):
if (k, n) not in memo:
if n == 0:
ans = 0
elif k == 1:
ans = n
else:
lo, hi = 1, n
# keep a gap of 2 X values to manually check later
while lo + 1 < hi:
x = (lo + hi) // 2
t1 = dp(k-1, x-1)
t2 = dp(k, n-x)
if t1 < t2:
lo = x
elif t1 > t2:
hi = x
else:
lo = hi = x
ans = 1 + min(max(dp(k-1, x-1), dp(k, n-x))
for x in (lo, hi))
memo[k, n] = ans
return memo[k, n]
return dp(K, N)